绝密★启用前(命题人:荣培元 审题人:杨少平)
湖北省荆州中学2009届高三5月模拟考试
数 学(文史类)
说明:本试卷共4面,满分150分,考试时间120分钟
第 Ⅰ 卷(共50分)
一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1.设集合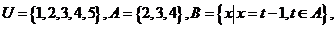 则
则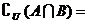 ( )
( )
A.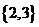 B.
B.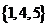 C.
C.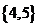 D.
D.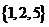
2.已知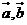 都是非零向量,命题
都是非零向量,命题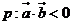 ,命题
,命题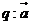 与
与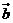 夹角为钝角.则
夹角为钝角.则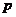 是
是 成立的( )
成立的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.前段时间,三鹿奶粉添加三聚氰胺的问题引起全社会的关注.某市质量监督局为了保证人民的饮食安全,要对超市中奶粉的质量进行专项抽查.已知该地区超市中卖的各种类型的奶粉的分布情况如下:老年人专用奶粉300种,普通奶粉240种,婴幼儿奶粉360种,现采用分层抽样的方法抽取150种进行检验,则这三种型号的奶粉依次应抽取( )
A.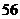 种,
种,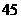 种,
种,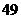 种 B.
种 B.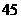 种,
种,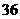 种,
种,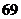 种
种
C.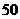 种,
种,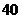 种,
种,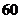 种
D.
种
D.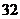 种,
种,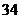 种,
种,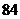 种
种
4.有下列命题:①已知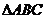 ,若
,若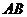 ∥平面
∥平面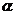 ,
,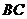 ∥平面
∥平面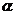 ,则
,则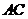 ∥平面
∥平面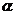 .
.
②已知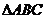 和直线
和直线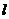 ,若
,若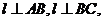 则
则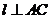 .③已知直线
.③已知直线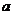 和平面
和平面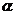 ,
,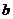 是平面
是平面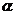 内任意一条直线,若
内任意一条直线,若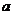 ∥
∥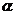 ,则
,则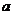 ∥
∥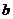 .④已知直线
.④已知直线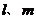 和平面
和平面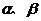 ,若
,若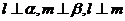 ,则
,则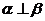 . 其中真命题的个数为( )
. 其中真命题的个数为( )
A.1
B.
5.用与球心距离为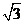 的平面去截球,所得截面面积为
的平面去截球,所得截面面积为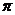 ,则截面直径的两个端点的球面距离为( )
,则截面直径的两个端点的球面距离为( )
A.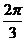 B.
B.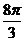 C.
C.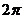 D.
D. 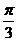
6.过抛物线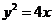 的焦点作一条直线与抛物线相交于
的焦点作一条直线与抛物线相交于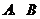 两点,它们的横坐标之和为
两点,它们的横坐标之和为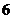 ,则这样的直线( )
,则这样的直线( )
A.有且仅有一条 B.有且仅有两条 C.有无穷多条 D.不存在
7.函数 的定义域为(
)
的定义域为(
)
A.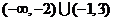 B.
B.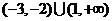
C.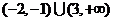 D.
D.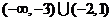
8.一次演讲比赛中,需要安排 名选手的出场顺序,方法是按照姓氏笔画的多少(由少到多)安排,如姓氏笔画数相同,则顺序任意.统计发现,10名选手中姓氏笔画为4画的有2人,5画的有3人,6画的有4人,7画的有1人,则不同的出场顺序共有( )
名选手的出场顺序,方法是按照姓氏笔画的多少(由少到多)安排,如姓氏笔画数相同,则顺序任意.统计发现,10名选手中姓氏笔画为4画的有2人,5画的有3人,6画的有4人,7画的有1人,则不同的出场顺序共有( )
A.24种 B.48种 C.144种 D.288种
9.定义在R上的函数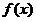 为奇函数,且
为奇函数,且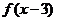 为偶函数.记
为偶函数.记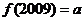 ,若
,若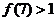 ,则一定有( )
,则一定有( )
A. 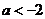 B.
B. 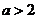 C.
C. 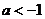 D.
D. 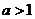
10.函数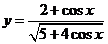 的值域是( )
的值域是( )
A.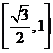 B.
B.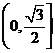 C.
C.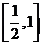 D.
D. 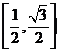
第 Ⅱ 卷(非选择题 共100分)
二、填空题:(本大题共5小题,每小题5分,共25分)
11.设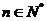 ,若
,若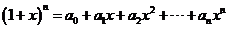 ,且
,且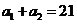 ,则在
,则在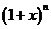 的展开式的各项系数中,最大系数的值是_______________.
的展开式的各项系数中,最大系数的值是_______________.
12.设双曲线 的两条渐近线与左准线围成的三角形区域(包含边界)为
的两条渐近线与左准线围成的三角形区域(包含边界)为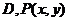 为
为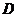 内的一个动点,则目标函数
内的一个动点,则目标函数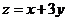 的最大值为______.
的最大值为______.
13.用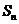 表示等差数列
表示等差数列 的前
的前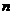 项和.若
项和.若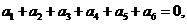
 ,
,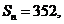 则此等差数列的项数
则此等差数列的项数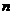 =_____.
=_____.
14.在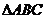 中,
中,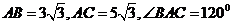 ,其所在平面外一点
,其所在平面外一点 到
到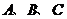 三个顶点的距离都是25,则
三个顶点的距离都是25,则 点到平面
点到平面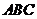 的距离为__________.
的距离为__________.
15.已知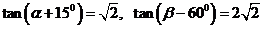 ,则
,则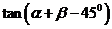 的值为 ,
的值为 ,
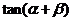 的值为
.
的值为
.
三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.)
16.(本题12分)已知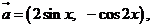
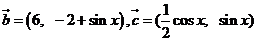 .其中
.其中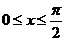 .
.
(1)若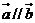 ,求
,求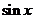 的值;
的值;
(2)设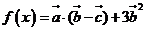 ,求
,求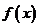 的最大值.
的最大值.
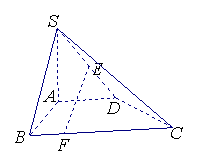 17.(本题12分)如图,在四棱锥
17.(本题12分)如图,在四棱锥 中,
中,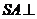 底面
底面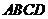 ,
,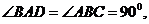
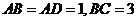 ,
,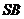 与平面
与平面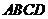 所成的角为
所成的角为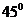 ,
, 为
为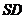 的中点.
的中点.
(1)若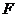 为线段
为线段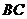 上的一点且
上的一点且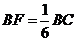 ,
,
求证: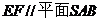 ;
;
(2)求点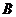 到平面
到平面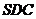 的距离;
的距离;
(3)在线段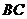 上是否存在一点
上是否存在一点 ,使二面角
,使二面角
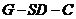 的大小为
的大小为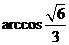 ?若存在,求出
?若存在,求出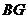 的长;若不存在,说明理由.
的长;若不存在,说明理由.
18.(本题12分)已知函数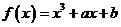 在点
在点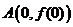 处的切线方程为
处的切线方程为 .
.
(1)求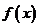 的单调区间;
的单调区间;
(2)若不等式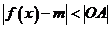 (O为原点)在
(O为原点)在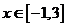 上恒成立,求实数的
上恒成立,求实数的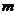 的取值范围.
的取值范围.
19.(本题12分)有一种游戏,要求游戏者从一个不透明的箱子中摸球,箱子中装有6个不同编号的白球和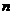 个
个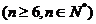 不同编号的黄球(这些球外形相同),操作一次就是从中摸出两球,若摸出的两球颜色不同,该次操作得
不同编号的黄球(这些球外形相同),操作一次就是从中摸出两球,若摸出的两球颜色不同,该次操作得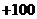 分;若摸出的两球颜色相同,该次操作得
分;若摸出的两球颜色相同,该次操作得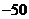 分.一个人操作若干次,如果总得分恰为
分.一个人操作若干次,如果总得分恰为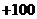 分,就称游戏“获胜”.
分,就称游戏“获胜”.
(1)若游戏参与者只有一次操作的机会,他“获胜”的概率为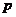 .试用
.试用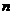 表示
表示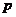 ,并求
,并求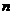 为何值时,
为何值时,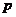 最大?
最大?
(2)若某个人连续操作四次(每次操作后把球放回),问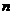 为何值时,他“获胜”的概率最大?
为何值时,他“获胜”的概率最大?
20.(本题13分)已知椭圆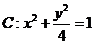 ,过点
,过点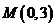 的直线
的直线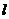 与椭圆
与椭圆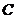 相交于不同的两点
相交于不同的两点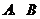 .
.
(1)若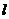 与
与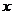 轴交于点
轴交于点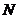 ,且
,且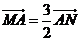 ,求直线
,求直线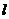 的方程;
的方程;
(2)设 为椭圆上一点,且
为椭圆上一点,且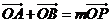 (O为原点),
(O为原点),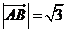 ,求实数
,求实数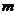 的值.
的值.
21.(本题14分)已知数列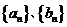 对任意正整数
对任意正整数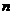 ,都有
,都有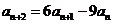 ,
,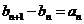 ,且
,且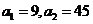 ,
,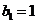 .
.
(1)求证:存在实数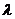 ,使数列
,使数列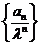 是等差数列;
是等差数列;
(2)求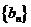 的通项公式;
的通项公式;
(3)求证:当 时,
时,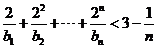 .
.
绝密★启用前(命题人:荣培元 审题人:杨少平)
2009年普通高等学校招生全国统一考试(荆中模拟卷)
第 Ⅰ 卷(共50分)
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案
B
B
C
C
A
B
D
D
C
A
二、填空题:
11. 20 12. 4 13. 22 14. 24 15. 
三、解答题:
16.解:(1)由 得
得
 ………………………………………2分
………………………………………2分




 …………………………6分
…………………………6分
(2)




 …………………………10分
…………………………10分



 ……………12分
……………12分
 17.解:(1)取SA的中点H,连结EH,BH
17.解:(1)取SA的中点H,连结EH,BH
 E是SD的中点
E是SD的中点




 四边形EFBH为平行四边形
四边形EFBH为平行四边形
 又
又
 ………………………4分
………………………4分
(2)


以 为原点,
为原点, 为
为 轴,
轴, 为
为 轴,
轴, 为
为 轴,如图所示建立直角坐标系,
轴,如图所示建立直角坐标系,
则

设 是平面
是平面 的法向量,则
的法向量,则


 取
取
则 到平面
到平面 的距离为
的距离为 …………………………8分
…………………………8分
(3)设 ,则
,则


设 是平面
是平面 的法向量,则
的法向量,则

 取
取
由 得
得
 , 故存在G点满足要求,
, 故存在G点满足要求, .
…………………………12分
.
…………………………12分
18.解:


由已知,得
 …………………………3分
…………………………3分
(1)
由 ,得
,得 或
或
由 ,得
,得
 的递增区间是
的递增区间是 ,递减区间是
,递减区间是 ……………………6分
……………………6分
(2)不等式即 


由 ,得
,得
又


 在
在 内最大值为6,最小值为-14
内最大值为6,最小值为-14


 的取值范围为
的取值范围为 …………………………12分
…………………………12分
19.解:(1) …………………………2分
…………………………2分


 随
随 的增大而增大
的增大而增大
 当
当 时,
时, …………………………6分
…………………………6分
(2)连续操作四次“获胜”的概率记作 ,则
,则



当且仅当  即
即 时取“=”
时取“=”
由 ,得
,得


 当
当 时,“获胜”的概率最大.
…………………………12分
时,“获胜”的概率最大.
…………………………12分
20.解:设A、B的坐标分别为
 的方程为:
的方程为:
(1)N点坐标





所求 的方程为:
的方程为: …………………………6分
…………………………6分
(2)由 得
得 

 ,
, ,
, 



设 点坐标为
点坐标为 , 显然
, 显然 




 …………………………13分
…………………………13分
21.解:(1)欲使 为等差数列,只需
为等差数列,只需
即 
令 得
得 
 存在实数
存在实数 ,使
,使 是等差数列.
…………………………3分
是等差数列.
…………………………3分
(2)

 是等差数列,
是等差数列,


 …………………………5分
…………………………5分




故 …………………………8分
…………………………8分
(3)当 时,
时,
又 ,
,


 左式
左式 .
…………………………14分
.
…………………………14分