2009-2010学年度山东省泗水县第一学期八年级期中考试
数学试题
(时间:120分钟)
同学们,你们好!一转眼半个学期飞快地过去了,在这半个学期里,我们又学到了许多新的数学知识,也提高了我们的数学思维能力,现在让我们在这里展示一下自己的真实水平吧!祝大家成功!
一、细心选一选,慧眼识金!(下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在下面的答题栏内)注意可以用各种不同的方法来解决你面前的选择题哦!
1.下列图案是轴对称图形的有( )

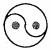


A.1个 B.2个 C.3个 D.4个
B.2个 C.3个 D.4个
2.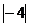 的平方根是(
)
的平方根是(
)
A.2 B.-2 C.±2 D.±4
3.下列说法中,错误的是( )
①只有两个三角形才能完全重合;
②如果两个图形是全等形,那么它们的形状和大小一定都相同;
③两个正方形一定是全等形;
④边数相同的图形一定能互相重合
A.①③④ B.①②③ C.①③ D.①④
4.点P(-2,1)关于x轴的对称点的坐标为( )
A.(2,1) B.(-2,-1) C.(2,-1) D.(1,-2)
5.等腰三角形一个外角等于110°,则底角的度数为( )
A.70°或40° B.40°或55° C.55°或70° D.70°
6.在实数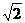 ,0,
,0, ,
,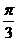 ,
,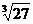 ,0.101001000 1……(每两个1之间依次多1个0)中,无理数的个数是( )
,0.101001000 1……(每两个1之间依次多1个0)中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
7.在下列式子中,正确的是( )
A.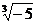 =-
=-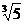 B.-
B.- =-0.6
=-0.6
C.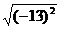 =-13 D.
=-13 D.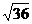 =±6
=±6
8.如下图所示,△ABC≌△EDF,DF=BC,AB=ED,AE=20,FC=10,则AC的长为( )
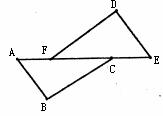
A.20 B.15 C.10 D.5
9.如下图所示,在Rt△ABC中,∠C=
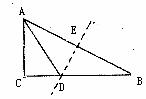
A.AC=AE=BE B.AD=BD C.AC=BD D.CD=DE
10.已知两条互不平行的线段AB、A’B’关于直线i对称,AB、A’B’所在的直线交于点P,下面四个结论中错误的是( )
A.AB=A’B’ 
B.点P不在直线i上
C.若点A、A’是对称点,则直线i垂直平分线段AA’
D.若点B、B’是对称点,则PB=PB’
11.如下图所示,光线L照射到平面镜I上,然后在平面镜I、Ⅱ之间来回反射,如果∠α=55°,∠γ=75°,则∠β为( )
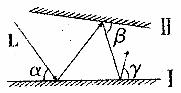
A.50° B.55° C.60° D. 65°
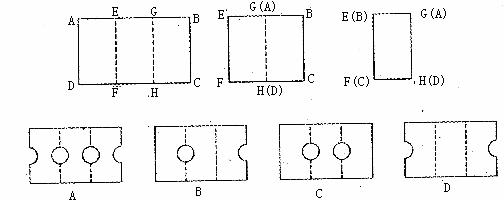
12.如下图所示,将矩形纸片ABCD沿虚线EF折叠,使点A落在点G上,点D落在点H上;然后再沿虚线GH折叠,使B落在点E上,点C落在点F上;叠完后,剪一个直径在BC上的半圆,再展开,则展开后的图形为( )
二、开动脑筋,耐心填一填!
13.要使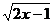 有意义,则x的取值范围是________
有意义,则x的取值范围是________
14.在平面直角坐标系中,点A关于y轴对称的点A’的坐标为(-2,7),则点A的坐标为_______
15.如下图所示,在等边△ABC中,AD⊥BC,BD=3,则∠1的度数为 ______,AB= ______
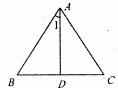
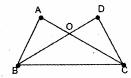
16.如下图所示,∠ACB=∠DBC,要想说明△ABC≌△DCB,只需增加的一个条件是______(只需填一个你认为合适的条件).
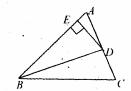
17.如下图所示,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=
18.观察下列各式: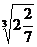 =2
=2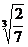 ,
, 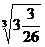 =3
=3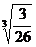 ,
,  =4
=4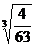 ,
, 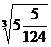 =5
=5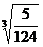 ……将你发现的规律用含n的式子表示为____(n为大于1的正整数)
……将你发现的规律用含n的式子表示为____(n为大于1的正整数)
如果你觉得有的题目有点困难,那么把解答写出一部分也可以,可不要有题目下面是空白 的喔!
三、耐心做一做,你一定是学习中的强者(解答要求写出必要的计算步骤或证明过程)
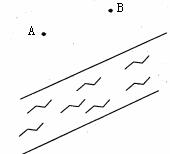
19.如下图所示,A、B两村在一条小河的的同一侧,现要在河边建一水厂M向两村供水,若要使自来水厂M到两村的距离和最短,厂址应选在哪个位置最合适? (并保留作图痕迹)
20.计算
(1)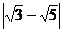 +
+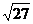 -
-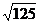 (2)-12+
(2)-12+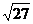 ×
×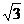 -2
-2
21.如下图所示,由小正方形组成的L形图中,请你用三种方法分别在下图中再添画一个小正方形使它成为轴对称图形:
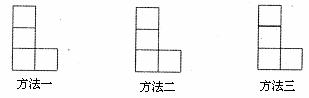
22.如下图所示,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线,为什么?
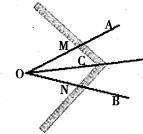
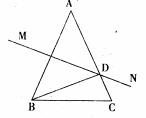
23.如下图所示,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,求∠DBC的度数?
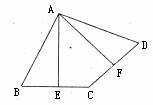
24.如下图所示,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD
(1)求证:AB=AD
(2)请你探究∠EAF、∠BAE、∠DAF之间存在怎样的数量关系?并证明你的结论。
25.问题背景:
在△ABC中,AB、BC、AC三边的长分别为 、
、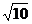 、
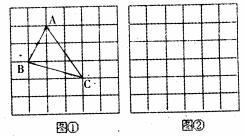
、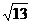 ,求这个三角形的面积。小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点(即三个顶点都在小正方形的顶点处),如图①所示,这样不需求△ABC的高,而借用网格就能计算出它的面积。
,求这个三角形的面积。小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点(即三个顶点都在小正方形的顶点处),如图①所示,这样不需求△ABC的高,而借用网格就能计算出它的面积。
(1)请你将△ABC的面积直接填写在横线上。
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法。若△ABC三边的长分别为 a、
a、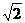 a
a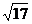 a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积。
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积。
探索创新:
(3)若△ABC三边的长分别为、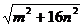 、
、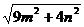 、
、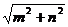 m
m
请再仔细检查一下,也许你会做的更好,考试成功的秘诀在于把会做的题做对,祝你成功!