2009-2010学年度滨州市阳信第一学期八年级期中学业水平检测
数学试卷
一、选择(每题4分共40分)
1.国旗是一个国家的象征,观察下面的国旗,是轴对称图形的是( )

A.加拿大、哥斯达黎加、乌拉圭 B.加拿大、瑞典、澳大利亚
B.加拿大、瑞典、澳大利亚
C.加拿大、瑞典、瑞士 D.乌拉圭、瑞典、瑞士
2.在直角坐标系中,A(1,2)点的横坐标乘以-1,纵坐标不变,得到点,则A它与的关系是( )
A.关于 轴对称
B.关于
轴对称
B.关于 轴对称 C.关于原点轴对称 D.不确定
轴对称 C.关于原点轴对称 D.不确定
3.已知△ABC在直角坐标系中的位置如图所示,如果△A’B’C’与△ABC关于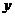 轴对称,那么点A的对应点A’的坐标为( ).
轴对称,那么点A的对应点A’的坐标为( ).
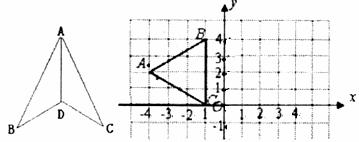
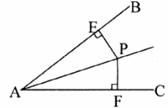
A.(-4,2) B.(-4,-2) C.(4,-2) D.(4,2)
4.如图,AB=AC,BD=CD可根据( )得到△ABD≌△ACD
A.SAS B.ASA C.SSS D.HL
5.若实数m满足m-|m|=0,则m的取值范围是( ).
A.m≥0 B.m>
6.如图是跷跷板的示意图,支柱OC与地面垂直,点O是横板AB的中点,AB可以绕着O上下转动,当A端落地时,∠OAC=20°,横板上下可转动的最大角度(即∠A’OA)是( ).

A.80° B.60° C.40° D.20°
7.如图所示,AD∥BC,AC=BD,AB=CD,图中全等的三角形的对数是( )
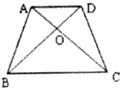
A.2 B.
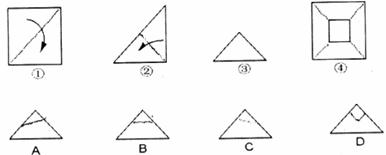
8.将一张纸片沿图中①、②的虚线对折得图中的③,然后剪去一个角,展开铺平后的图形如图中的④,则图中的③沿虚线的剪法是( )
9.下列命题正确的是( )
A.负数没有立方根
B.-7的立方根是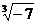
C. =2
=2
D.任何正数都有两个立方根,它们互为相反数
10.在△ABC和△A’B’C’中有①AB=A’B’②BC=B’C’③AC=A’C’④∠A=∠A’,⑤∠B=∠B’⑥∠C=∠C’,则下列各组条件中不能保证△ABC≌△A’B’C’的是( )
A.①②③ B.①②⑤ C.①②④ D.②⑤⑥
B.①②⑤ C.①②④ D.②⑤⑥
二.填空:(每题3分,共30分)
11.已知实数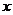 、
、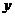 满足
满足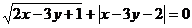 ,则
,则
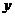 的平方根是__________.
的平方根是__________.
12.如图,A,B,C,D在同一直线上,AB=CD,DE∥AF,若要使△ACF≌△DBE,则还需要补充一个条件:__________或__________.
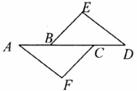
13.如图中有6个条形方格图,图上由实线围成的图形是全等形的有__________.
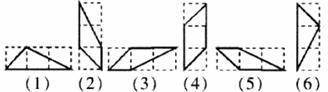
14.如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=
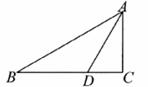
15.如图,点P是∠BAC的平分线上一点,PE⊥AB,PF⊥AC,E、F分别为垂足,①PE=PF②AE=AF③∠APE=∠APF,上述结论中正确的是__________ (只填序号)。
16.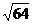 的立方根是__________
的立方根是__________
17.在平面直角坐标系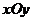 中,已知点A(2,-2),在
中,已知点A(2,-2),在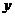 轴上确定点P,使△AOP为等腰三角形,则符合条件的有__________个.
轴上确定点P,使△AOP为等腰三角形,则符合条件的有__________个.
18.在 …中,无理数有__________个.
…中,无理数有__________个.
19.若P关于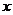 轴的对称点为(3,a),关于
轴的对称点为(3,a),关于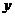 轴对称的点为(b,2),则P点的坐标为_________。
轴对称的点为(b,2),则P点的坐标为_________。
20.如图所示,有一块三角形田地,AB=AC=
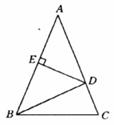
三、简答(共6题,共60分)
21.化简(每题5分,共10分)
(1)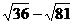 (2)
(2)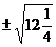
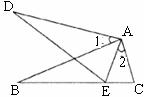
22.(10分)如图,已知AB=AD,AC=AE,∠1=∠2,求证:△ABC≌△ADE
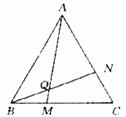
23.(10分)△ABC为正三角形,点M是射线BC上任意一点,点N是射线CA上任意一点,且BM=CN,BN与AM相交于Q点,∠AQN等于多少度.
24.(10分)如图甲,正方形被划分成16个全等的三角形,将其中若干个三角形涂黑,且满足下列条件:
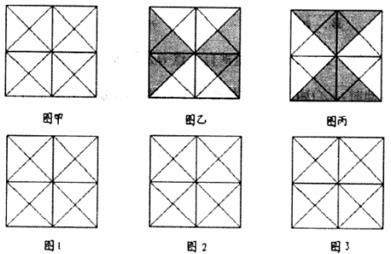
(1)涂黑部分的面积是原正方形面积的一半;
(2)涂黑部分成轴对称图形.
图乙与图丙是一种涂法,请在图1~3中分别设计另外三种涂法.(注:在所设计的图案中,若涂黑部分全等,则认为是同一种涂法,如图乙与图丙)
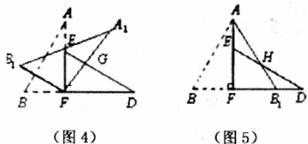
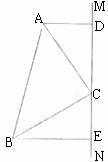
25.(10分)△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN,BE⊥MN于E,求证:DE=AD+BE
26.(10分)如图1,小明将一张矩形纸片沿对角线剪开,得到两张全等直角三角形纸片(如图2),量得他们的斜边长为
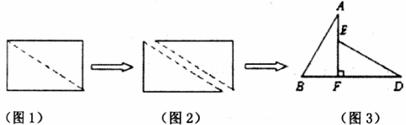
小明在对这两张三角形纸片进行如下操作时遇到了两个问题,请你帮助解决。
(1)将图3中的△ABF绕点F顺时针方向旋转30°到图4的位置,A
(2)将图3中的△ABF沿直线AF翻折到图5的位置,AB1交DE于点H,请证明:AH=DH.