2009-2010学年度辽宁省大石桥市第一学期九年级期中考试
数学试卷
一、选择题(每小题3分,共30分)
1.用配方法解方程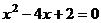 ,下列配方正确的是
,下列配方正确的是
A.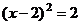
 B.
B.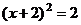
C.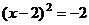 D.
D.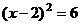
2.从早上太阳升起的某一时刻开始到晚上,旭日广场的旗杆在地面上的影子的变化规律是
A.先变长,后变短 B.先变短,后变长
C.方同改变,长短不变 D.以上都是不正确
3.在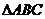 中,
中,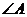 ,
,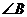 ,
,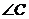 的对边分别是
的对边分别是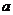 ,
,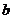 ,
,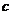 且
且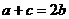 ,
,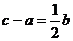 则
则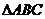 是
是
A.直角三角形 B.等边三角形
C.等腰三角形 D.等腰直角三角形
4.等边三角形一边上高长为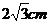 ,那么这个等边三角形的中位线长为
,那么这个等边三角形的中位线长为
A.
5.一个等腰梯形的两底之差为12,高为6,则等腰梯形的锐角为
A.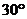 B.
B.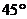 C.
C.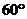 D.
D.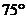
6.一个圆柱体钢块,正中央被挖去了一个长方体孔,其俯视图如图所示,则此圆柱体钢块的左视图是
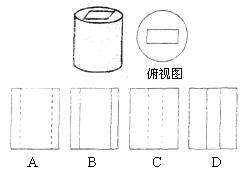
7.若 ,
,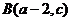 两点均在函数
两点均在函数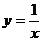 的图象上,且
的图象上,且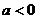 ,则
,则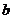 与
与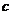 的大小关系为
的大小关系为
A.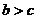 B.
B.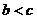 C.
C.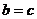 D.无法判断
D.无法判断
8.已知反比例函数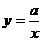
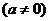 的图象,在每一象限内,
的图象,在每一象限内,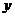 的值随
的值随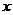 值的增大而减少,则一次函数
值的增大而减少,则一次函数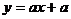 的图象不经过
的图象不经过
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.函数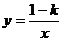 的图象与直线
的图象与直线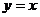 没有交点,那么
没有交点,那么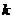 的取值范围是
的取值范围是
A.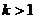 B.
B. C.
C. D.
D.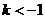
10.已知三角形的面积一定,则它底边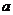 上的高
上的高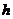 与底边
与底边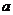 之间的函数关系的图象大致是
之间的函数关系的图象大致是
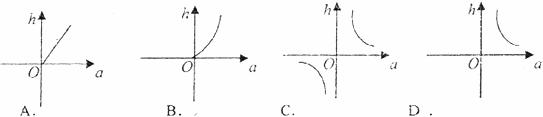
二、填空题(每小题3分,共24分)
11.将方程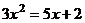 化为一元二次方程的一般形式为________________________;
化为一元二次方程的一般形式为________________________;
12.若关于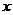 的一元二次方程
的一元二次方程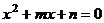 有两个实数根,则符合条件的一组
有两个实数根,则符合条件的一组 、
、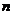 的实数值可以是
的实数值可以是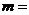 _________________,
_________________,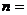 _______________。
_______________。
13.平行四边形ABCD中,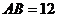 ,AB边上的高为3,BC边上的高为6,则平行四边形ABCD的周长为__________________。
,AB边上的高为3,BC边上的高为6,则平行四边形ABCD的周长为__________________。
14.已知直线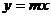 与双曲线
与双曲线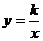 的一个交点A的坐标
的一个交点A的坐标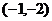 ,则
,则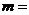 _________,
_________,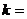 ______;它们的另一个交点坐标是________________。
______;它们的另一个交点坐标是________________。
15.为了美化环境,某市加大对绿化的投资,2007年用于绿化投资20万元,2009年用于绿化投资25万元,求这两年绿化投资的年平均增长率,设这两年绿化投资的年平均增长率为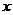 ,根据题意所列方程为_____________________。
,根据题意所列方程为_____________________。
16.“对应角相等的三角形是全等三角形”的逆命题是___________________________,它是__________(填“真”或“假”)命题。
17.将一个三角板放在太阳光下,它所形成的投影是_____________,也可能是_______________。
18.小明有道数学题不会,想打电话请教老师,可是他只想起了电话号码的前6位(共7位数的电话),那么他一次打通电话的概率是____________。
三、解答题
19.(12分)解下列方程
(1)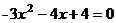
(2)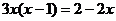
20.(10分)如图,已知一次函数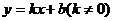 的图象与
的图象与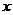 轴、
轴、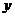 轴分别交于A、B点,且与反比例函数
轴分别交于A、B点,且与反比例函数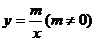 的图象在第一象限交于点C,CD垂直于
的图象在第一象限交于点C,CD垂直于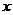 轴,垂足为D。若
轴,垂足为D。若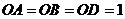 。
。
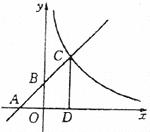
(1)求点A、B、D的坐标。
(2)一次函数和反比例函数的解析式。
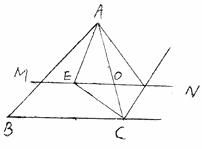
21.(12分)在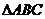 中,点O是边AC上的一个对动点,过点O作直线MN∥BC,设MN交
中,点O是边AC上的一个对动点,过点O作直线MN∥BC,设MN交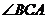 的平分线于点E,交
的平分线于点E,交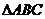 的外角
的外角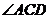 的平分线于点F。
的平分线于点F。
(1)求证:OE=OF。
(2)当点O运动到何处时,四边形AECF是矩形?证明你的结论。
四、实际应用题
22.(8分)今秋以来,在党和政府的领导下,我国进行了一场抗击“H1N
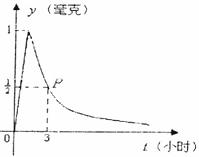
23.(10分)为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒。已知药物释放过程中,室内每立方米空气中的含药盒量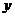 (毫克)与时间
(毫克)与时间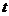 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,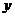 与
与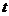 的函数关系式为
的函数关系式为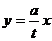 (
(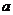 为常数),如图所示,据图中提供的信息,解答下列问题:
为常数),如图所示,据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,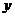 与
与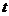 之间的两个函数关系式及相应的自变量的取值范围;
之间的两个函数关系式及相应的自变量的取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
五、创新多变
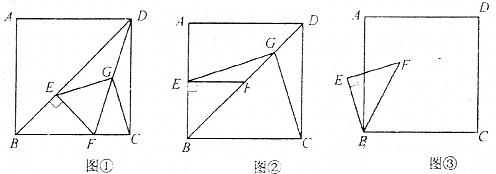
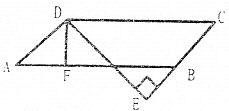
24.(10分)已知正方形ABCD中,E为对角线BD上一点,过E点作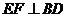 交BD于F,连接DF,G为DF中点,连接EG,CG。
交BD于F,连接DF,G为DF中点,连接EG,CG。
(1)求证:EG=CG;
(2)将图①中的 绕B点逆时针旋转
绕B点逆时针旋转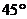 ,如图②所示,取DF中点G,连接EG,CG。问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由。
,如图②所示,取DF中点G,连接EG,CG。问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由。
(3)将图①中的 绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)