2008-2009学年度北京市西城区第二学期七年级期末测试
数学试卷
一、精心选一选(共10个小题,每小题3分,共30分)
1.下列四个算式中,正确的个数有( ).
①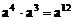 ②
②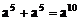 ③
③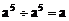 ④
④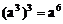
A.0个 B.1个 C.2个 D.3个
2.在数轴上表示不等式组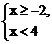 的解集,正确的是( ).
的解集,正确的是( ).

3.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( ).
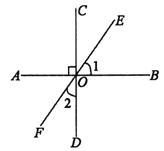
A.相等 B.互余 C.互补 D.互为对顶角
4.已知一个样本:23,24,25,26,26,27,27,27,27,27,28,28,28,29,29,30,30,31,31,32,那么频数为8的范围是( ).
A.24.5~26.5 B.26.5~
5.化简: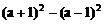 =( ).
=( ).
A.2 B.
6.下列命题中是假命题的是( ).
A.同旁内角互补,两直线平行
B.直线a⊥b,则a与b的夹角为直角
C.如果两个角互补,那么这两个角一个是锐角,一个是钝角
D.若a∥b,a⊥c,那么b⊥c
7.下列变形中不正确的是( ).
A.由a>b得b<a B.由-a>-b得b>a
C.由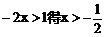 D.由
D.由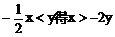
8.下列变形是因式分解的是( ).
A.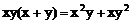 B.
B.
C.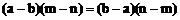 D.
D.
9.科技馆为某机器人编制一段程序,如果机器人在平地上按照下图中的步骤行走,那么该机器人所走的总路程为 ( )。

A.
10.已知△ABC中,三边长a,b,c都是正整数,且满足a>b>c,a=8,那么满足条件的三角形共有( )个.
A.6 B.
二、细心填一填(共10个小题,每小题2分,共20分)
11.因式分解: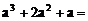 .
.
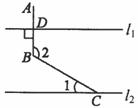
12.如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=30°,则∠2= .
13.若点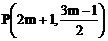 在第四象限,则m的取值范围是
.
在第四象限,则m的取值范围是
.
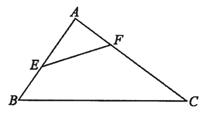
14.如图,一个顶角∠A为90°的直角三角形纸片,剪去这个角后得到一个四边形,则∠BEF+∠CFE的度数是 度.
15.用“※”定义新运算:对于任意有理数a、b,都有a※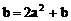 . 例如3※
. 例如3※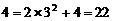 ,那么
,那么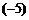 ※2=
;当m为有理数时,m※(m※2)= .
※2=
;当m为有理数时,m※(m※2)= .
16.已知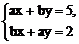 的解是
的解是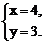 则a=
,b= .
则a=
,b= .
17.如果一个多边形的内角和等于它的外角和的3倍,那么这个多边形是 边形.
18.如果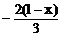 的值是非正数,那么x的取值范围是
.
的值是非正数,那么x的取值范围是
.
19.如图,△ABC中,∠ABC=∠BAC,∠BAC的外角平分线交BC的延长线于点D,∠ADC=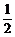 ∠CAD,则∠ABC等于 度.
∠CAD,则∠ABC等于 度.
20.生活中,有人喜欢把传送的便条折成 形状,折叠过程是这样的(阴影部分表示纸条的反面):
形状,折叠过程是这样的(阴影部分表示纸条的反面):
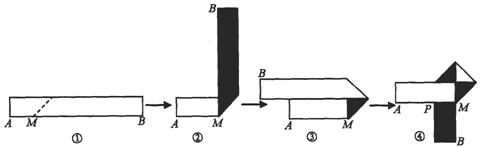
如果由信纸折成的长方形纸条(图①)长为
三、认真做一做(每小题5分,共30分)
21.先化简,再求值:
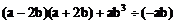 ,其中
,其中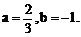
22.解方程组: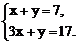
23.解不等式组: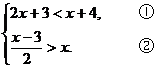
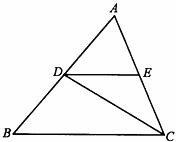
24.如图,CD平分∠ACB,DE∥BC,∠AED=80°
(1)求∠EDC;
(2)若BC=10,S△BCD=30,求点E到BC的距离.
25.在平面直角坐标系中有四个点,它们的坐标分别是A(0,3),B(-2,-1),C(3,-1),D(5,3).
(1)在坐标系中描出这四个点,并依次连接它们,画出所得图形;
(2)将所得的图形向下平移2个单位长度,画出平移后的图形,写出平移后对应的四点A',B',C',D'的坐标.

26.A,B,C三名大学生竞选学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表一和图一:
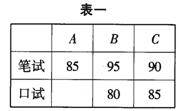
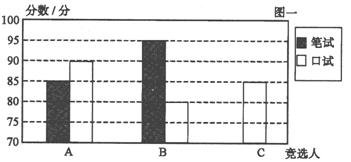
(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.

六、解答题(每小题5分,本题共20分)
27.为改善办学条件,东海中学计划购买部分A品牌电脑和B品牌课桌.第一次,用9万元购买了A品牌电脑10台和B品牌课桌200张.第二次,用9万元购买了A品牌电脑12台和B品牌课桌120张.
(1)每台A品牌电脑与每张B品牌课桌的价格各是多少元?
(2)第三次购买时,销售商对一次购买量大的客户打折销售.规定:一次购买A品牌电脑35台以上(含35台),按九折销售,一次购买B品牌课桌600张以上(含600张),按八折销售。学校准备用27万元购买电脑和课桌,其中电脑不少于35台,课桌不少于600张,问有几种购买方案?
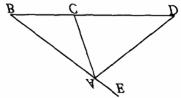
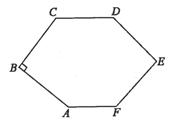
28.如图。CD//AF,∠CDE=∠BAF,AB⊥BC,∠C=128°,∠E=80°,求∠F的度数。
29.如果有理数x,y满足等式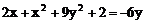 ,求
,求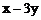 的值。
的值。
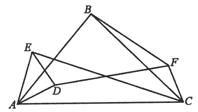
30.如图,△ADE和△ABC中∠EAD=∠AED=∠BAC=∠BCA=45°,又有∠BAD=∠BCF.
(1)求∠ECF+DAC+∠ECA的度数;
(2)判断ED与FC的位置关系,并对你的结论加以证明.