2008-2009学年度滕州市奎文北区九年级质量监测
数学试卷
说明:本试题满分120分,考试时间120分钟。
第Ⅰ卷(选择题 共36分)
一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分。选错、不选或选出的答案超过一个均记零分。)
1.下列算式中,正确的是
A.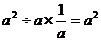 B.
B.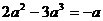
C.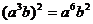 D.
D.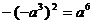
2.下面是一位美术爱好者利用网格图设计的几个英文字母的图形,你认为其中既是轴对称图形又是中心对称图形的是
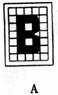

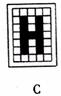

3.在下列命题中,正确的是
A.一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.有一组邻边相等的平行四边形是菱形
D.对角线互相垂直平分的四边形是正方形
4.如下图,从点P向⊙O引两条切线PA,PB,切点为A,B,BC为⊙O的直径,若∠P=60°,PA=3,则⊙O的直径BC的长为
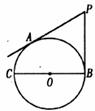
A.3 B.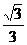 C.
C.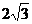 D.
D.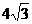
5.已知⊙O1的半径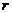 为
为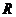 为
为
A.相交 B.内含 C.内切 D.外切
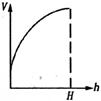
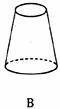
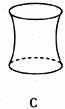
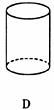
6.向高为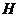 的水瓶中注水,注满为止,如果注水量
的水瓶中注水,注满为止,如果注水量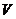 与水深
与水深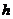 的函数关系的图像如下左图所示,那么水瓶的形状是
的函数关系的图像如下左图所示,那么水瓶的形状是

7.如下图,点A、B、C、D、E、F、G、H、K都是7×8方格纸中的格点,为了使△DEM∽△ABC,则点M应是F、G、H、K四点中的
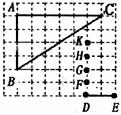
A.H B.G C.F D.K
8.下列图形中阴影部分的面积相等的是

A.①② B.②③ C.①④ D.③④
9.如下左图,是某一立方体的侧面展开图,则该立方体是


10.为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如下图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是
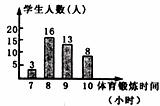
A.8,9 B.8,
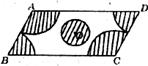
11.北京市一居民小区为了迎接2008年奥运会,计划将小区内的一块平行四边形ABCD场地进行绿化,如下图阴影部分为绿化地,以A、B、C、D为圆心且半径均为3m的四个扇形的半径等于图中⊙O的直径,已测得AB=6m,则绿化地的面积为( ) 。
。
A.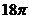 B.
B. C.
C.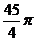 D.
D.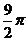
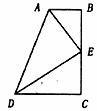
12.如图,在梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=4,E为BC中点,AE平分∠BAD,连接DE,则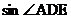 的值为
的值为
A.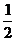 B.
B.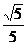 C.
C. D.
D.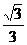
第Ⅱ卷(非选择题 共84分)
二、填空题(本大题共6小题,共24分,只要求填写最后结果,每小题填对得4分)
13.若式子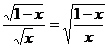 成立,则
成立,则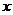 满足的条件为__________。
满足的条件为__________。
14.某超市在节日期间开展优惠活动,凡一次性消费不超过200元的一律九折优惠,超过200元的,其中200元按九折算,超过200元的部分按八折算,王老师第一次购物付款72元,第二次又去购物享受了八折优惠,他查看了所买物品的发票,发现两次共节省了34元。则王老师第二次购物实际付款__________元。
15.2008年5月12日,四川汶川发生里氏8.0级地震,国内外社会各界纷纷向灾区捐款捐物,抗震救灾。截止6月4日12时,全国共接收捐款约为43681000000元人民币。这笔款额用科学记数法表示(保留三个有效数字)为__________元。
16.已知一个圆锥的底面半径为4,母线长为8,则该圆锥的侧面积为__________。
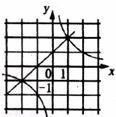
17.如下图,是一次函数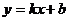 与反比例函数
与反比例函数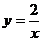 的图像,则关于
的图像,则关于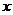 的方程
的方程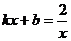 的解为__________。
的解为__________。
18.对于实数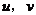 ,定义一种运算“
,定义一种运算“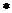 ”为:
”为: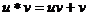 。若关于
。若关于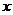 的方程
的方程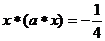 有两个相等的实数根,则满足条件的实数
有两个相等的实数根,则满足条件的实数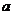 的值是__________。
的值是__________。
三、解答题(共7小题,满分60分,解答应写出文字说明、证明过程或演算步骤。)
19.(本题满分6分)
已知: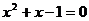 ,求代数式的值:
,求代数式的值: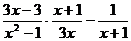
20.(本题满分6分)
水果种植大户小方,为了吸引更多的顾客,组织了观光采摘游活动。每一位来采摘水果的顾客都有一次抽奖机会:在一只不透明的盒子里有A、B、C、D四张外形完全相同的卡片,抽奖时先随机抽出一张卡片,再从盒子中剩下的3张中抽取第二张。
(1)请你利用树状图(或列表)的方法,表示前后两次抽得酌卡片所有可能的情况。
(2)如果抽得的两张卡片是同一种水果图片就可获得奖励,那么得到奖励的概率是多少?
21.(本题满分8分)
北京至滕州高速铁路工程指挥部,要对某路段工程进行招褥,接到了甲、乙两个工程队的投标书。从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的 ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成。
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成。
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元。工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加 预算多少万元?请给出你的判断并说明理由.
22.(本小题满分6分)
已知:如下图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E。

(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明。
23.(本题满分10分)
如下图,边长为2的等边三角形OBA的顶点A在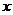 轴的正半轴上,B点位于第二象限。将△OAB绕点O顺时针旋转30°后,得到
轴的正半轴上,B点位于第二象限。将△OAB绕点O顺时针旋转30°后,得到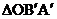 ,点
,点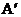 恰好落在双曲线
恰好落在双曲线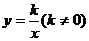 上。
上。
(1)在图中画出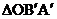 。
。
(2)求双曲线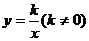 的解析式。
的解析式。
(3)等边三角形 绕着点O继续按顺时针方向旋转________度后,
绕着点O继续按顺时针方向旋转________度后, 点再次落在双曲线上?(直接将答案填写在横线上即可,不需要说明理由)
点再次落在双曲线上?(直接将答案填写在横线上即可,不需要说明理由)
24.(本题满分12分)
如下图,在平面直角坐标系中,A,B两点的坐标分别为A(-2,0),B(8,0),以AB为直径的半圆P与 轴交于点M,以AB为一边作正方形ABCD。
轴交于点M,以AB为一边作正方形ABCD。
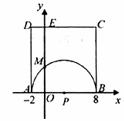
(1)求C,M两点的坐标。
(2)试判断直线CM与半圆P的位置关系,并证明你的结论。
(3)在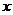 轴上是否存在一点Q,使得△QMC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由。
轴上是否存在一点Q,使得△QMC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由。
25.(本题满分12分)
如下图,设抛物线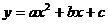 与
与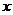 轴交于两个不同的点A(-1,0),B(
轴交于两个不同的点A(-1,0),B(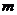 ,0),与
,0),与 轴交与点C(0,-2),且∠ACB=90°。
轴交与点C(0,-2),且∠ACB=90°。
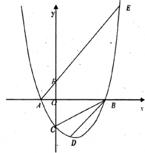
(1)求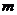 的值和抛物线的解析式。
的值和抛物线的解析式。
(2)已知点D(1, )在抛物线上,过点A的直线
)在抛物线上,过点A的直线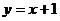 交抛物线于另一点E,求点D和点E的坐标。
交抛物线于另一点E,求点D和点E的坐标。
(3)在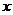 轴上是否存在点P,使以点P,B,D为顶点的三角形与三角形AEB相似,若存在,请求出点P的坐标,若不存在,请说明理由。
轴上是否存在点P,使以点P,B,D为顶点的三角形与三角形AEB相似,若存在,请求出点P的坐标,若不存在,请说明理由。