2008-2009学年度潍坊市高密第二学期八年级期末考试
数学试卷
共120分 考试时间120分钟
一、选择题(本大题共12题,在每题给出的四个选项中,只有一个是正确的。请把正确的选项选出来.每题选对得3分,选错、不选或选出的答案超过一个均记零分.)
1.使分式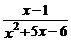 有意义的
有意义的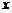 的取值范围是
的取值范围是
A.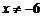 B.
B.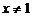 C.
C.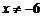 且
且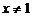 D.
D.
2.按下列条件画三角形,能唯一确定三角形形状和大小的是
A.三角形的一个内角为60°,一条边长为
B.三角形的两个内角为30°和70°
C.三角形的两条边长分别为
D.三角形的三条边长分别为
3.化简 的结果为
的结果为
A.1 B.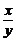 C.
C. D.
D.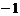
4.如果一组数据6,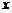 ,2,4的平均数为5,那么数
,2,4的平均数为5,那么数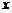 为
为
A.8 B.5. C.4 D.3
5.作△ABC的高AD、中线AE、角平分线AF,三者中有可能在△ABC的外部是
A.AD B.AE C.AF D.都有可能
6.点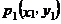 、
、 是一次函数
是一次函数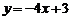 图象上的两个点,且
图象上的两个点,且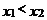 ,则
,则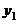 与
与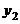 的大小关系是
的大小关系是
A.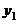 >
>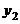 B.
B.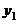 >
>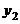 >
>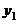 <
<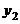 D.
D.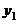 =
=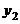
7.下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是

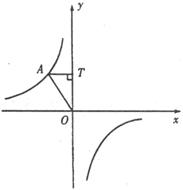
8.如图,点A是反比例函数图象上的一点,自点A向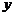 轴作垂线,垂足为T,已知△AOT的面积为4,则此函数的表达式为
轴作垂线,垂足为T,已知△AOT的面积为4,则此函数的表达式为
A.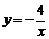 B.
B.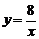 C.
C. D.
D.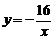
9.“龟兔赛跑”讲述了这样一个故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点…….用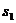 、
、 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程, 为时间,则下列图像中与故事情节吻合的是
为时间,则下列图像中与故事情节吻合的是
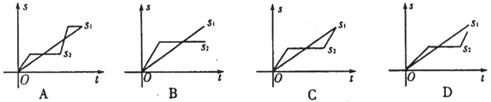
10.如图,直线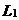 、
、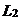 、
、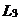 三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )处.
三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )处.
A.1 B.2 C.3 D.4
11.五个整数从小到大排列后,中位数为4,这组数据的惟一众数是6,那么这5个整数和的最大值可能是
A.21 B.22 C.23 D.24
12.如图,平行四边形ABCD中,E是AD的中点,连结OE,则△DOE的面积与平行四边形ABCD的面积之比是
A.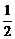 B.
B.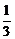 C.
C. D.
D.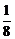
二、填空题(本大题共5题,共15分.只要求填写最后结果,每题填对得3分.)
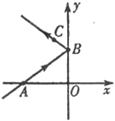
13.在平面直角坐标系中,入射光线经过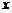 轴上点A(一3,0) ,由
轴上点A(一3,0) ,由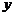 轴上点B反射,反射光线经过点C(一1,3),则B点的坐标是________.
轴上点B反射,反射光线经过点C(一1,3),则B点的坐标是________.
14.如图,在平行四边形ABCD中,E、F分别为AB、DC的中点,连结DE、EF、FB,则图中共有________个平行四边形.

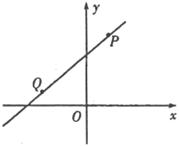
15.如图,一次函数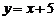 的图象经过点
的图象经过点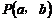 和
和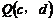 ,则
,则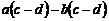 的值为________.
的值为________.
16.老师给出一个函数,甲、乙各指出了这个函数的一个性质:
甲:第一、三象限有它的图象;
乙:在每个象限内,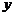 随
随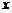 的增大而减小.
的增大而减小.
请你写一个满足上述性质的一个函数解析式________.
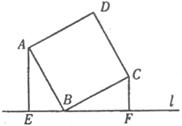
17.如图,直线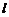 过正方形ABCD的顶点B,点A、C到直线
过正方形ABCD的顶点B,点A、C到直线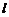 的距离分别是
的距离分别是 和
和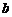 ,则正方形的边长是________.
,则正方形的边长是________.
三、解答题(本大题共7题,共69分.解答应写出文字说明、证明过程或推演步骤)
18.(本题满分8分)
一组学生租一辆汽车去旅游,租车费共需120,后来人数增加了 ,总租车费不变,这样每人少摊3元,原来这组学生的人数是多少?
,总租车费不变,这样每人少摊3元,原来这组学生的人数是多少?
19.(本题满分9分)
八年级一、二班举行投篮比赛,每班各挑选10名同学代表班级共参加5场投篮比赛,投篮得分如下:

1
2
3
4
5
一班
85
88
77
75
85
二班
95
85
70
80
80
(1)分别求出两个班五场比赛得分的平均值;
(2)你认为哪个班级的得分较稳定?为什么?
20.(本题满分9分)
如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
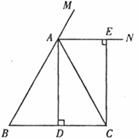
(1)求证:四边形ADCE为矩形;
(2)当四边形ADCE是一个正方形时,试判断△ABC的形状.
21.(本题满分10分)
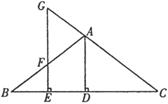
如图,△ABC中,AD⊥BC于D点,E为BD上的一点,EG∥AD,分别交AB和CA的延长线于F、G两点,∠AFG=∠AGF
(1)求证:△ABD≌△ACD.
(2)若∠ABC=40°,求∠GAF的大小.
22.(本题满分10分)
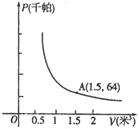
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气球体积V(米3)的反比例函数,其图象如图所示(千帕是一种压强单位).
(1)写出这个函数解析式;
(2)当气球的体积为0.8立方米时,气球内的气压是多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米?
23.(本题满分11分)
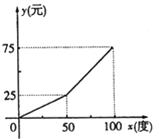
为了缓解用电紧张的矛盾,某电力公司特制定了新的用户用电收费标准,每月用电量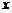 (度)与应付电费
(度)与应付电费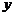 (元)的关系如图所示.
(元)的关系如图所示.
(1)根据图象,请分别求出当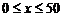 和
和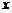 >50时,
>50时,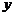 关于
关于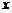 的函数关系式;
的函数关系式;
(2)请回答:
当每月用电量不超过50度时,收费标准是________________;
当每月的用电量越过50度时,收费标准是________________.
24.(本题满分12分)
如图所示,已知△ACM和△CBN都是等边三角形,点A、C、B在同一直线上,连接AN、MB.
(1)求证:AN=BM.
(2)若等边三角形CBN绕顶点C顺时针旋转后(旋转角 ),此时AN与BM是否还相等?若相等,给出证明;若不相等,说明理由.
),此时AN与BM是否还相等?若相等,给出证明;若不相等,说明理由.
