2009年阿坝州初中毕业暨高中阶段学校招生考试
数学试卷
(本试卷满分150分,考试时间l20分钟)
A卷(100分)
一、选择题(本大题共l0小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.计算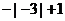 结果正确的是 ( )
结果正确的是 ( )
A.4 B.
2.下列运算正确的是 ( )
A.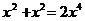 B.
B.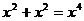 C.
C.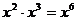 D.
D.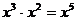
3.函数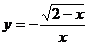 的自变量
的自变量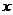 的取值范围是 ( )
的取值范围是 ( )
A.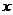 >2
B.
>2
B.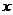 ≤2且
≤2且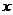 ≠0
≠0
C.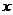 ≤2 D.
≤2 D.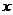 <2且
<2且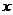 ≠0
≠0
4.三峡大坝是世界上最大的水利枢纽工程.据报道,三峡水电站年平均发电量为846.89亿度,用科学记数法记作(保留三位有效数字) ( )
A.8.47×1011度 B.8.46×1010度
C.8.47×109度 D.8.47×1010度
5.下列图案都是由字母“m”经过变形、组合而成的,其中不是中心对称图形的是( )

6.下列命题中,真命题是 ( )
A.两条对角线相等的四边形是矩形
B.两条对角线垂直的四边形是菱形
C.两条对角线垂直且相等的四边形是正方形
D.两条对角线相等的平行四边形是矩形
7.若关于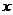 的一元二次方程
的一元二次方程 有实数根,则
有实数根,则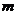 的取值范围是
(
)
的取值范围是
(
)
A.m≥-l B.m<
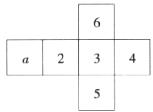
8.如图是一个正方体纸盒的展开图,每个面内都标注了字母或数字,则面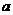 在展开前所对的面的数字是
( )
在展开前所对的面的数字是
( )
A.2 B.
9.如图,⊙I是△ABC的内切圆,D,E,F为三个切点,若∠DEF=52°,则∠A的度数为 ( )
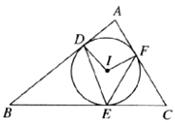
A.76° B.68° C.52° D.38°
10.一辆汽车由A地匀速驶往相距300千米的B地,汽车的速度是100千米/小时,那么汽车距离A地的路程s(千米)与行驶时间t(小时)的函数关系用图象表示为 ( )

二、填空题(本大题共4小题,每小题4分,共16分.请把答案填在题中横线上)
11.分解因式: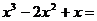 _____________.
_____________.
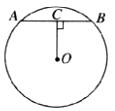
12.如图,在半径为10的⊙O中,如果弦心距OC=6,那么弦AB的长等于_____________.
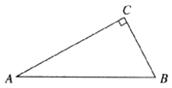
13.如图,在△ABC中,∠C=90°,∠B=60°,AB=10,则BC的长为__________.
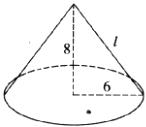
14.如图,圆锥的底面半径为
三、解答题(本大题共6小题,共44分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分6分)
计算: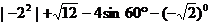
16.(本小题满分6分)
先化简再求值: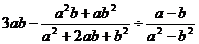 ,其中
,其中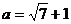 ,
,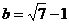 .
.
17.(本小题满分7分)
如图,图1是某中学九年级(一)班全体学生对三种蔬菜的喜欢人数的频数分布直方图.
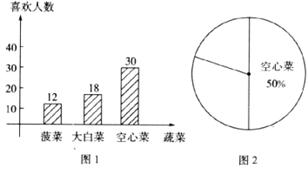
回答下列问题:
(1)九年级(一)班总人数为___________人;
(2)哪种蔬菜的喜欢人数频率最高?并求出该频率;
(3)请根据频数分布直方图中的数据,补全图2中的扇形统计图.
18.(本小题满分7分)
小敏有红色、白色、黄色三件上衣,又有米色、白色的两条裤子.如果她最喜欢的搭配是白色上衣配米色裤子,那么黑暗中,她随机拿出一件上衣和一条裤子,正是她最喜欢搭配的颜色.请你用列表或画树状图,求出这样的巧合发生的概率是多少?
19.(本小题满分8分)
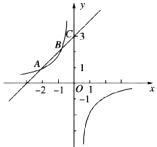
如图,已知反比例函数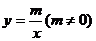 的图象经过点A(-2,1),一次函数
的图象经过点A(-2,1),一次函数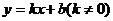 的图象经过点C(0,3)与点A,且与反比例函数的图象相交于另一点B.
的图象经过点C(0,3)与点A,且与反比例函数的图象相交于另一点B.
(1)分别求出反比例函数与一次函数的解析式;
(2)求点B的坐标.
20.(本小题满分10分)
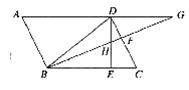
已知如图,□ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G.
(1)求证:AB=BH;
(2)若GA=10,HE=2.求AB的值.
B卷(50分)
四、填空题(本大题共5小题,每小题4分,共20分.请把答案填在题中横 线上)
21.已知 ,
,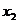 是方程
是方程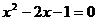 的两个根,则
的两个根,则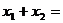 __________.
__________.
22.已知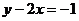 ,则
,则 __________.
__________.
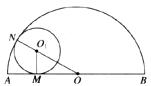
23.如图,半圆O的直径AB=4,与半圆O内切的动圆O1与AB切于点M,点N也为切点,设圆O1的半径为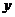 ,AM=
,AM=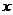 ,则
,则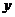 关于
关于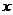 的函数关系式是_____________.
的函数关系式是_____________.
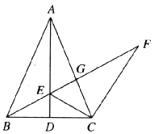
24.如图,在△ABC中,AB=AC,D为BC的中点,E为AD上任意一点,过点C作CF//AB交BE的延长线于点F,BF交AC于点G,连CE,下列结论正确的序号为_____________.
①AD平分∠BAC;②BE=CE;③BE=EG;④若BE=3,GE=2,则GF=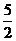 .
.
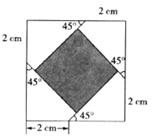
25.现有若干张边长不相等但都大于
五、解答题(本大题共3小题,共30分,解答应写出文字说明、证明过程或演算步骤)
26.(本小题满分8分)
某年7月,甲、乙两工程队承包了A工程,规定若干天内完成.
(1)已知甲单独完成A工程所需时间比规定时间的2倍多4天,乙单独完成A工程所需时间比规定时间的2倍少16天,如果甲、乙两组合做24天完成,那么甲、乙两组合做能否在规定时间内完成?
(2)当甲、乙合做完成A工程的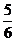 后,两工程队又承包了B工程,此时需抽调一工程队过去,从按时完成A工程考虑,你认为抽调甲、乙哪个最好?请说明理由.
后,两工程队又承包了B工程,此时需抽调一工程队过去,从按时完成A工程考虑,你认为抽调甲、乙哪个最好?请说明理由.
27.(本小题满分10分)
已知:如图,圆内接四边形ABCD的两边AB,DC的延长线相交于点E,DF经过⊙O的圆心,交AB于点F,AB=BE,连接AC,且OD=3,FA=FB=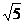 .
.
(1)求证:△DAC∽△DEA;
(2)求出DA,AC的长度.

28.(本小题满分I2分)
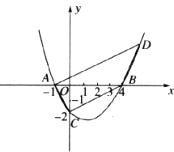
如图,抛物线 与
与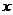 轴交于点A(-1,0),B(4,0),与
轴交于点A(-1,0),B(4,0),与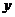 轴交于点C(0,-2).
轴交于点C(0,-2).
(1)求此抛物线的解析式;
(2)若D点在此抛物线上,且AD//CB,在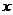 轴上是否存在点E,使得以A,D,E为顶点的三角形与△ABC相似,若存在,求出点E的坐标;若不存在,请说明理由;
轴上是否存在点E,使得以A,D,E为顶点的三角形与△ABC相似,若存在,求出点E的坐标;若不存在,请说明理由;
(3)在(2)的条件下,问在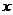 轴下方的抛物线上,是否存在点P使得△APD的面积与四边形ACBD的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
轴下方的抛物线上,是否存在点P使得△APD的面积与四边形ACBD的面积相等?若存在,求出P点坐标;若不存在,请说明理由.