2009年广西河池市初中毕业暨升学统一考试
数学试卷
(考试时间120分钟,满分120分)
一、填空题(本大题共10小题,每小题2分,共20分,请将正确答案填写在题中的横线上.)
1.如果上升
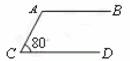
2.如图,已知AB∥CD,则∠A = 度.
3.今年我市初中毕业暨升学统一考试的考生约有35300人,该数据用科学记数法表示为
人.
4.投掷一枚质地均匀的正方体骰子,朝上的一面为6点的概率是 .
5.分解因式: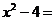 .
.
6.已知一组数据1,a,3,6,7,它的平均数是4,这组数据的众数是 .
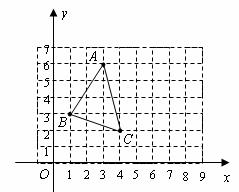
7.如图,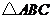 的顶点坐标分别为
的顶点坐标分别为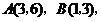
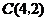 .若将
.若将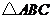 绕
绕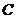 点顺时针旋转
点顺时针旋转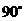 ,得到
,得到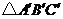 ,则点
,则点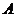 的对应点
的对应点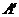 的坐标为
.
的坐标为
.
8.已知关于 、
、 的一次函数
的一次函数 的图象经过平面直角坐标系中的第一、三、四象限,那么
的图象经过平面直角坐标系中的第一、三、四象限,那么 的取值范围是
.
的取值范围是
.
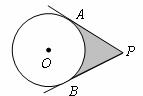
9.如图,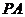 ,
,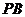 切⊙O于
切⊙O于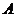 ,
,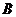 两点,若
两点,若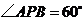 ,⊙O的半径为
,⊙O的半径为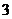 ,则阴影部分的面积为
.
,则阴影部分的面积为
.
10.某小区有一块等腰三角形的草地,它的一边长为 ,面积为
,面积为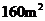 ,为美化小区环境,现要给这块三角形草地围上白色的低矮栅栏,则需要栅栏的长度为 m.
,为美化小区环境,现要给这块三角形草地围上白色的低矮栅栏,则需要栅栏的长度为 m.
二、选择题(本大题共8小题,每小题3分,共24分;在每小题给出的四个选项中,只有一项是正确的,请将正确答案的代号填入题后的括号内,每小题选对得3分,选错、不选或多选均得零分.)
11.下列运算正确的是( )
A. 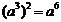 B.
B. 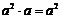 C.
C. 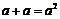 D.
D. 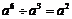
12.下列事件是随机事件的是( )
A.在一个标准大气压下,加热到
B.购买一张福利彩票,中奖
C.有一名运动员奔跑的速度是
D.在一个仅装着白球和黑球的袋中摸球,摸出红球
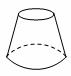
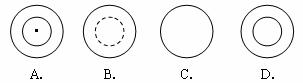
13.下图是圆台状灯罩的示意图,它的俯视图是( )
14.若两圆的半径分别是
A.内切 B.相交 C.外切 D.外离
15.一个不等式的解集为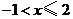 ,那么在数轴上表示正确的是( )
,那么在数轴上表示正确的是( )

16.已知菱形的边长和一条对角线的长均为 ,则菱形的面积为( )
,则菱形的面积为( )
A. 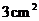 B.
B. 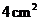 C.
C. 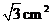 D.
D. 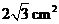
17.如图,A、B是函数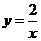 的图象上关于原点对称的任意两点,BC∥
的图象上关于原点对称的任意两点,BC∥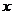 轴,AC∥
轴,AC∥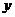 轴,△ABC的面积记为
轴,△ABC的面积记为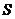 ,则( )
,则( )

A. 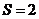 B.
B. 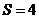 C.
C. D.
D.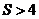
18.如图,在Rt△ABC中,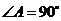 ,AB=AC=
,AB=AC=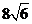 ,点E为AC的中点,点F在底边BC上,且
,点E为AC的中点,点F在底边BC上,且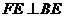 ,则△
,则△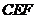 的面积是( )
的面积是( )

A. 16 B. 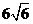 D.
D. 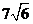
三、解答题 (本大题共8小题,满分76分,解答应写出文字说明、证明过程或演算步骤.)
19.(本小题满分9分)
计算: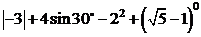
20.(本小题满分9分)
如图,在△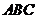 中,∠ACB=
中,∠ACB=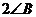 .
.
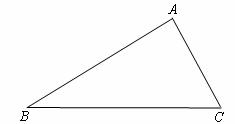
(1)根据要求作图:
① 作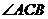 的平分线交AB于D;
的平分线交AB于D;
② 过D点作DE⊥BC,垂足为E.
(2)在(1)的基础上写出一对全等三角形和一对相似比不为1的相似三角形:
△ ≌△ ;△ ∽△ .
请选择其中一对加以证明.
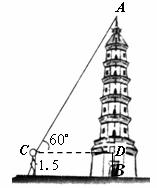
21.(本小题满分8分)
如图,为测量某塔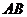 的高度,在离该塔底部
的高度,在离该塔底部 ,目高
,目高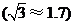 .
.
22.(本小题满分8分)
某校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按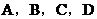 四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
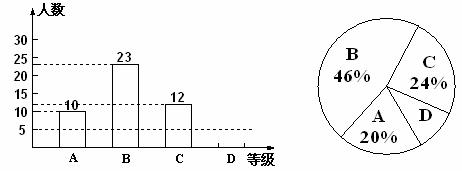
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)样本中D级的学生人数占全班学生人数的百分比是 ;
(3)扇形统计图中A级所在的扇形的圆心角度数是 ;
(4)若该校九年级有500名学生,请你用此样本估计体育测试中A级和B级的学生人数约为 人.
23.(本小题满分10分)
铭润超市用5000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11000元资金购进该品种苹果,但这次的进货价比试销时每千克多了0.5元,购进苹果数量是试销时的2倍.
(1)试销时该品种苹果的进货价是每千克多少元?
(2)如果超市将该品种苹果按每千克7元的定价出售,当大部分苹果售出后,余下的
24.(本小题满分10分)
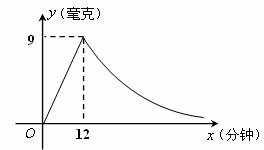
为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量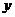 (毫克)与时间
(毫克)与时间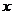 (分钟)成正比例;药物释放完毕后,
(分钟)成正比例;药物释放完毕后,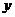 与
与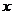 成反比例,如图所示.根据图中提供的信息,解答下列问题:
成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,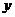 与
与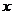 之间的两个函数关系式及相应的自变量取值范围;
之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
25.(本小题满分10分)
如图,在⊙O中,AB为⊙O的直径,AC是弦,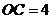 ,
,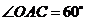 .
.
(1)求∠AOC的度数;
(2)在图1中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;
(3)如图2,一动点M从A点出发,在⊙O上按逆时针方向运动,当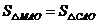 时,求动点M所经过的弧长.
时,求动点M所经过的弧长.
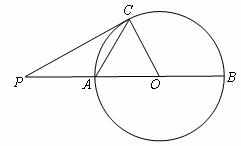

图1 图2
26.(本小题满分12分)
如图,已知抛物线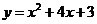 交
交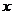 轴于A、B两点,交
轴于A、B两点,交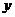 轴于点C,抛物线的对称轴交
轴于点C,抛物线的对称轴交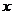 轴于点E,点B的坐标为(
轴于点E,点B的坐标为(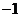 ,0).
,0).
(1)求抛物线的对称轴及点A的坐标;
(2)在平面直角坐标系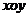 中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
(3)连结CA与抛物线的对称轴交于点D,在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由.
