2009年福建省莆田初中毕业班质量检查
数学试卷
(满分:150分;考试时间:120分钟)
一、细心填一填(本大题共l0小题,每小题4分,共40分.直接把答案填在题中的横线上.)
1.一2的相反数为_________.
2.计算: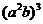 =_________.
=_________.
3.莆田市“十一五”规划明确了今后五年“经济翻番、港城崛起”的奋斗目标,即2010年金市地区生产总值突破800亿元,把800亿元取两个有效数字用科学记数法可表示为______元.
4.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是_________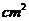 .
.

5.一个圆内接正六边形的边长为2,那么这个正六边形的边心距为_________.
6.袋中装有除颜色外其他完全相同的4个小球,其中3个红色,1个白色.从袋中任意地摸出两个球,这两个球颜色相同的概率是_________.
7.已知⊙ 和⊙
和⊙ 的半径分别是一元二次方程
的半径分别是一元二次方程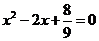 的两根且
的两根且 ,则⊙
,则⊙ 和⊙
和⊙ 的位置关系是_________.
的位置关系是_________.
8.某梯子与地面所成的角α满足45°≤α≤60°时,人可以安全地爬上斜靠在墙面上的梯子的顶端现有―个长
9.正比例函数 与反比例函数
与反比例函数 在同一平面直角坐标系中的图象如 图所示,则当
在同一平面直角坐标系中的图象如 图所示,则当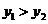 时
时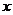 的取值范围是_________.
的取值范围是_________.

10.如图,把矩形ABCD沿EF折叠,使点B落在边AD上的点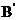 处,点A落在点
处,点A落在点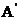 处.若AE=a、AB=b、BF=C,请写出a、b、c之间的一个等量关系_________.
处.若AE=a、AB=b、BF=C,请写出a、b、c之间的一个等量关系_________.

二、精心选一选(本大题共6小题。每小题4分,共24分.每小题给出的四个选项中有且只有一个是正确的。请把正确选项的代号写在题后的括号内,答对的得4分;答错、不答或答案超过一个的一律得0分.)
11.若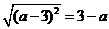 ,则
,则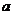 与3的大小关系是( )
与3的大小关系是( )
A. B.
B.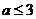 C.
C. D.
D.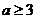
12.莆田市某一周的日最高气温(℃)分别为:25、28、30、29、31、32、28.则该周的日最高气温的平均数和中位数分别是( )
A.28、29 B.29、
13.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形.
C.对角线互楣垂直且相等的四边形是正方形.
D.对角线互相平分的四边形是平行四边形.
14.一个圆锥的侧面展开图是一个半圆,则此圆锥母线长与底面半径之比为( )
A.2:1 B.1:
15.二次函数 的图象如何平移得到
的图象如何平移得到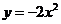 的图像( )
的图像( )
A.向左平移1个单位,再向上平移3个单位.
B.向右平移1个单位,再向上平移3个单位.
C.向左平移1个单位,再向下平移3个单位.
D.向右平移1个单位,再向下平移3个单位。
16.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为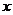 ,△ABP的面积为y,如果y关于
,△ABP的面积为y,如果y关于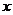 的函数图象如图2所示,则矩形ABCD的面积是( )
的函数图象如图2所示,则矩形ABCD的面积是( )

A.10 B.
二、耐心填一填(本犬题共9小题。共86分.解答应写出必要的文字说明、证明过程或演算步骤。)
17.(8分)计算:

18.(8分)先化简。再求值:
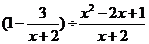 ,其中
,其中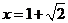 。
。
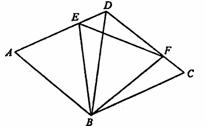
19.(8分)如图菱形ABCD的边长为2,对角线BD=2,E、F分别是AD、CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDF≌△BCF;
(2)判断△BEF的形状,并说明理由。同时指出△BCF是由△BDE经过如何变换得到?
20.(8分)△ABC在方格中的位置如图所示。
(1)请在方格纸上建立平面直角坐标系,使得A、B两点的坐标分别为A(2,一1)、B(1,一4)。并求出C点的坐标;
(2)作出△ABC关于横轴对称的△ ,再作出△ABC以坐标原点为旋转中心、旋转180°后的△
,再作出△ABC以坐标原点为旋转中心、旋转180°后的△ ,并写出
,并写出 、
、 两点的坐标.
两点的坐标.

21.(8分)某校九年级(1)班课题研究小组对本校九年级全体同学的体育达标(体育成绩60分以上,含60分)情况进行调查.他们对本班50名同学的体育达标情况和其余班级同学的体育达标 情况分别进行调查,数据统计结果如下:
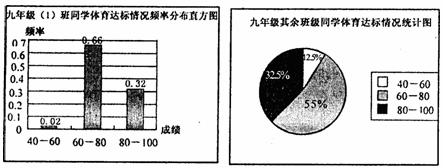
说明:每组成绩的取值范围中,含最低值,不合最高值.
根据以上统计图,请解答下面问题:
(1)九年级(1)班同学体育达标率和九年级其余班级同学体育达标率各是多少?
(2)如果全年段同学的体育达标率不低于90%,则全年段同学人数不超过多少人?
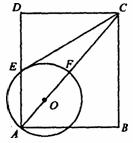
22.(10分)已知,如图在矩形ABCD中,点O在对角线AC上,以 OA长为半径的圆0与AD、AC分别交于点E、F。∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=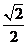 ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
23.(10分)某工厂计划招聘A、B两个工种的工人共120人,A、B两个工种的工人月工资分别为800元和1000元.
(1)若某工厂每月支付的工人工资为110000元,那么A、B两个工种的工人各招聘多少人?设招聘A工种的工人x人。根据题设完成下列表格,并列方程求解.
(2)若要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的工人多少人时,可使工厂每月支付的工人工资最少?
工人每月工资(元)
招聘人数
工厂应付工人的月工资(元)
A
x
B
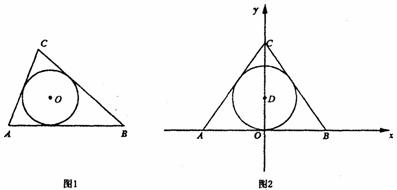
24.(12分)(1)已知,如图l,△ABC的周长为 ,面积为S,其内切圆圆心为O,半径为r,求证:
,面积为S,其内切圆圆心为O,半径为r,求证: ;
;
(2)已知,如图2,△ABC中,A、B、C三点的坐标分别为A(一3,0)、B(3,0)、C(0,4).若△ABC内心为D。求点D坐标;
(3)与三角形的一边和其他两边的延长线相切的圆,叫旁切圆,圆心叫旁心.请求出条件(2)中的△ABC位于第一象限的旁心的坐标。
25.(14分)已知,如图抛物线 与y轴交于C点,与x轴交于A、B两点,A点在B点左侧。点B的坐标为(1,0),OC=30B.
与y轴交于C点,与x轴交于A、B两点,A点在B点左侧。点B的坐标为(1,0),OC=30B.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值:
(3)若点E在x轴上,点P在抛物线上。是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
