2009年湖北省咸宁市初中毕业生学业考试
数学试卷
考生注意:
1.本试卷共8页,24小题;满分120分;考试用时120分钟.
2.答题前,请将密封线内的项目填写清楚、完整.沉着、冷静,相信你能行!
参考公式:抛物线 (
( 是常数,
是常数, )的顶点坐标是
)的顶点坐标是 .
.
一、精心选一选(本大题共8小题,每小题3分,满分24分)每小题给出的4个选项中只有一个符合题意,请将所选选项的字母代号写在题后的括号内.
1.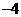 的绝对值是(
)
的绝对值是(
)
A.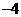 B.
B.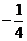 C.4 D.
C.4 D.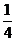
2.
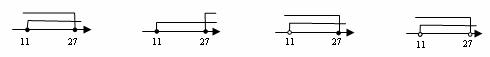
A. B. C. D.
3.下列运算正确的是( )
A.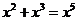 B.
B.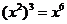
C.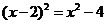 D.
D.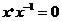
4.温家宝总理在2009年政府工作报告中提出,今后三年内各级政府拟投入医疗卫生领域的资金将达到8500亿元人民币,用科学记数表表示“8500亿”为( )
A.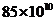 B.
B.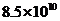 C.
C.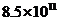 D.
D.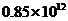
5.方程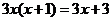 的解为( )
的解为( )
A.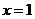 B.
B.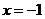
C.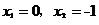 D.
D.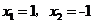
6.下列说法正确的是( )
A.某一种彩票中奖概率是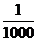 ,那么买1000张该种彩票就一定能中奖
,那么买1000张该种彩票就一定能中奖
B.打开电视看CCTV―5频道,正在播放NBA篮球比赛是必然发生的事件
C.调查某池塘中现有鱼的数量,宜采用抽样调查
D.极差不能反映数据的波动情况
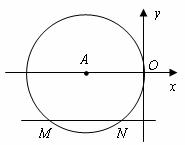
7.如图,在平面直角坐标系中,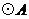 与
与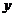 轴相切于原点
轴相切于原点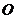 ,平行于
,平行于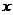 轴的直线交
轴的直线交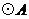 于
于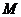 、
、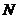 两点,若点
两点,若点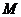 的坐标是
的坐标是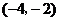 ,则点
,则点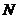 的坐标为( )
的坐标为( )
A.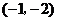 B.
B.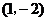
C.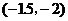 D.
D.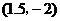
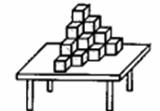
8.如图,桌面上的模型由20个棱长为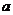 的小正方体组成,现将该模型露在外面的部分涂上涂料,则涂上涂料部分的总面积为( )
的小正方体组成,现将该模型露在外面的部分涂上涂料,则涂上涂料部分的总面积为( )
A.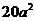 B.
B.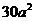 C.
C.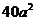 D.
D.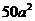
二、细心填一填(本大题共8小题,每小题3分,满分24分)请把答案直接写在题中的横线上.
9.在函数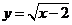 中,自变量
中,自变量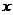 的取值范围是____________.
的取值范围是____________.
10.分式方程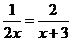 的解是_____________.
的解是_____________.
11.同时掷两枚硬币,两枚硬币全部正面朝上的概率为____________.
12.已知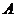 、
、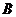 是抛物线
是抛物线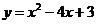 上位置不同的两点,且关于抛物线的对称轴对称,则点
上位置不同的两点,且关于抛物线的对称轴对称,则点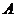 、
、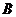 的坐标可能是_____________.(写出一对即可)
的坐标可能是_____________.(写出一对即可)
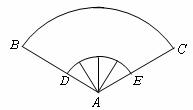
13.为庆祝祖国六十华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条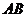 、
、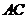 夹角为
夹角为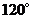 ,
,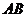 的长为
的长为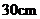 ,贴布部分
,贴布部分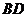 的长为
的长为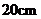 ,则贴布部分的面积约为____________
,则贴布部分的面积约为____________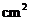 .(
.(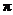 取3)
取3)
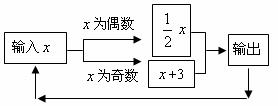
14.如图所示的运算程序中,若开始输入的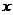 值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,……第2009次输出的结果为___________.
值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,……第2009次输出的结果为___________.
15.反比例函数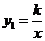 与一次函数
与一次函数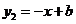 的图象交于点
的图象交于点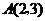 和点
和点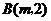 .由图象可知,对于同一个
.由图象可知,对于同一个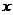 ,若
,若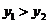 ,则
,则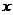 的取值范围是______________.
的取值范围是______________.
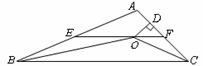
16.如图,在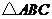 中,
中,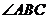 和
和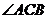 的平分线相交于点
的平分线相交于点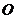 ,过点
,过点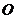 作
作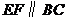 交
交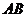 于
于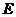 ,交
,交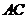 于
于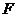 ,过点
,过点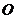 作
作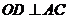 于
于 .下列四个结论:
.下列四个结论:
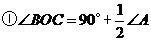 ;
;
②以 为圆心、
为圆心、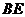 为半径的圆与以
为半径的圆与以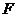 为圆心、
为圆心、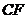 为半径的圆外切;
为半径的圆外切;
③设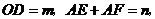 则
则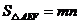 ;
;
④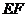 不能成为
不能成为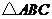 的中位线.
的中位线.
其中正确的结论是_____________.(把你认为正确结论的序号都填上)
三、专心解一解(本大题共8小题,满分72分)请认真审题,冷静思考.解答题应写出文字说明、证明过程或演算步骤.
17.(本题满分6分)
先将代数式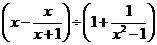 化简,再从
化简,再从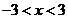 的范围内选取一个合适的整数
的范围内选取一个合适的整数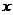 代入求值.
代入求值.
18.(本题满分8分)
某企业开发的一种罐装饮料,有大、小件两种包装,3大件4小件共装120缺罐,2大件3小件共装84罐.每大件与每小件各装多少罐?
19.(本题满分8分)
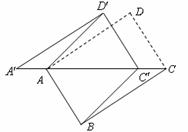
如图,将矩形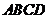 沿对角线
沿对角线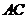 剪开,再把
剪开,再把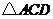 沿
沿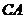 方向平移得到
方向平移得到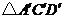 .
.
(1)证明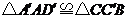 ;
;
(2)若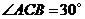 ,试问当点
,试问当点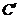 在线段
在线段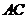 上的什么位置时,四边形
上的什么位置时,四边形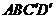 是菱形,并请说明理由.
是菱形,并请说明理由.
20.(本题满分9分)
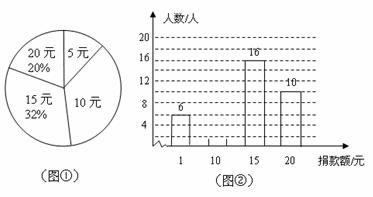
在一次“爱心助学”捐款活动中,九(1)班同学人人拿出自己的零花钱,踊跃捐款,学生捐款额有5元、10元、15元、20元四种情况.根据统计数据绘制了图①和图②两幅尚不完整的统计图.
(1)该班共有_____________名同学,学生捐款的众数是______________;
(2)请你将图②的统计图补充完整;
(3)计算该班同学平均捐款多少元?
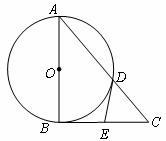
21.(本题满分9分)
如图, 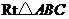 中,
中,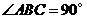 ,以
,以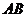 为直径的
为直径的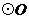 交
交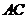 于点
于点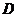 ,过点
,过点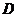 的切线交
的切线交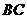 于
于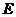 .
.
(1)求证: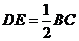 ;
;
(2)若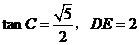 ,求
,求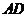 的长.
的长.
22.(本题满分10分)
问题背景:
在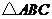 中,
中,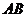 、
、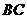 、
、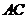 三边的长分别为
三边的长分别为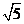 、
、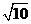 、
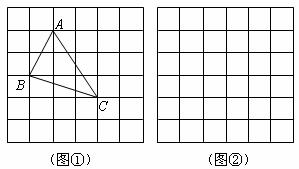
、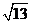 ,求这个三角形的面积。小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点
,求这个三角形的面积。小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点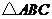 (即
(即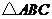 三个顶点都在小正方形的顶点处),如图
三个顶点都在小正方形的顶点处),如图 所示.这样不需求
所示.这样不需求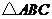 的高,而借用网格就能计算出它的面积.
的高,而借用网格就能计算出它的面积.
(1)请你将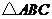 的面积直接填写在横线上.__________________
的面积直接填写在横线上.__________________
思维拓展:
(2)我们把上述求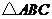 面积的方法叫做构图法.若
面积的方法叫做构图法.若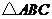 三边的长分别为
三边的长分别为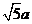 、
、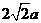 、
、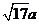 (
(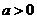 ),请利用图
),请利用图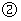 的正方形网格(每个小正方形的边长为
的正方形网格(每个小正方形的边长为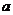 )画出相应的
)画出相应的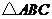 ,并求出它的面积.
,并求出它的面积.
探索创新:
(3)若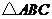 三边的长分别为
三边的长分别为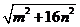 、
、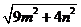 、
、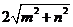 (
(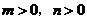 ,且
,且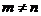 ),试运用构图法求出这三角形的面积.
),试运用构图法求出这三角形的面积.
23.(本题满分10分)
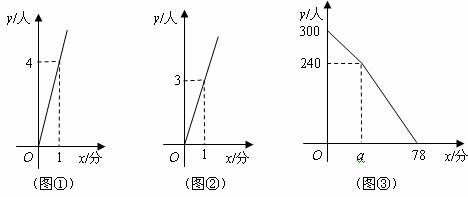
某车站客流量大,旅客往往需长时间排队等候购票.经调查统计发现,每天开始售票时,约有300名旅客排队等候购票,同时有新的旅客不断进入售票厅排队等候购票,新增购票人数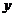 (人)与售票时间
(人)与售票时间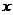 (分)的函数关系如图
(分)的函数关系如图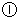 所示;每个售票窗口票数
所示;每个售票窗口票数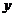 (人)与售票时间
(人)与售票时间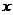 (分)的函数关系如图
(分)的函数关系如图 所示.某天售票厅排队等候购票的人数
所示.某天售票厅排队等候购票的人数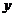 (人)与售票时间
(人)与售票时间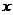 (分)的函数关系如图
(分)的函数关系如图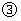 所示,已知售票的前
所示,已知售票的前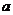 分钟开放了两个售票窗口.
分钟开放了两个售票窗口.
(1)求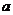 的值;
的值;
(2)求售票到第60分钟时,售票厅排队等候购票的旅客人数;
(3)该车站在学习实践科学发展观的活动中,本着“以人为本,方便旅客”的宗旨,决定增设售票窗口.若要在开始售票后半小时内让所有排队购票的旅客都能购到票,以便后来到站的旅客能随到随购,请你帮助计算,至少需同时开放几个售票窗口?
24.(本题满分12分)
如图①,在平面直角坐标系中,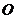 为坐标原点,边长为
为坐标原点,边长为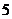 的正三角形
的正三角形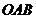 的
的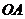 边在
边在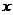 轴的正半轴上.点
轴的正半轴上.点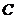 、
、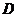 同时从点
同时从点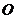 出发,点
出发,点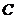 以1单位长/秒的速度向点
以1单位长/秒的速度向点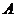 运动,点
运动,点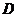 为2个单位长/秒的速度沿折线
为2个单位长/秒的速度沿折线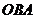 运动.设运动时间为
运动.设运动时间为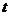 秒,
秒,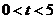 .
.
(1)当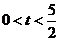 时,证明
时,证明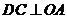 ;
;
(2)若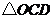 的面积为
的面积为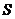 ,求
,求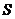 与
与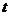 的函数关系式;
的函数关系式;
(3)以点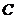 为中心,将
为中心,将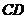 所在的直线顺时针旋转60°交
所在的直线顺时针旋转60°交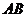 边于点
边于点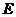 ,若以
,若以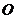 、
、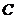 、
、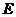 、
、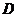 为顶点的四边形是梯形,求点
为顶点的四边形是梯形,求点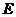 的坐标.
的坐标.