2009年江西省中等学校招生考试
数学试卷
说明:
1.本卷共有六个大题,25个小题,全卷满分120分,考试时间120分钟.
2.本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上作答,否则不给分.
一、选择题(本大题共10小题,每小题3分,共30分)
1. 的绝对值是(
)
的绝对值是(
)
A.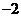 B.
B.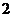 C.
C. D.
D.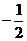
2.化简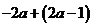 的结果是( )
的结果是( )
A.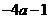 B.
B.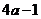 C.
C. D.
D.
3.如图,直线

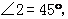 则
则 的度数为( )
的度数为( )

A.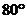 B.
B.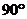 C.
C. D.
D.
4.方程组 的解是( )
的解是( )
A. B.
B.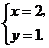 C.
C. D.
D.
5.在下列四种图形变换中,本题图案不包含的变换是( )

A.位似 B.旋转 C.轴对称 D.平移
6.某中学篮球队12名队员的年龄情况如下:
年龄(单位:岁)
14
15
16
17
18
人数
1
4
3
2
2
则这个队队员年龄的众数和中位数分别是( )
A. B.
B. C.
C. D.
D.
7.如图,已知 那么添加下列一个条件后,仍无法判定
那么添加下列一个条件后,仍无法判定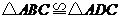 的是( )
的是( )
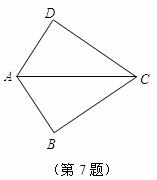
A.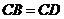 B.
B.
C. D.
D.
8.在数轴上,点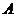 所表示的实数为3,点
所表示的实数为3,点 所表示的实数为
所表示的实数为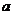 ,⊙A的半径为2.下列说法中不正确的是(
)
,⊙A的半径为2.下列说法中不正确的是(
)
A.当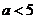 时,点
时,点 在⊙A内
在⊙A内
B.当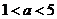 时,点
时,点 在⊙A内
在⊙A内
C.当 时,点
时,点 在⊙A外
在⊙A外
D.当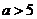 时,点
时,点 在⊙A外
在⊙A外
9.如图,分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图,则组成这个几何体的小正方体的个数是( )

A.2个或3个 B.3个或4个 C.4个或5个 D.5个或6个
10.为了让江西的山更绿、水更清,2008年省委、省政府提出了确保到2010年实现全省森林覆盖率达到63%的目标,已知2008年我省森林覆盖率为60.05%,设从2008年起我省森林覆盖率的年平均增长率为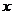 ,则可列方程(
)
,则可列方程(
)
A. B.
B.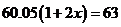
C.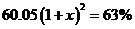 D.
D.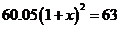
二、填空题(本大题共6小题,每小题3分,共18分)
11.写出一个大于1且小于4的无理数 .
12.选做题(从下面两题中只选做一题,如果做了两题的,只按第(1)题评分).
(Ⅰ)方程 的解是
.
的解是
.
(Ⅱ)用计算器计算: .(结果保留三个有效数字)
.(结果保留三个有效数字)
13.用直径为 的半圆形铁皮围成一个圆锥的侧面(不计接缝部分),则此圆锥的底面半径是
的半圆形铁皮围成一个圆锥的侧面(不计接缝部分),则此圆锥的底面半径是
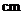 .
.
14.不等式组 的解集是
.
的解集是
.
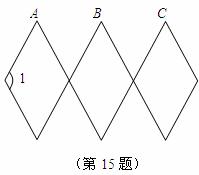
15.如图,一活动菱形衣架中,菱形的边长均为 若墙上钉子间的距离
若墙上钉子间的距离 则
则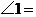 度.
度.
16.函数 的图象如图所示,则结论:
的图象如图所示,则结论:
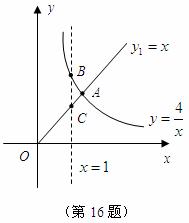
①两函数图象的交点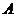 的坐标为
的坐标为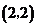 ;
;
②当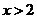 时,
时, ;
;
③当 时,
时,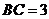 ;
;
④当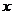 逐渐增大时,
逐渐增大时,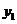 随着
随着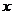 的增大而增大,
的增大而增大, 随着
随着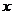 的增大而减小.其中正确结论的序号是
.
的增大而减小.其中正确结论的序号是
.
三、(本大题共3个小题,第17小题6分,第18、19小题各7分,共20分)
17.计算: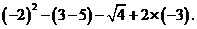
18.先化简,再求值:
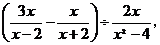 其中
其中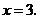
19.某市今年中考理、化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试.小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(1)用“列表法”或“树状图法”表示所有可能出现的结果;
(2)小刚抽到物理实验B和化学实验F(记作事件M)的概率是多少?
四、(本大题共2个小题,每小题8分,共16分)
20.经市场调查,某种优质西瓜质量为(5±0.25)kg的最为畅销.为了控制西瓜的质量,农科所采用A、B两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取20颗,记录它们的质量如下(单位:kg):
A:4.1 4.8 5.4 4.9 4.7 5.0 4.9 4.8 5.8 5.2
5.0 4.8 5.2 4.9 5.2 5.0 4.8 5.2 5.1 5.0
B:4.5 4.9 4.8 4.5 5.2 5.1 5.0 4.5 4.7 4.9
5.4 5.5 4.6 5.3 4.8 5.0 5.2 5.3 5.0 5.3
(1)若质量为(5±0.25)kg的为优等品,根据以上信息完成下表:
优等品数量(颗)
平均数
方差
A
4.990
0.103
B
4.975
0.093
(2)请分别从优等品数量、平均数与方差三方面对A、B两种技术作出评价;从市场销售的角度看,你认为推广哪种种植技术较好.
21.某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段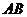 、
、 分别表示父、子俩送票、取票过程中,离体育馆的路程
分别表示父、子俩送票、取票过程中,离体育馆的路程 (米)与所用时间
(米)与所用时间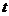 (分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
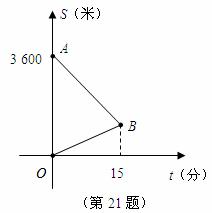
(1)求点 的坐标和
的坐标和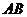 所在直线的函数关系式;
所在直线的函数关系式;
(2)小明能否在比赛开始前到达体育馆?
五、(本大题共2小题,第22小题8分,第23小题9分,共17分)
22.如图,已知线段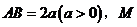 是
是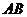 的中点,直线
的中点,直线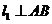 于点
于点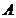 ,直线
,直线 于点
于点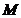 ,点
,点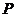 是
是 左侧一点,
左侧一点,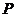 到
到 的距离为
的距离为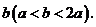
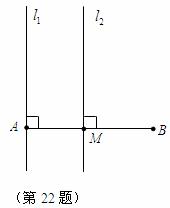
(1)作出点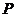 关于
关于 的对称点
的对称点 ,并在
,并在 上取一点
上取一点 ,使点
,使点 、
、 关于
关于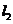 对称;
对称;
(2)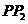 与
与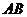 有何位置关系和数量关系?请说明理由.
有何位置关系和数量关系?请说明理由.
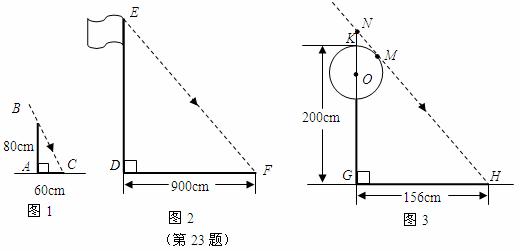
23.问题背景 在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:
甲组:如图1,测得一根直立于平地,长为
乙组:如图2,测得学校旗杆的影长为
丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为
任务要求
(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;
(2)如图3,设太阳光线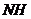 与⊙O相切于点
与⊙O相切于点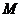 .请根据甲、丙两组得到的信息,求景灯灯罩的半径(友情提示:如图3,景灯的影长等于线段
.请根据甲、丙两组得到的信息,求景灯灯罩的半径(友情提示:如图3,景灯的影长等于线段 的影长;需要时可采用等式
的影长;需要时可采用等式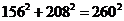 ).
).
六、(本大题共2个小题,第24小题9分,第25小题10分,共19分)
24.如图,抛物线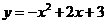 与
与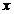 轴相交于
轴相交于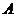 、
、 两点(点
两点(点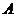 在点
在点 的左侧),与
的左侧),与 轴相交于点
轴相交于点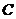 ,顶点为
,顶点为 .
.

(1)直接写出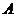 、
、 、
、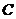 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
(2)连接 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点 ,点
,点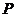 为线段
为线段 上的一个动点,过点
上的一个动点,过点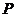 作
作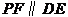 交抛物线于点
交抛物线于点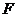 ,设点
,设点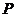 的横坐标为
的横坐标为 ;
;
①用含 的代数式表示线段
的代数式表示线段 的长,并求出当
的长,并求出当 为何值时,四边形
为何值时,四边形 为平行四边形?
为平行四边形?
②设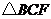 的面积为
的面积为 ,求
,求 与
与 的函数关系式.
的函数关系式.
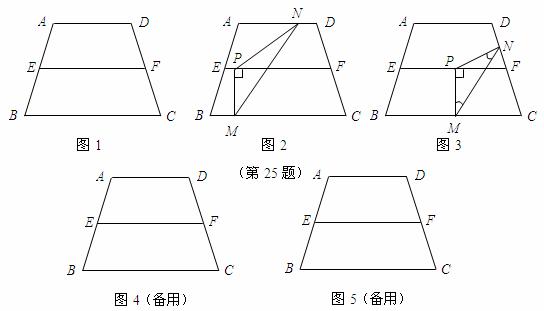
25.如图1,在等腰梯形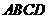 中,
中,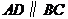 ,
, 是
是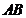 的中点,过点
的中点,过点 作
作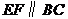 交
交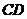 于点
于点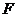 .
.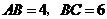 ,
,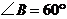 .
.
(1)求点 到
到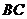 的距离;
的距离;
(2)点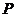 为线段
为线段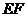 上的一个动点,过
上的一个动点,过 作
作 交
交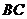 于点
于点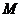 ,过
,过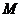 作
作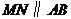 交折线
交折线 于点
于点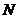 ,连结
,连结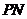 ,设
,设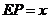 .
.
①当点 在线段
在线段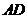 上时(如图2),
上时(如图2), 的形状是否发生改变?若不变,求出
的形状是否发生改变?若不变,求出 的周长;若改变,请说明理由;
的周长;若改变,请说明理由;
②当点 在线段
在线段 上时(如图3),是否存在点
上时(如图3),是否存在点 ,使
,使 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的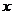 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.