2009年聊城市普通高中招生统一考试
数学试卷
一、选择题(本题共12小题,每小题3分,共36分)
1.计算(-3)2+4的结果是( )
A.-5 B.-
2.如图,数轴上的点P、O、Q、R、S表示某城市一条大街上的五个公交车站点,有一辆公交车距P站点

A.R站点与S站点之间 B.P站点与O站点之间
C.O站点与Q站点之间 D.Q站点与R站点之间
3.在显微镜下,人体内一种细胞的形状可以近似地看成圆,它的半径约为
A.0.78×10
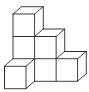
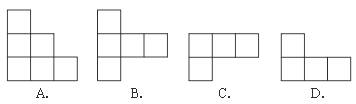
4.如图是由七个相同的小正方体堆成的物体,这个物体的俯视图是( )
5.下列运算正确的是( )
A.
C.(-m4)3=m7
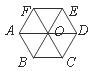
D.m6÷
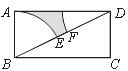
6.如图,在Rt△ABC中,AB=AC,AD⊥BC,垂足为D.E、F分别是CD、AD上的点,且CE=AF.如果∠AED=62º,那么∠DBF=( )
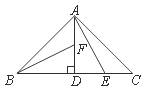
A.62º B.38º C.28º D.26º
7.下列事件中是不确定事件的为( )
A.367人中至少有2人的生日相同
B.今年国庆节这一天,我市的最高气温是
C.掷6枚相同的硬币,3枚正面向上4枚正面向下
D.掷两枚普通的骰子,掷得的点数之和不是奇数就是偶数
8.已知矩形ABCD的边AB=6,AD=8.如果以点A为圆心作⊙A,使B、C、D三点中在圆内和在圆外都至少有一个点,那么⊙A的半径r的取值范围是( )
A.6<r<10 B.8<r<
9.小莹准备用纸板制作一顶圆锥形“圣诞帽”,使“圣诞帽”的底面周长为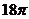 cm,高为
cm,高为
A.72º B.79º C.82º D.85º
10.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于A、B两点.当一次函数的值大于反比例函数的值时,自变量x的取值范围是( )
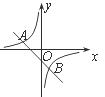
A.-2<x<1 B.0<x<1
C.x<-2和0<x<1 D.-2<x<1和x>1
11.如图,已知矩形ABCD中,AB=8,BC=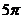 .分别以B、D为圆心,AB为半径画弧,两弧分别交对角线BD于点E、F,则图中阴影部分的面积为(
)
.分别以B、D为圆心,AB为半径画弧,两弧分别交对角线BD于点E、F,则图中阴影部分的面积为(
)
A.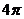 B.
B.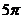 C.
C.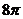 D.
D.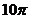
12.在一次“寻宝”游戏中,寻宝人找到了如图所示两个标志点A(2,1)、B(4,-1),这两个标志点到“宝藏”点的距离都是,则“宝藏”点的坐标是( )
A.(,) B.(-2,1)
C.(5,2)或(1,-2) D.(2,-1)或(-2,1)
二、填空题(本题共5小题,每小题3分,共15分)
13.一元二次方程(x+1)(x-1)=2(x+1)的根是 .
14.如图,O是正六边形ABCDEF的中心,图形中可由△OBC绕点O逆时针旋转120º得到的三角形是 .
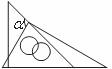
15.一副三角板如图叠放在一起,则图中∠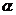 的度数是
.
的度数是
.
16.“五一”节期间,某商场开展购物抽奖活动.抽奖箱内有标号分别为1、2、3、4四个质地、大小相同的小球,顾客从中任意摸出一个球,然后放回,摇匀后再摸出一个球.如果两次摸出的球的标号之和为“
17.如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为 .

三、解答题(本题共8小题,共69分)
18.(6分)解方程:+=1.
19.(7分)如图,某住宅楼进入地下储藏室的坡道AB的长为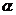 的度数(精确到1º).
的度数(精确到1º).
成绩(米)
…
20.(8分)“立定跳远”是我市初中毕业生体育测试项目之一.测试时,记录下学生立定跳远的成绩,然后按照评分标准转化为相应的分数,满分10分.其中男生立定跳远的评分标准如下:
1.80~1.86
1.86~1.94
1.94~2.02
2.02~2.18
2.18~2.34
2.34~
得分(分)
…
5
6
7
8
9
10
注:成绩栏里的每个范围,含最低值,不含最高值.
某校九年级有480名男生参加立定跳远测试,现从中随机抽取10名男生测试成绩(单位:分)如下:
1.96 2.38 2.56 2.04 2.34 2.17 2.60 2.26 1.87 2.32
请完成下列问题:
(1)求这10名男生立定跳远成绩的极差和平均数;
(2)求这10名男生立定跳远得分的中位数和众数;
(3)如果将9分(含9分)以上定为“优秀”,请你估计这480名男生中得优秀的人数.
21.(8分)今年2月份,电脑被列为国家惠农政策的“家电下乡”商品,小亮家在这个月买了一台电脑和一套沙发共消费4560元.购买这台电脑享受政府补贴13%(即电脑销售价格的13%由政府支付),沙发价格也比上月降价10%,这样小亮家购买这两种商品比上月购买少花640元.小亮家购买电脑和沙发各消费多少元?
22.(8分)如图,在△ABC中,点O是AC边上的一个动点,过点O作MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OC=EF;
(2)当点O位于AC边的什么位置时,四边形AECF是矩形?并给出证明.
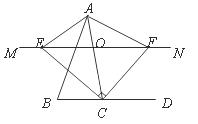
23.(10分)徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出
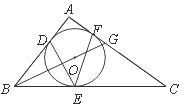
24.(10分)如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DEF=45º.连接BO并延长交AC于点G,AB=4,AG=2.
(1)求∠A的度数;(2)求⊙O的半径.
25.(12分)已知正方形ABCD的边长与Rt△PQR的直角边PQ的长均为
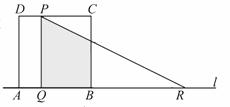
(1)当t=3s时,求S的值;
(2)求S与t之间的函数关系式,并写出自变量t的取值范围;
(3)写出t为何值时,重叠部分的面积S有最大值,最大值是多少?