2008-2009学年度聊城市临清第二学期八年级期中考试
数学试卷
(时间90分钟,满分120分)
一、选择题(本题共12个小题,每小题4分,共48分。在每小题给出的四个选项中,只有一项符合题目要求。)
1.下列各式: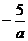 ,
, ,
,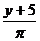 ,
,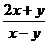 ,
,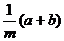 ,
,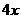 中,分式共有( )个
中,分式共有( )个
A.2 B.
2.若点(-4,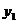 ),(2,
),(2,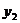 )都在直线
)都在直线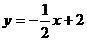 上,则
上,则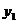 和
和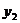 的大小关系为
的大小关系为
A.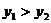 B.
B.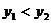 C.
C.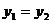 D.不能比较
D.不能比较
3.人体内某种细胞的直径约为0.000
A.0.156× m B.0.156×105m C.1.56×10
m B.0.156×105m C.1.56×10 m D.1.56×106m
m D.1.56×106m
4.下列命题是假命题的是
A.对顶角一定相等
B.全等三角形对应角相等
C.两边及一角对应相等的两个三角形全等
D.两边及第三边上的中线对应相等的两个三角形全等
5.计算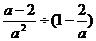 的结果是
的结果是
A.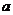 B.
B.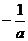 C.
C.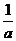 D.
D.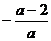
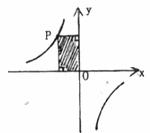
6.如图,点P是反比例函数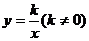 图象上的一点,若图中阴影矩形的面积是6,则此函数关系式为
图象上的一点,若图中阴影矩形的面积是6,则此函数关系式为
A.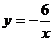 B.
B. C.
C.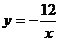 D.
D.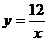
7.将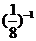 、
、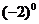 、
、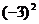 这三个数从小到大排列起来应是
这三个数从小到大排列起来应是
A.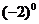 <
<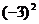 <
<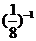 B.
B.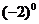 <
<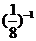 <
<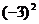
C.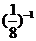 <
<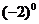 <
<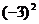 D.
D.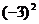 <
<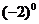 <
<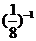
8.关于函数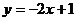 ,下列说法正确的是
,下列说法正确的是
A.图象必过点(-2,4) B.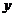 随
随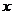 的增大而增大
的增大而增大
C.当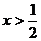 时,
时,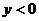 D.图象过一、二、三象限
D.图象过一、二、三象限
9.下列说法正确的是
A.解分式方程一定会产生增根 B.方程 的根为
的根为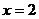
C.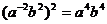 D.无论
D.无论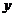 为何值,分式
为何值,分式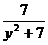 总有意义
总有意义
10.如图,点D在AB上,点E在AC上,且∠B=∠C,那么补充下列一个条件后仍无法判定△ABE≌△ACD的是
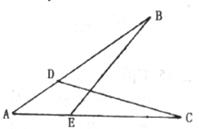
A.BE=CD B.AB=AC C.∠AEB=∠ADC D.AD=AE
11.如图,函数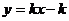 和
和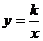 (
(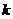 均不为0)的图象大致是
均不为0)的图象大致是
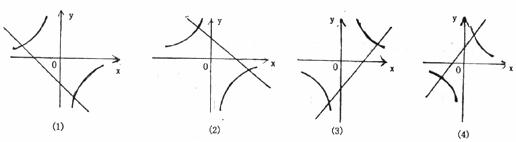
A.(1)或(3) B.(2)或(3) C.(2)或(4) D.(1)或(4)
12.“龟兔赛跑”讲述了这样一个故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到了终点……,若用s1、s2分别表示乌龟和兔子所行的路程,t为时间,则上述图象与故事情节大致吻合的是

二、填空题(每小题4分,共20分)
13.若分式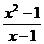 的值为0,则
的值为0,则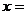 ________。
________。
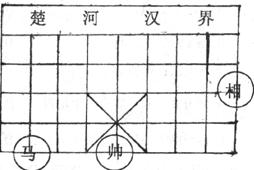
14.中国象棋棋盘中蕴含着直角坐标系,如图是中国象棋棋盘的一半,若图中“帅”位于点(0,0),“马”位于点(-3,0),则“相”所在的点的坐标可表示为___________。
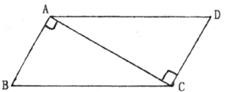
15.如图所示,BA⊥AC于A,DC⊥AC于C,若需再添加一个条件使△ABC≌△CDA,则在以下条件:①AB=DC,②BC=DA,③∠BCA=∠DAC,④∠B =∠D中可行的条件有____________(填序号).
16.若解关于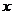 的方程
的方程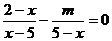 时有增根,则
时有增根,则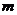 的值为____________.
的值为____________.
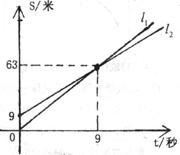
17.如图,射线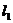 ,
,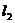 分别表示两位同学在某一时间内骑车运动的一次函数图象,图中s表示骑车运动的路程(米),
分别表示两位同学在某一时间内骑车运动的一次函数图象,图中s表示骑车运动的路程(米),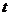 表示骑车运动的时间(秒)。已知甲的速度比乙快,则下列说法:①射线
表示骑车运动的时间(秒)。已知甲的速度比乙快,则下列说法:①射线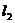 表示甲骑车的路程与时间的关系图象;②甲的速度比乙快l米/秒;③甲让乙先行了9米;④乙比甲早出发了1.5秒;⑤甲出发9秒钟时追上乙。其中,正确的说法是__________ (填序号).
表示甲骑车的路程与时间的关系图象;②甲的速度比乙快l米/秒;③甲让乙先行了9米;④乙比甲早出发了1.5秒;⑤甲出发9秒钟时追上乙。其中,正确的说法是__________ (填序号).
三、解答题(本题共6个小题,共52分。解答应写出必要的文字说明、证明过程或推演步骤。)
18.(本题满分7分)
先化简,再求值: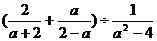 ,其中
,其中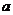 =3。
=3。
19.(本题满分7分)
已知 与
与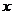 成正比,且当
成正比,且当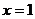 时,
时,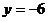 。
。
(1)求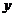 与
与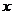 间的函数关系式;
间的函数关系式;
(2)若点Q(m,2)在这个函数图象上,求Q坐标。
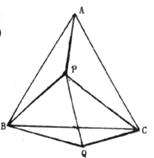
20.(本题满分10分)如图,P是等边△ABC内一点,连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ。
(1)观察并猜想AP和CQ的大小关系,并证明你的结论;
(2)若PA=3,PB=4,PC=5,试判断△PQC的形状,并说明理由.
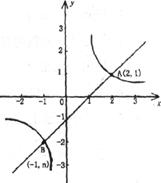
21.(本题满分10分)如图,一次函数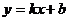 和反比例函数
和反比例函数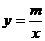 的图象交于A(2,1)、B(-1,n)两点。
的图象交于A(2,1)、B(-1,n)两点。
(1)利用图中已知条件,求这两个函数的表达式;
(2)根据图象回答,当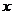 为何值时,一次函数的值大于反比例函数的值(直接写出即可);
为何值时,一次函数的值大于反比例函数的值(直接写出即可);
(3)连接AO、BO,求△AOB的面积.
22.(本题满分8分)列方程解应用题:一项工程限期完成,甲队独做正好按期完成,乙队独做则需延期3天才能完成。现两队合作2天后,再由乙队独做余下工程,也正好按期完成。请你计算一下此工程的规定期限是几天?
23.(本题满分10分)
某电视机厂厂长到一印刷厂印制电视机产品宣传材料,该印刷厂对印刷份数在800份以上(含800份)的客户有两种收费方案。甲方案:每份材料收l元印制费,另收1500元制版费;乙方案:每份材料收2.5元印制费,不收制版费。
(1)请分别写出两种方案中的收费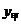 、
、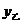 (元)与印制数量
(元)与印制数量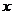 (份)之间的函数关系式,并分别注明自变量取值范围;
(份)之间的函数关系式,并分别注明自变量取值范围;
(2)请你帮忙分析一下,选择哪种方案电视机厂花费较少?并说明理由.