2008-2009学年度菏泽市定陶县第二学期九年级期中学业水平测试
数学试卷
一、精挑细选,火眼金睛(每小题3分,共36分)
1.如下图,给出了过直线外一点作已知直线的平行线的方法,其依据是
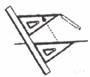
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
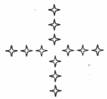
2.下列基本图形中,经过平移、旋转或轴对称变换后,不能得到右图的是

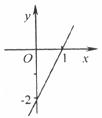
3.已知一次函数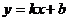 的图像如下图所示,当
的图像如下图所示,当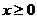 时,
时,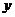 的取值范围是
的取值范围是
A.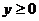 B.
B.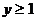 C.
C.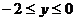 D.
D.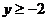
4.如下图,冰淇淋蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积(接缝忽略不计)是
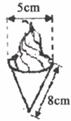
A.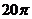 cm2 D.
cm2 D.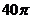 cm2
cm2
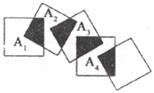
5.下列运算中,正确的是
A.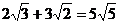 B.
B.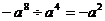
C.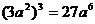 D.
D.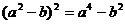
6.已知一次函数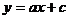 与
与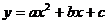 ,它们在同一坐标系内的大致图像是
,它们在同一坐标系内的大致图像是
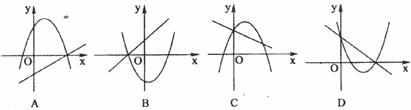
7.由几个相同的小正方体搭成的几何体的三视图如下图所示,则搭成的这个几何体的小正方形的个数为

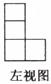
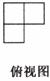
A.4 B.
8.如图,△ABC是不等边三角形,DE=BC,以点D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形可以作出
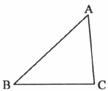

A.2个 B.4个 C.6个 D.8个
9.二次函数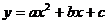 的图像如图所示,那么下列四个结论:①
的图像如图所示,那么下列四个结论:①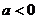 ;②
;②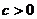 ;③
;③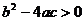 ;④
;④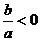 中,正确的结论有
中,正确的结论有
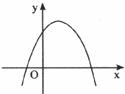
A.1个 B.2个 C.3个 D.4个
10.在Rt△ABC中,若∠C=90°,AB=2,BC=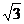 ,则
,则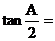
A.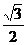 B.
B.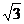 C.
C.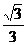 D.
D.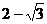
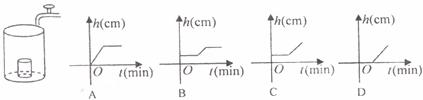
11.将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如下图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图像大致为
12.如下图,在平面直角坐标系中,点P在第一象限内,⊙P与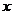 轴相切于点Q,与
轴相切于点Q,与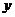 轴交于M(0,2),N(0,8)两点,则点P的坐标为
轴交于M(0,2),N(0,8)两点,则点P的坐标为
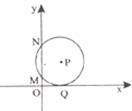
A.(5,3) B.(3,5) C.(5,4) D.(4,5)
二、认真填写,试一试自己的身手(每小题3分,共36分)
13.分解因式: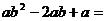 ___________。
___________。
14.函数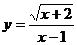 中,自变量
中,自变量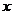 的取值范围是___________。
的取值范围是___________。
15.某商店老板将一件进价为800元的商品先提价50%,再打8折卖出,则卖出这件商品所获利润是___________元。
16.李好在六月连续几天同一时刻观察电表显示的度数,记录如下:
日期
1号
2号
3号
4号
5号
6号
7号
8号
…
30号
电表显示(度)
120
123
127
132
138
141
145
148
…
估计李好家六月份总用电量是___________。
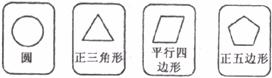
17.有四张背面相同的纸牌,其正面分别画有四个不同的几何图形(如下图)。小华将这4张纸牌背面朝上洗匀后摸出一张,则摸出纸牌牌面图形为中心对称图形的概率为_____。
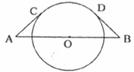
18.如下图,AB=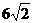 ,O为AB的中点,AC、BD都是半径为3的⊙O的切线,C、D为切点,则弧CD的长为___________。
,O为AB的中点,AC、BD都是半径为3的⊙O的切线,C、D为切点,则弧CD的长为___________。
19.如下图,将 个边长都为
个边长都为 分别是正方形的中心,则
分别是正方形的中心,则 个这样的正方形重叠部分的面积和为___________。
个这样的正方形重叠部分的面积和为___________。
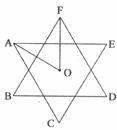
20.如下图,点O是正△ACE和正△BDF的中心,且AE∥BD,则∠AOF=___________。
21.小王与小赵在阳光下行走,小王的身高为
22.下图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是_______。
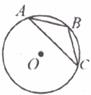
23.如下图,在⊙O中,弦AB=
24.一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分(如下图),则这串珠子被盒子遮住的部分有___________颗。

三、认真解答,一定要细心哟!(共48分)
25.解方程:(每小题4分,共8分)
(1)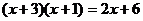
(2) =3
=3
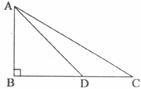
26.(7分)会堂里竖直挂一条幅AB,小刚从与B水平的C点观察,视角∠C=30°,当他沿CB方向前进
27.(8分)某产品每件成本10元,试销阶段每件产品的销售价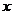 (元)与产品的日销售量
(元)与产品的日销售量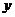 (件)之间的关系如下表:
(件)之间的关系如下表:
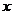 (元)
(元)
15
20
30
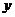 (件)
(件)
25
20
10
若日销售量是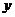 销售价
销售价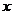 的一次函数。
的一次函数。
(1)求出日销售量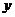 (件)与销售价
(件)与销售价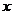 (元)的函数关系式;
(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
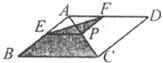
28.(8分)如下图,□ABCD中,E是CD延长线上一点,BE与AD交于点F,DE=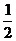 CD。
CD。
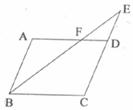
(1)求证:△ABF∽△CEB
(2)若△DEF的面积为2,求四边形BCDF的面积。
29.(8分)今年初,山东省出台了一系列推进素质教育的新举措,提出了“三个还给”,即把时间还给学生,把健康还给学生,把能力还给学生,同学们利用课外活动时间积极参加体育锻炼,小东和小莉就本班同学“我最喜爱的体育项目”进行了一次调查统计,图1和图2是他们通过收集数据后,绘制的两幅不完整的统计图。请你根据图中提供的信息,解答以下问题。

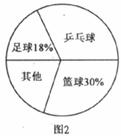
(1)求该班共有多少名学生?
(2)补全条形图;
(3)在扇形统计图中,求出“乒乓球”部分所对应的圆心角的度数;
(4)若全校有1500名学生,请估计“其他”的学生有多少名?
30.(9分)如下图,圆B切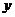 轴于原点O,过定点A(
轴于原点O,过定点A(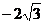 ,0)作圆B切线交圆于点P。已知
,0)作圆B切线交圆于点P。已知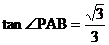 ,抛物线C经过A、P两点。
,抛物线C经过A、P两点。
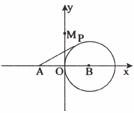
(1)求圆B的半径;
(2)若抛物线C经过点B,求其解析式;
(3)设抛物线C交 轴于点M,若△APM为直角三角形,∠APM为直角,求点M的坐标。
轴于点M,若△APM为直角三角形,∠APM为直角,求点M的坐标。