2008-2009学年度聊城市阳谷第二学期九年级期中水平检测与反馈
数学试卷
第I卷 (选择题共26分)
一、选择题(本题共12个小题,每小题3分,共36分,)
1.将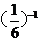 ,(一2)0,(一3)2这三个数按从小到大的顺序排列,正确的结果是( )
,(一2)0,(一3)2这三个数按从小到大的顺序排列,正确的结果是( )
A.(一2)0<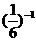 <(-3)2 B.
<(-3)2 B.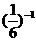 <(-2)0<(一3)2
<(-2)0<(一3)2
C.(-3)2<(一2)0 <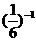 D.(-2)0<(-3)2<
D.(-2)0<(-3)2<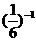
2.下列二次根式中,与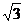 是同类二次根式的是( )
是同类二次根式的是( )
A. B.
B.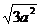 C.
C.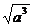 D.
D.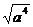
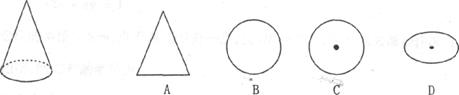
3.如图所示的圆锥的俯视图为( )
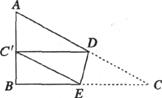
4.如图在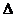 ABC中,∠B=90°,AB=6,BC=8,将
ABC中,∠B=90°,AB=6,BC=8,将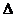 ABC沿DE折叠,使点C落在AB边上的C’处,并且C’D∥BC,则CD的长为( )
ABC沿DE折叠,使点C落在AB边上的C’处,并且C’D∥BC,则CD的长为( )
A.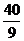 B.
B.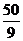 C.
C.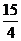 D.
D.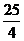
5.某课外兴趣小组为了解所在地区老年人的健康状况,分别作了几种不同的抽样调查,你认为抽样比较合理的是( )
A.在公园调查了1000名老年人的健康状况
B.在医院调查了1000名老人的键康状况
C.调查了l0名老年邻居的健康状况
D.利用派出所的户口网随机调查了该地区10%的老年人的健康状况
6.若不等式组 的正整数解只有2,则a的整数值为( )
的正整数解只有2,则a的整数值为( )
A.8、9、10 B.9、10、
7.小明同学将某班级毕业升学体育测试成绩(满分30分)统计整理,得到下表,则下列说法错误的是( )
分数
20
21
22
23
24
25
26
27
28
人数
2
4
3
8
10
9
6
3
l
A.该组数据的众数是24分 B.该组数据的平均数是25分
C.该组数据的中位数是24分 D.该组数据的极差是8分
8.如图,身高为
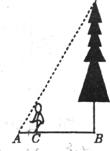
A.
9.如图:既是轴对称图形,又是中心对称图形的是( )

10.有两名男生和两名女生,王老师要随机地两两一对给他们排座位,一男一女排在一起的概率是( )
A.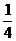 B.
B. C.
C.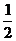 D.
D.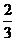
11.随着微电子制造技术的不断进步,半导体材料的精神加工尺寸大幅缩小,目前已经能够在350平方毫米的蕊片上集成5亿个元件,用科学记数法表示1个这样的元件占( )
A.7×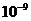 平方毫米 B.7×
平方毫米 B.7×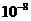 平方毫米
平方毫米
C.7×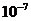 平方毫米 D.7×
平方毫米 D.7×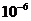 平方毫米
平方毫米
12.为确保信息安全,信息需要加密传输,发送方由明文→密文(加密) →接收方由密文→明文(解密)。已知加密规则为:明文a,b,c对应的密文a+1,2b+4。
A.4、5、6 B.6、7、
第Ⅱ卷 (非选择题 共84分)
二、填空题(本题共5个小题?每小题3分。共l5分。只要求填写最后结果)
13.计算:(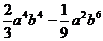 )÷
)÷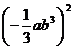 =________________________________
=________________________________
14.方程组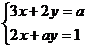 中的x与y互为相反数,则a=________________________
中的x与y互为相反数,则a=________________________
15.⊙O的半径为5┩,点P是⊙O外一点,且OP=
16.多项式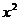 ―6x+2k一1分解因式后写成(
―6x+2k一1分解因式后写成(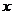 +m)2的形式,则k的值为_________。
+m)2的形式,则k的值为_________。
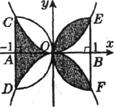
17.如图:半圆A与半圆B均与y轴相切与点O,其直径CD、EF均和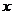 轴垂直,以O为顶点的两条抛物线分别经过点C、E和点D、F,则图中阴影部分的面积为:_______________.
轴垂直,以O为顶点的两条抛物线分别经过点C、E和点D、F,则图中阴影部分的面积为:_______________.

三、解答题(本题共8个小题,共69分。解答应写出文字说明。证明过程或推演步骤)
18.(本题满分6分)先化简再求值:
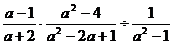 ,其中
,其中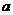 满足
满足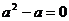
19.(本题满分7分)学习了统计知识后,明明就本班同学的上学方式进行了一次调查统计.图1和图2是他通过收集数据并整理后绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
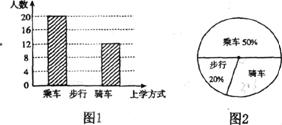
(1)该班共有学生多少名?
(2)在图1中,将表示“步行”的部分补完整;
(3)在扇形统计图中,计算“骑车”部分所对应的圆心角的度数;
(4)如果全年级共500名同学,请你估算全年级步行上学的学生人数。
20.(本题满分8分)如图,EG∥AF,请你从下面三个条件中,再选两个作已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况)
①AB=AC ②DE=DF ③BE=CF
已知:EG∥AF,____________=________________,_____________=_______________。
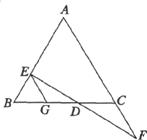
求证:
证明:
21.(本题满分9分)项王故里的门票价格规定如下表:
购票人数
每人门票价
1―50人
5元
51一l00人
4.5元
100人以上
4元
某校九年级甲、乙两个班共有103人(其中甲班人数多于乙班人数)去游项王故里,如果两班都以班为单位分别购票,则一共需486元.
(1)如两班联合起来作为一个团体购票,则可以节约多少元钱?
(2)两班各有多少名学生?
22.(本题满分7分)如图,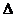 ABC内接于⊙O,过C作CD∥AB与⊙O相交于D点,E是
ABC内接于⊙O,过C作CD∥AB与⊙O相交于D点,E是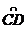 上一点,且满足AD=DE连接BD与AE相交于点F
上一点,且满足AD=DE连接BD与AE相交于点F
求证:△ADF∽△ABC
23.(本题满分l3分)抛物线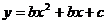 与
与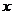 轴交于A(一1,0)、B(3,0)两点。
轴交于A(一1,0)、B(3,0)两点。
(1)求该抛物线的解析式:
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足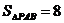 ,并求出此时P点的坐标;
,并求出此时P点的坐标;
(3)设(1)中的抛物线交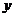 轴于C点,在该抛物线的对称轴上是否存在点Q,使得
轴于C点,在该抛物线的对称轴上是否存在点Q,使得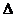 QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

24.(本题满8分)将正六边形纸片按下列要求分割(每次分割,纸片均不得有剩余);
第一次分割:将正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形再分割成一个正六边形和两个全等的正三角形;
第二次分割:将第一次分割后所得的正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形再分割成一个正六边形和两个全等的正三角形;按上述分割方法进行下去……
(1)请你在下图中画出第一次分割的示意图;
(2)若原正六边形的面积为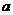 ,请你通过操作和观察,将第l次,第2次,第3次分割后所得的正六边形的面积填入下表:
,请你通过操作和观察,将第l次,第2次,第3次分割后所得的正六边形的面积填入下表:
分割次数(n)
1
2
3
…
正六边形的面积s
(3)观察所填表格,并结合操作,请你猜想:分割后所得的正六边形的面积S与分割次数,n有何关系?(s用含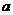 和n的代数式表示,不需要写出推理过程)
和n的代数式表示,不需要写出推理过程)
25.(本题满分l l分)一家化工厂原来每月利润为l20万元.从今年一月起安装使用回收净化设备(安装时间不计),一方面改善了环境,另一方面大大降低原料成本.据测算,使用回收净化设备后的l至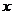 月(1≤
月(1≤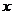 ≤12)的利润的月平均值
≤12)的利润的月平均值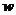 (万元)满足
(万元)满足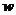 =l0x+90,第2年的月利润稳定在第1年的第l2个月的水平。
=l0x+90,第2年的月利润稳定在第1年的第l2个月的水平。
(1)设使用回收净化设备后的1至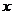 月(1≤
月(1≤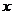 ≤12)的利润和为y,写出
≤12)的利润和为y,写出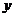 关于
关于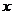 的函数关系式,并求前几个月的利润和等于700万元?
的函数关系式,并求前几个月的利润和等于700万元?
(2)当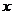 为何值时,使用回收净化设备后的1至
为何值时,使用回收净化设备后的1至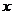 月的利润和与不安装回收净化设备时
月的利润和与不安装回收净化设备时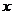 个月的利润和相等?
个月的利润和相等?
(3)求使用回收净化设备后两年的利润总和。