2009年临沂市中考模拟数学试题(四)
说明:本试题满分120分,考试时间120分钟。
第Ⅰ卷(选择题 共42分)
一、选择题(本大题共14小题,每小题3分,共42分。在每小题所给的四个选项中,只有一项是符合题目要求的。)
1. 的绝对值是
的绝对值是
A.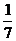 B.
B. C.7 D.-7
C.7 D.-7
2.为支援四川地震灾区,中央电视台于
A.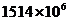 B.
B.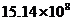 C.
C.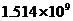 D.
D.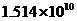
3.下列运算中,结果正确的是
A.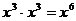 B.
B.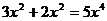
C.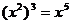 D.
D.
4.如下图,△OAB绕点O逆时针旋转80°到△OCD的位置,已知∠AOB=45°,则∠AOD=

A.55° B.45° C.40° D.35°
5.将不等式组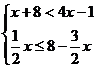 的解集在数轴上表示出来,正确的是
的解集在数轴上表示出来,正确的是

6.已知样本数据1,2,4,3,5,下列说法不正确的是
A.平均数为3 B.中位数为4 C.极差是4 D.方差是2
7.计算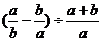 的结果为
的结果为
A.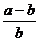 B.
B.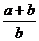 C.
C.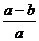 D.
D.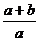
8.小刚身高
A.
9.如下图,阴影部分组成的图案既是关于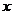 轴成轴对称的图形,又是关于坐标原点O成中心对称的图形,若点A的坐标为(1,3),则点M和点N的坐标分别为
轴成轴对称的图形,又是关于坐标原点O成中心对称的图形,若点A的坐标为(1,3),则点M和点N的坐标分别为
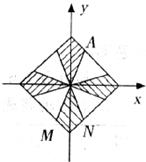
A.M(1,-3) N(-1,-3) B.M(-1,-3) N(-1,3)
C.M(-1,-3) N(1,-3) D.M(-1,3) N(1,-3)
10.已知反比例函数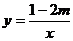 的图像上两点A(
的图像上两点A(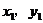 )B(
)B(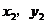 ),当
),当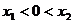 ,
,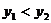 ,则
,则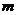 的取值范围是
的取值范围是
A.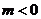 B.
B. C.
C.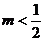 D.
D.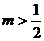
11.如下图所示的正方形花园ACDE中,ABGF是正方形,AB为
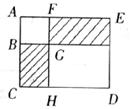
A.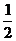 B.
B.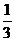 C.
C.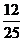 D.
D.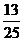
12.如下图所示,有一张一个角为60°的直角三角形纸片,设其中一条中位线剪开后,不能拼成的四边形是
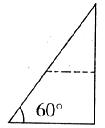
A.邻边不等的矩形 B.等腰梯形
C.有一个角是锐角的菱形 D.正方形
13.如下图,设M、N分别为直角梯形ABCD两腰AD、CB的中点,DE⊥AB于E点,将△ADE沿DE翻折,M与N恰好重合,则AE┱BE等于
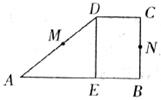
A.2┱1 B.3┱2 C.1┱2 D.2┱3
14.当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解决“燃眉之急”,如下图,已知矩形ABCD,我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片使点B落在AD上,折痕与BC交于E,(2)将纸片展开后,再一次折叠纸片,以点E所在直线为折痕,使点A落在BC上,折痕EF交AD于F,则∠AFE=

A.60° B.67.5° C.72° D.75°
第Ⅱ卷(非选择题 共78分)
二、填空题(本大题共5小题,每小题3分,共15分)
15.分解因式: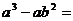 ___________。
___________。
16.方程组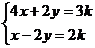 的解
的解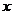 和
和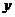 的值相等,则
的值相等,则 的值是___________。
的值是___________。
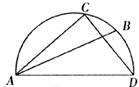
17.如下图所示的半圆中,AD是直径且AD=3,AC=2,则sinB的值是___________。
18.在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD为矩形,你所添加的条件是___________(写出一种情况即可)。

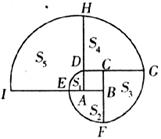
19.如下图:四边形ABCD为正方形,曲线DEFGHI……叫“正方形ABCD的渐开线”,其中 ……的圆心依次是A、B、C、D循环,当渐开线延伸开时,形成了扇形
……的圆心依次是A、B、C、D循环,当渐开线延伸开时,形成了扇形 ……,当AB=1时,它们的面积
……,当AB=1时,它们的面积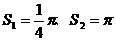 、
、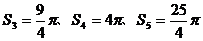 ……,那么扇形
……,那么扇形 的面积是___________。
的面积是___________。
三、开动脑筋,你一定能做对!(本大题共3小题,共20分)
20.(本小题满分6分)
某厂生产一种产品,下面左图是该厂第一季度三个月产量的统计图,右图是这三个月的产量与第一季度总产量的比例分布统计图。统计图员在制作左图、右图时漏填了部分数据。
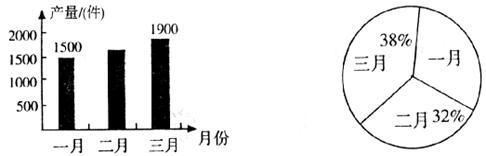
根据上述信息,回答下列问题:
(1)该厂第一季度哪个月的产量最高?__________月;
(2)该厂一月份产量占第一季度产量的__________%;
(3)该厂质检科从第一季度的产品中随机抽样;抽检结果发现样品的合格率为98%,请你估计,该厂第一季度大约生产了多少件合格的产品?(写出解题过程)
21.(本小题满分7分)
如下图,已知A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD。
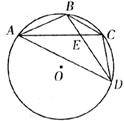
(1)求证:DB平分∠ADC。
(2)若BE=3,ED=6,求AB的长。
22.(本小题满分7分)
为了解决农民工子女入学难的问题,某市建立了一套进城农民工子女就学的保障机制,其中一项就是免交“借读费”,据统计2004年秋就有5000名农民工子女进入主城区中小学学习,到2005年秋季进入主城区中小学学习的农民工子女比2004年有所增加。其中小学增加了20%,中学增加了30%,这样2005年秋季新增了1160名农民工子女在主城区中小学学习。
(1)如果按小学每生每年收“借读费”500元,中学每生收“借读费”1000元计算,求2005 年新增的1160名中小学生,共免收多少“借读费”?
(2)如果小学每40名学生配备2名教师,中学每40名学生配备3名教师,若按2005年秋季入学后,农民工子女在主城区中小学就读的学生人数计算,一共需要配多少名教师?
四、认真思考,你一定能成功!(本大题共2小题,共19分)
23.(本小题满分9分)
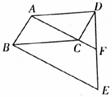
如下图,ABCD为平行四边形,AD=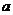 ,BE∥AC,DE交AC的延长线于F点,交BE于E 点。
,BE∥AC,DE交AC的延长线于F点,交BE于E 点。
(1)求证:DF=FE;
(2)若AC=2CF,∠ADC=60°,AC⊥DC,求BE的长;
(3)在(2)的条件下,求四边形ABED的面积。
24.(本小题满分10分)
某果园有100棵桃树,现准备多种一些桃树,以提高产量,增加收入,经过试验调查得到每增种10棵桃树,每棵桃树少结20个桃子,已知每个桃子0.5元,现有下表有关数据:
增种桃树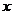 (棵)
(棵)
10
20
30
’
40
桃树产量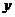 (个/棵)
(个/棵)
340
桃子总产量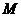 (个)
(个)
43200
44800
总收入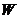 (元)
(元)
20900
21600
(1)根据题意和表中已有的数据,在表中空白处填上适当的数;
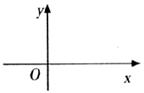
(2)如下图,在平面直角坐标系中,根据(1)中数据描出实数对(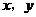 )的对应点,根据你的描点,猜想
)的对应点,根据你的描点,猜想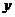 与
与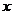 的函数关系式;
的函数关系式;
(3)根据(2)中的关系式,求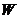 与
与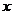 的函数关系式,并求增种多少棵桃树,可获得最大收入为多少元?
的函数关系式,并求增种多少棵桃树,可获得最大收入为多少元?
五、相信自己,加油呀!(本大题共2小题,共24分)
25.(本小题满分12分)
在正方形ABCD中,点P是CD上一动点,连接PA,分别过点B、D作BE⊥PA,DF⊥PA,垂足为E、F(如图①)。
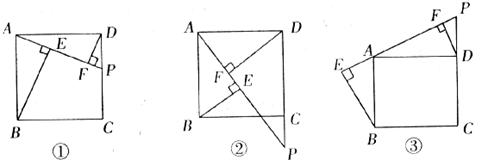
(1)请探索BE、DF、EF这三条线段的长度具有怎样的数量关系,若点P在DC的延长上(如图②),那么这三条线段的长度之间又有怎样的数量关系?若点P在CD的延长线上呢(如图③)?请分别直接写出结论。
(2)请在(1)中的三个结论中选择一个加以证明。
26.(本小题满分12分)
已知:如下图,在平面直角坐标系中,四边形ABCD是菱形,且∠AOC=60°,点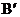 的坐标是(0,
的坐标是(0,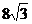 ),点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动,同时点Q 开始以每秒
),点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动,同时点Q 开始以每秒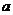 (
(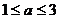 )个单位长度的速度沿射线OA方向移动,设
)个单位长度的速度沿射线OA方向移动,设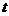 (
(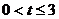 )秒后,直线DQ交OB于点D。
)秒后,直线DQ交OB于点D。
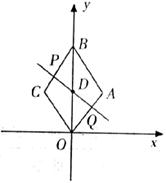
(1)求∠AOB的度数及线段似的长;
(2)求经过A、B、C三点的抛物线的解析式;
(3)当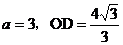 时,求
时,求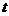 的值及此时直线PQ的解析式;
的值及此时直线PQ的解析式;
(4)当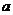 为何值时,以O、Q、D为顶点的三角形与△OAB相似?当
为何值时,以O、Q、D为顶点的三角形与△OAB相似?当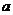 为何值时,以O、Q、D为顶点的三角形与△OAB不相似?请给出你的结论,并加以证明。
为何值时,以O、Q、D为顶点的三角形与△OAB不相似?请给出你的结论,并加以证明。