2009年四川省遂宁市初中毕业生学业考试
数学试卷
说明:1.本试卷分第Ⅰ卷和第Ⅱ卷.第Ⅰ卷1―2页为选择题,第Ⅱ卷3―8页为非选择题.请将第Ⅰ卷的正确选项填在第Ⅱ卷前面的第Ⅰ卷答题表内;第Ⅱ卷用蓝、黑色的钢笔或圆珠笔直接解答在试卷上,其中的解答题都应按要求写出必要的解答过程.
2.本试卷满分150分,答题时间为120分钟.
第Ⅰ卷(选择题,共36分)
一、选择题(本大题共12个小题,每小题3分,共36分)
1.5的相反数是
A.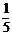 B.
B.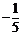
2.做重复实验:抛掷同一枚啤酒瓶盖1000次.经过统计得“凸面向上”的频率约为0.44,则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为
A.0.22
B.
3.下列计算正确的是
A.2x+x=x3
B.(3x)2=6x
4.如图,已知∠1=∠2,∠3=80O,则∠4=

A.80O B.70O C.60O D.50O
5.数据0.000207用科学记数法表示为
A.2.07×10-3 B.2.07×10
6.如图,已知⊙O的两条弦AC,BD相交于点E,∠A=70o,∠c=50o,那么sin∠AEB的值为
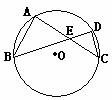
A.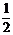 B.
B.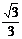 C.
C.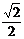 D.
D.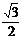
7.把二次函数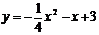 用配方法化成
用配方法化成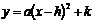 的形式
的形式
A.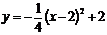 B.
B.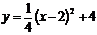
C.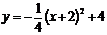 D.
D.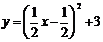
8.一个正方体的表面展开图如图所示,每个面内都标注了字母,如果从正方体的右面看是面D,面C在后面,则正方体的上面是
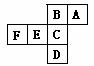
A.面E B.面F C.面A D.面B
9.一组数据2,3,2,3,5的方差是
A.6
B.
10.如图,把⊙O1向右平移8个单位长度得⊙O2,两圆相交于A、B,且O
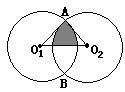
A.4π-8
B.8π
11.如图,在梯形ABCD中,AB//DC,∠D=90o,AD=DC=4,AB=1,F为AD的中点,则点F到BC的距离是
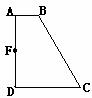
A.2
B.
12.已知整数x满足-5≤x≤5,y1=x+1,y2=-2x+4,对任意一个x,m都取y1,y2中的较小值,则m的最大值是
A.1
B.
二、填空题(本大题共5个小题,每小题4分,共20分)把答案直接填在题目中的横线上.
13.把不等式组的解集表示在数轴上,如图所示,那么这个不等式组的解集是 .

14.分解因式:x3-4x= .
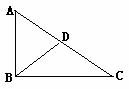
15.如图,已知△ABC中,AB=
16.把只有颜色不同的1个红球和2个白球装入一个不透明的口袋里搅匀,从中随机地一次摸出2个球,得1红球1白球的概率为 .
17.已知△ABC中,AB=BC≠AC,作与△ABC只有一条公共边,且与△ABC全等的三角形,这样的三角形一共能作出 个.
三、解答题(本大题共4个小题,每小题10分,共40分)
18.计算: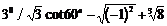
19.某校初三年级共有学生540人,张老师对该年级学生的升学志愿进行了一次抽样调查,他对随机抽取的一个样本进行了数据整理,绘制了两幅不完整的统计图(图甲和图乙)如下.请根据图中提供的信息解答下列问题:
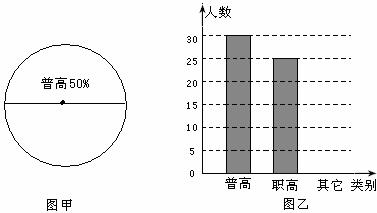
⑴求
⑵把图甲和图乙都补充绘制完整;
⑶请估计全年级填报就读职高的学生人数.
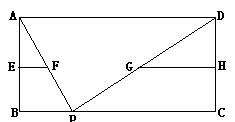
20.如图,已知矩形ABCD中,AB=
⑴求证:EF+GH=
⑵求当∠APD=90o时,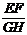 的值.
的值.
21.在A、B两个盒子中都装着分别写有1~4的4张卡片,小明分别从A、B两个盒子中各取出一张卡片,并用A盒中卡片上的数字作为十位数,B盒中的卡片上的数字作为个位数.请画出树状图,求小明抽取一次所得两位数能被3整除的概率.
四、解答题(本大题共2小题,每小题12分,共24分)
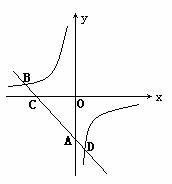
22.如图,已知直线y=ax+b经过点A(0,-3),与x轴交于点C,且与双曲线相交于点B(-4,-a).
⑴求直线和双曲线的函数关系式;
⑵求△CDO(其中O为原点)的面积.
23.某校原有600张旧课桌急需维修,经过A、B、C三个工程队的竞标得知,A、B的工作效率相同,且都为C队的2倍,若由一个工程队单独完成,C队比A 队要多用10天.学校决定由三个工程队一齐施工,要求至多6天完成维修任务.三个工程队都按原来的工作效率施工2天时,学校又清理出需要维修的课桌360张,为了不超过6天时限,工程队决定从第3天开始,各自都提高工作效率,A、B队提高的工作效率仍然都是C队提高的2倍.这样他们至少还需要3天才能成整个维修任务.
⑴求工程队A原来平均每天维修课桌的张数;
⑵求工程队A提高工作效率后平均每天多维修课桌张数的取值范围.
五、解答题(本大题2小题,每小题15分,共30分)
24.如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF?AC,cos∠ABD=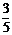 ,AD=12.
,AD=12.
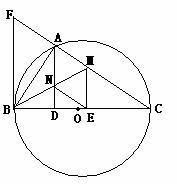
⑴求证:△ANM≌△ENM;
⑵求证:FB是⊙O的切线;
⑶证明四边形AMEN是菱形,并求该菱形的面积S.
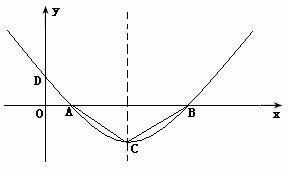
25.如图,二次函数的图象经过点D(0,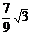 ),且顶点C的横坐标为4,该图象在x 轴上截得的线段AB的长为6.
),且顶点C的横坐标为4,该图象在x 轴上截得的线段AB的长为6.
⑴求二次函数的解析式;
⑵在该抛物线的对称轴上找一点P,使PA+PD最小,求出点P的坐标;
⑶在抛物线上是否存在点Q,使△QAB与△ABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由.