2009年北京市密云县初三综合检测(一)
![]()
数学试卷
第I卷(机读卷 共32分)
一、选择题(共8个小题,每小题4分,共32分)
1.2的倒数是( )
A.-2 B.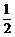 D.
D.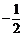
2.长城总长约为
A.6.7×
3.函数 的自变量
的自变量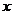 的取值范围是( )
的取值范围是( )
A.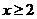 B.
B.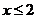 C.
C. 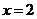 D.
D.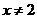
4.城子中学的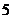 位同学在“汶川地震”捐款活动中,捐款如下(单位:元):
位同学在“汶川地震”捐款活动中,捐款如下(单位:元):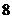 ,
, ,
,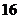 ,
,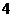 ,
,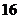 那么这组数据的众数、中位数、平均数分别为( )
那么这组数据的众数、中位数、平均数分别为( )
A.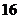 ,
,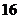 ,
,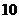 B.
B.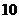 ,
,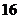 ,
,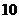
C.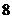 ,
,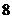 ,
,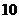 D.
D.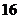 ,
,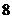 ,
,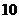
5.若一个多边形的内角和等于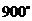 ,则这个多边形的边数是(
)
,则这个多边形的边数是(
)
A.5 B.
6.把代数式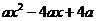 分解因式,下列结果中正确的是( )
分解因式,下列结果中正确的是( )
A.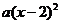
 B.
B.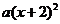
C.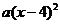 D.
D.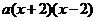
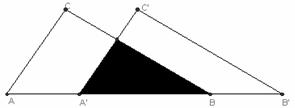
7.如下图,把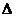 ABC沿AB边平移到
ABC沿AB边平移到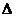 A’B’C’的位置,它们的重叠部分(即图中阴影部分)的面积是
A’B’C’的位置,它们的重叠部分(即图中阴影部分)的面积是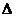 ABC面积的一半,若AB=
ABC面积的一半,若AB=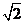 ,则此三角形移动的距离AA’是( )
,则此三角形移动的距离AA’是( )
A.
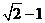 B.
B.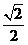 C.1
D.
C.1
D.
8.如下图,已知MN是圆柱底面的直径,NP是圆柱的高,在圆柱的侧面上,过点M、P嵌有一圈路径最短的金属丝,现将圆柱侧面沿NP剪开,所得的侧面展开图是( )
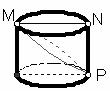

A B C D
第Ⅱ卷(88分)
二、填空题:(本大题共4个小题,每小题4分,共16分)把答案直接填写在题中横线上.
9.若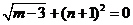 ,则
,则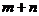 的值为 .
的值为 .
10.若关于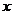 的一元二次方程
的一元二次方程
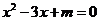 有实数根,则
有实数根,则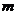 的取值范围是 .
的取值范围是 .
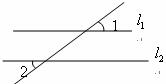
11.如下图,已知直线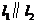 ,
,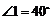 ,那么
,那么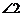
 .
.
12.已知,⊙O的半径为3cm, ⊙O的切线长AB为6cm,B为切点.则点A到圆上的最短距离是 cm,最长距离是 cm.
三、解答题(共5个小题,每小题5分,共25分)
13.(本小题满分5分)
求值:-22 + tan 60o -(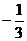 )-1+
)-1+
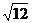 .
.
14.(本小题满分5分)
先化简,再求值:
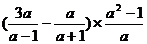 ,其中a=
,其中a=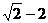
15.(本小题满分5分)
解不等式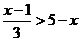 ,并把解集表示在数轴上.
,并把解集表示在数轴上.
16.(本小题满分5分)
已知:如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F,
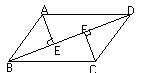
求证:∠BAE=∠DCF.
17.(本小题满分5分)
服装厂准备加工300套演出服.在加工60套后,采用了新技术,使每天的工作效率是原来的2倍,结果共用9天完成任务.求该厂原来每天加工多少套演出服.
四、解答题(共2个小题,每小题5分,共10分)
18.(本小题满分5分)
在平面直角坐标xoy系中,直线y= -x关于y轴的对称直线l与反比例函数 的图象的一个交点为A(a,3),试确定反比例函数的解析式.
的图象的一个交点为A(a,3),试确定反比例函数的解析式.
19.(本小题满分5分)
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,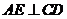 于E,DA平分
于E,DA平分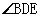 .
.
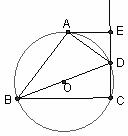
(1)求证:AE是⊙O的切线;
(2)若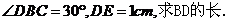
五、 解答题(共2个小题,每小题5分,共10分)
20.(本小题满分5分)
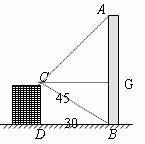
北京市在城市建设中,要拆除旧烟囱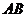 (如图所示),在烟囱正西方向的楼
(如图所示),在烟囱正西方向的楼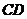 的顶端
的顶端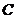 ,测得烟囱的顶端
,测得烟囱的顶端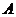 的仰角为
的仰角为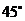 ,底端
,底端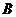 的俯角为
的俯角为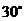 ,已量得
,已量得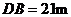 .拆除时若让烟囱向正东倒下,试问:距离烟囱东方
.拆除时若让烟囱向正东倒下,试问:距离烟囱东方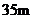 远的一棵大树是否被歪倒的烟囱砸着?请说明理由.(
远的一棵大树是否被歪倒的烟囱砸着?请说明理由.(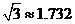 )
)
21.(本小题满分5分)
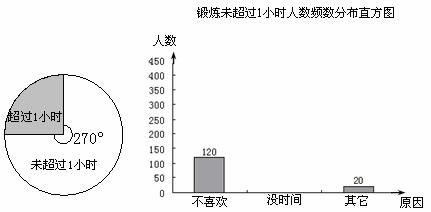
国家教委规定“中小学生每天在校体育活动时间不低于1小时”.为此,某地区今年初中毕业生学业考试体育学科分值提高到40分,成绩记入考试总分.某中学为了了解学生体育活动情况,随机调查了720名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”,所得的数据制成了的扇形统计图和频数分布直方图.
根据图示,解答下列问题:
(1)若在被调查的学生中随机选出一名学生测试其体育成绩,选出的恰好是“每天锻炼 超过1小时”的学生的概率是多少?
(2)“没时间”的人数是多少?并补全频数分布直方图;
(3)2008年这个地区初中毕业生约为4.3万人,按此调查,可以估计2008年这个地区初中毕业生中每天锻炼未超过1小时的学生约有多少万人?
(4)请根据以上结论谈谈你的看法.
六、解答题
22.(本小题满分5分)
如下图所示,直线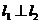 ,垂足为点
,垂足为点 ,A、B是直线
,A、B是直线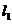 上的两点,且OB=2,AB=
上的两点,且OB=2,AB=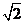 ,直线
,直线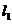 绕点O按逆时针方向旋转,旋转角度为
绕点O按逆时针方向旋转,旋转角度为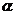
 。
。
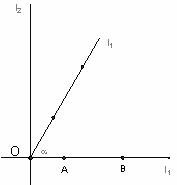
(1)当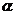 =60
=60 时,在直线
时,在直线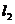 上找点P,使得
上找点P,使得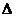 BPA是以
BPA是以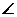 B为顶角的等腰三角形,此时OP= ;
B为顶角的等腰三角形,此时OP= ;
(2)当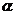 在什么范围内变化时,直线
在什么范围内变化时,直线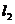 上存在点P,使得
上存在点P,使得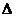 BPA是以
BPA是以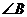 为顶角的等腰三角形,请用不等式表示
为顶角的等腰三角形,请用不等式表示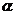 的取值范围:
.
的取值范围:
.
七、解答题(本题满分7分)
23.关于x的方程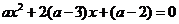 至少有一个整数解,且a是整数,求a的值.
至少有一个整数解,且a是整数,求a的值.
八、解答题(本题满分7分)
24.已知抛物线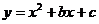 经过点A(0,5)和B(3,2)点.
经过点A(0,5)和B(3,2)点.
(1)求抛物线的解析式;
(2)现有一半径为1,圆心P在抛物线上运动的动圆,问当⊙P在运动过程中,是否存在⊙P与坐标轴相切的情况?若存在,请求出圆心P的坐标;若不存在,请说明理由;
(3)若⊙Q的半径为r,点Q在抛物线上,当⊙Q与两坐标轴都相切时,求半径r的值.
九、解答题(本题满分8分)
25.已知等边三角形ABC中,点D、E、F分别为AB、AC、BC边的中点,M为直线BC上一动点,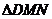 为等边三角形(点M的位置改变时,
为等边三角形(点M的位置改变时,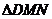 也随之整体移动).
也随之整体移动).
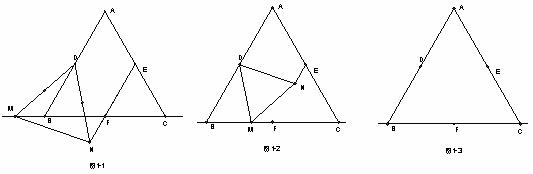
(1)如图1-1,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?请直接写出结论,不必证明或说明理由;
(2)如图1-2,当点M在BC边上,其它条件不变时,(1)的结论中EN与MF的数量关系是否依然成立?若成立,请利用图1-2证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图1-3中作出相应的图形(不写作法),(1)结论中EN与MF的数 量关系是否仍然成立?请直接写出结论,不必证明或说明理由.