2009年四川省泸州市初中毕业考试暨高中阶段学校招生统一考试
数学试卷
(考试时间:只完成A卷90分钟,完成A、B卷120分钟)
说明:
1.本次考试试卷分为A、B卷,只参加毕业考试的考生只需完成A卷,要参加升学考试的学生必须加试B卷。
2.A卷分为第I 卷和第Ⅱ卷两部分,第I卷为选择题,第Ⅱ卷为非选择题,满分100分;B卷为非选择题,满分50分。A、B卷满分共150分。
3.本卷中非选择题部分的试题,除题中设计有横线的题目外,解答过程都必须有必要的文字说明、演算步骤或推理证明。
A卷
第I卷 选择题(共30分)
注意事项:
1.第Ⅰ卷共2页,答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目填写在答题卡上。考试结束后,监考人员将试卷和答题卡一并收回。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦擦干净后再选涂其它答案。不能答在试卷上。
一、选择题(本大题10个小题,共30分,每小题3分)在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在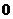 ,
,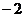 ,
,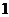 ,
,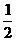 这四个数中,最小的数是
这四个数中,最小的数是
A.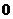 B.
B.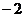 C.1 D.
C.1 D.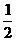
2.化简: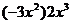 的结果是
的结果是
A.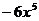 B.
B.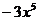 C.
C.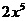 D.
D.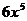
3.如图,P是正△ABC内的一点,若将△PBC绕点B旋转到△P’BA,则∠PBP’的度数是
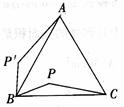
A.45° B.60° C.90° D.120°
4.在一次青年歌手大奖赛上,七位评委为某位歌手打出的分数如下:9.5, 9.4, 9.6, 9.9, 9.3, 9.7,9.0,去掉一个最高分和一个最低分后,所剩数据的平均数是
A.9.2 B.
5.已知⊙O1与⊙O2的半径分别为
A.外离 B.外切 C.相交 D.内切
6.不等式组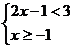 的解集是
的解集是
A.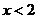 B.
B.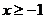 C.
C.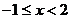 D.无解
D.无解
7.已知反比例函数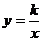 的图象经过点P(一l,2),则这个函数的图象位于
的图象经过点P(一l,2),则这个函数的图象位于
A.第二、三象限 B.第一、三象限
C.第三、四象限 D.第二、四象限
8.如图,是一个物体的俯视图,它所对应的物体是

9.在平面直角坐标系中,将二次函数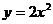 的图象向上平移2个单位,所得图象的解析式为
的图象向上平移2个单位,所得图象的解析式为
A.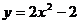 B.
B.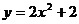
C.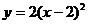 D.
D.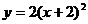
10.将棱长是lcm的小正方体组成如图所示的几何体,那么这个几何体的表面积是
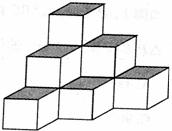
A.
第Ⅱ卷(非选择题 共70分)
注意事项:
1.第Ⅱ卷共4页,用钢笔或圆珠笔直接答在试卷上。
2.答卷前将密封线内的项目填写清楚。
二、填空题(本大题4个小题,共16分,每小题4分)把答案填在题中的横线上.
11.分解因式: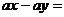
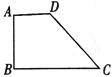
12.如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=3,BC=4,则梯形ABCD的面积是
13.关于x的方程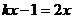 的解为正实数,则k的取值范围是
的解为正实数,则k的取值范围是
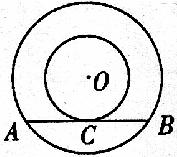
14.如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为
三、(本大题2个小题,共16分,每小题8分)
15.计算: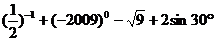
16.化简: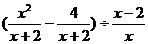 )
)
四、(本大题2个小题,共18分,每小题9分)
17.某校为了了解九年级学生体育测试成绩情况,抽查了一部分学生的体育测试成绩,甲、乙、丙三位同学将抽查出的学生的测试成绩按A、B、C、D四个等级进行统计,并将统计结果绘制成如下统计图,其中测试成绩在90~100分为A级,75~89分为B级, 60~74分为C级,60分以下为D级。甲同学计算出成绩为C的频率是0.2,乙同学计算出成绩为A、B、C的频率之和为0.96,丙同学计算出成绩为A的频数与成绩为B的频数之比为7:12.结合统计图回答下列问题:

(1)这次抽查了多少人?
(2)所抽查学生体育测试成绩的中位数在哪个等级内?
(3)若该校九年级学生共有500人,请你估计这次体育测试成绩为A级和B级的学生共有多少人?
18.如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
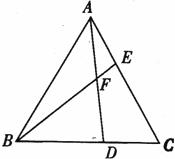
(1)求证: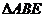 ≌△CAD;
≌△CAD;
(2)求∠BFD的度数.
五.(本题满分10分)
19.已知一次函数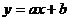 的图象经过点A(
的图象经过点A(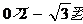 ,B(
,B(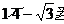 ,C(
,C(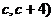 .
.
(1)求c;
(2)求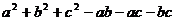 的值.
的值.
六、(本题满分10分)
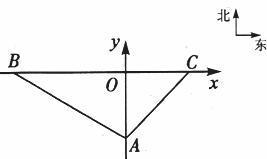
20.在某段限速公路BC上(公路视为直线),交通管理部门规定汽车的最高行驶速度不能超过60千米/时(即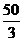 米/秒),并在离该公路
米/秒),并在离该公路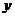 轴上,测速路段BC在
轴上,测速路段BC在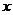 轴上,点B在A的北偏西60°方向上,点C在A的北偏东45°方向上,另外一条高等级公路在
轴上,点B在A的北偏西60°方向上,点C在A的北偏东45°方向上,另外一条高等级公路在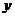 轴上,AO为其中的一段.
轴上,AO为其中的一段.
(1)求点B和点C的坐标;
(2)一辆汽车从点B匀速行驶到点C所用的时间是15秒,通过计算,判断该汽车在这段限速路上是否超速?(参考数据: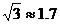 )
)
(3)若一辆大货车在限速路上由C处向西行驶,一辆小汽车在高等级公路上由A处向北行驶,设两车同时开出且小汽车的速度是大货车速度的2倍,求两车在匀速行驶过程中的最近距离是多少?
B 卷
一、填空题:本大题共5个小题,每小题4分,共20分.把答案填在题中的横线上.
1.计算: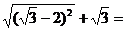
2.某商店一套服装的进价为200元,若按标价的80%销售可获利72元,则该服装的标价为 元.
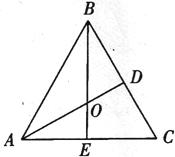
3.如图,在边长为1的等边△ABC中,中线AD与中线BE相交于点O,则OA长度为 .
4.已知方程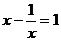 的两根为
的两根为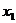 、
、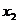 ,则
,则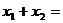 .
.
5.如图,已知Rt△ABC中,AC=3,BC= 4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A ,…,则CA1=
,
,…,则CA1=
,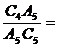

二、解答题:(本大题共3题,共30分)解答题应写出文字说明,证明过程或演算步骤.
6.(本题满分8分)
有A、B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字0,1,2,3, B布袋中有三个除标号外完全相同的小球,小球上分别标有数字0,1,2.小明先从A布袋中随机取出―个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.
(1)若用(m,n)表示小明取球时m与n 的对应值,请画出树状图并写出(m,n)的所有取值;
(2)求关于x的一元二次方程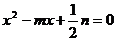 有实数根的概率.
有实数根的概率.
7.(本题满分10分)
如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC,交AB的延长线于E,垂足为F.
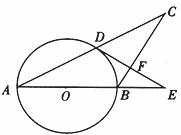
(1)求证:直线DE是⊙O的切线;
(2)当AB=5,AC=8时,求cosE的值.
8.(本题满分12分)
如图,已知二次函数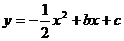
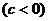 的图象与x轴的正半轴相交于点A、B,与y轴相交于点C,且
的图象与x轴的正半轴相交于点A、B,与y轴相交于点C,且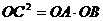 .
.
(1)求c的值;
(2)若△ABC的面积为3,求该二次函数的解析式;
(3)设D是(2)中所确定的二次函数图象的顶点,试问在直线AC上是否存在一点P使△PBD的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
