2009年北京市丰台区一摸练习
数学试卷
第Ⅰ卷 (机读卷 共32分)
一、选择题(共8道小题,每小题4分,共32分)
1.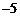 的相反数是
的相反数是
A.5
B.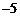 C.
C. D.
D.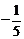
2.在第十一届全国人民代表大会第二次会议上,温家宝总理在政府报告中指出:2008年我国粮食连续五年增产,总产量为52850万吨,创历史最高水平.将52850用科学记数法表示应为
A. B.
B.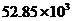 C.
C.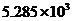 D.
D.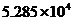
3.五边形的内角和是
A.180° B.360° C.540° D.720°
4.我国部分城市五月某一天最高温度如下表,这些数据的众数和中位数分别是
城市
北京
上海
重庆
杭州
苏州
广州
武汉
最高温度
(℃)
26
25
31
29
29
31
31
A.29,28 B.31,
5.若两圆的半径分别是
A.外离 B.相交 C.外切 D.内切
6.如图,有4张形状、大小、质地均相同的卡片,正面分别写有一个实数,背面完全相同.现将这4张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出卡片正面的实数是无理数的概率是

A. B. C. D.1
7.已知: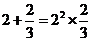 ,
,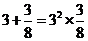 ,
,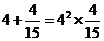 ,
,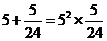 ,…,若
,…,若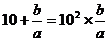 符合前面式子的规律,则
符合前面式子的规律,则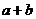 的值为
的值为
A.179
B.
8.将一正方体纸盒沿下下图所示的粗实线剪开,展开成平面图,其展开图的形状为( ).
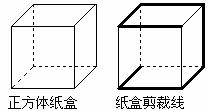

A B C D
第Ⅱ卷 (非机读卷 共88分)
二、填空题(共4道小题,每小题4分,共16分)
9.在函数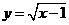 中,自变量
中,自变量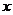 的取值范围是______________.
的取值范围是______________.
10.如图,点A、B、C是⊙O上三点,∠C为20°,则∠AOB  的度数为______°.
的度数为______°.
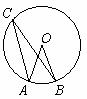
11.分解因式: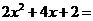 ____________________.
____________________.
12.如图,小正方形方格的边长为
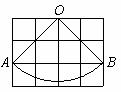
三、解答题(共5道小题,共25分)
13.(本小题满分5分)
计算: .
.
14.(本小题满分5分)
解不等式组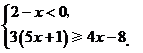
15.(本小题满分5分)
已知:如下图,AB∥DE,∠A=∠D,且BE=CF,
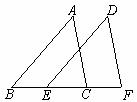
求证:∠ACB=∠F.
16.(本小题满分5分)
先化简,再求值: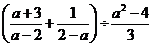 ,其中
,其中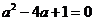 .
.
17.(本小题满分5分)
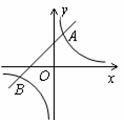
如下图,反比例函数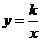 的图象与一次函数
的图象与一次函数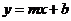 的图象交于
的图象交于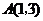 ,
,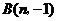 两点.求反比例函数与一次函数的解析式.
两点.求反比例函数与一次函数的解析式.
四、解答题(共2道小题,共10分)
18.(本小题满分5分)
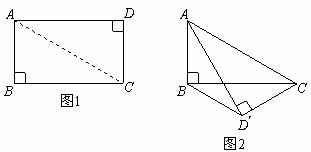
如图1,矩形纸片ABCD中,AB=4,BC=4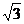 ,将矩形纸片沿对角线AC向下翻折,点D落在点D’处,联结B D’,如图2,求线段BD’ 的长.
,将矩形纸片沿对角线AC向下翻折,点D落在点D’处,联结B D’,如图2,求线段BD’ 的长.
19.(本小题满分5分)
如图,点D是⊙O直径CA的延长线上一点,点B在⊙O上,且AB=AD=AO.
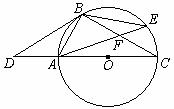
(1)求证:BD是⊙O的切线;
(2)若点E是劣弧BC上一点,弦AE与BC相交于点F,且CF=9,cos∠BFA=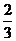 ,求EF的长.
,求EF的长.
五、解答题(本题满分5分)
20.某校学生会准备调查本校初中三年级同学每天(除课间操外)课外锻炼的平均时间.
(1)确定调查方式时,①甲同学说:“我到1班去调查全体同学”;②乙同学说:“我到体育场上去询问参加锻炼的同学”;③丙同学说:“我到初中三年级每个班去随机调查一定数量的同学”.上面同学说的三种调查方式中最为合理的是___________(填写序号);
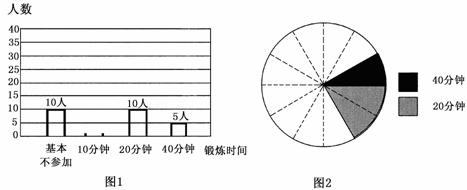
(2)他们采用了最为合理的调查方式收集数据,并绘制出如图1所示的条形统计图和如图2所示的扇形统计图,请将图1补充完整;
(3)若该校初中三年级共有240名同学,则其中每天(除课间操外)课外锻炼平均时间不大于20分钟的人数约为__________人.
(注:图2中相邻两虚线形成的圆心角为30°)
六、解答题(共2道小题,共10分)
21.(本小题满分5分)
列方程或方程组解应用题:
22.(本小题满分5分)
把两个三角形按如图1放置,其中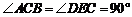 ,
,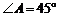 ,
,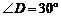 ,且
,且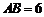 ,
,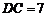 .把△DCE绕点C顺时针旋转15°得到△D1CE1,如图2,这时AB与CD1相交于点
.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图2,这时AB与CD1相交于点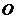 ,与D1E1相交于点F.
,与D1E1相交于点F.
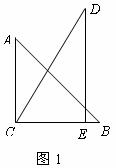
(1)求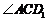 的度数;
的度数;
(2)求线段AD1的长;
(3)若把△D1CE1绕点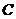 顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.
顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.
七、解答题(本题满分7分)
23.如图1,在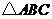 中,
中,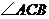 为锐角,点
为锐角,点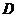 为射线
为射线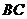 上一点,联结
上一点,联结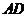 ,以
,以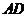 为一边且在
为一边且在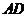 的右侧作正方形
的右侧作正方形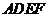 .
.
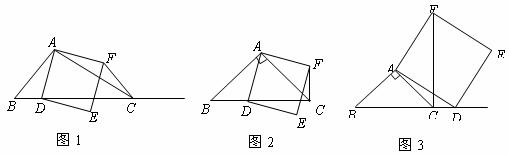
(1)如果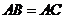 ,
, ,
,
①当点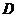 在线段
在线段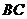 上时(与点
上时(与点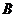 不重合),如图2,线段
不重合),如图2,线段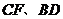 所在直线的位置关系为 __________ ,线段
所在直线的位置关系为 __________ ,线段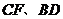 的数量关系为
;
的数量关系为
;
②当点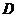 在线段
在线段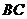 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果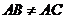 ,
,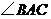 是锐角,点
是锐角,点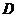 在线段
在线段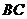 上,当
上,当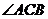 满足什么条件时,
满足什么条件时,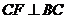 (点
(点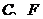 不重合),并说明理由.
不重合),并说明理由.
八、解答题(本题满分7分)
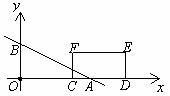
24.如图,在平面直角坐标系中,直线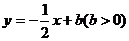 分别交
分别交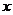 轴、
轴、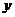 轴于
轴于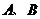 两点.点
两点.点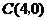 、
、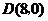 ,以
,以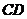 为一边在
为一边在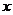 轴上方作矩形
轴上方作矩形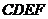 ,且
,且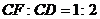 .设矩形
.设矩形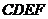 与
与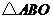 重叠部分的面积为
重叠部分的面积为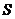 .
.
(1)求点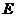 、
、 的坐标;
的坐标;
(2)当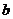 值由小到大变化时,求
值由小到大变化时,求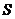 与
与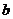 的函数关系式;
的函数关系式;
(3)若在直线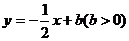 上存在点
上存在点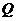 ,使
,使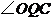 等于
等于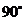 ,请直接写出
,请直接写出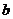 的取值范围.
的取值范围.
九、解答题(本题满分8分)
25.已知抛物线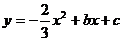 与x轴交于不同的两点
与x轴交于不同的两点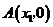 和
和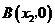 ,与y轴交于点C,且
,与y轴交于点C,且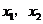 是方程
是方程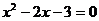 的两个根(
的两个根(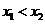 ).
).
(1)求抛物线的解析式;
(2)过点A作AD∥CB交抛物线于点D,求四边形ACBD的面积;
(3)如果P是线段AC上的一个动点(不与点A、C重合),过点P作平行于x轴的直线l交BC于点Q,那么在x轴上是否存在点R,使得△PQR为等腰直角三角形?若存在,求出点R的坐标;若不存在,请说明理由.