2007-2008学年度淮北市九年级“五校”联考(四)
数学试卷
一、选择题(本题共10小题,每小题4分,满分40分)
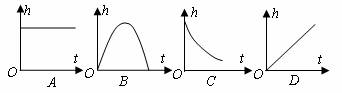
1、足球守门员大脚开出去的球的高度随时间的变化而变化,这一过程可近似地用下列那幅图刻画( )
2、下列四幅图形中,表示两颗小树在同一时刻阳光下的影子的图形可能是( ) 。

A. B. C. D.
3、将叶片图案旋转180°后,得到的图形是( )

4、一物体及其正视图如下图所示,则它的左视图与俯视图分别是右侧图形中的( )
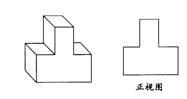
A.①② B.③② C.①④ D.③④
5、二次函数y=ax2+bx+c图象如图所示,则点A(ac,bc)在( ).

A、第一象限 B、第二象限 C、第三象限 D、第四象限
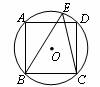
6、如图,正方形ABCD内接于⊙O,点E在劣弧AD上,则∠BEC等于( ).
A、45° B、60° C、30° D、55°
7、在直角坐标系中,⊙O的圆心在圆点,半径为3,⊙A的圆心A的坐标为( ,1),半径为1,那么⊙O与⊙A的位置关系是( )?
,1),半径为1,那么⊙O与⊙A的位置关系是( )?
A. 外离 B.外切 C. 内切 D.相交
8、已知a、b、c为非零实数,且满足 = = = k ,则一次函数y= kx+(1+k)的图象一定经过 …………………………………… ( )
A. 第一、二、三象限 B.第二、四象限 C. 第一象限 D.第二象限
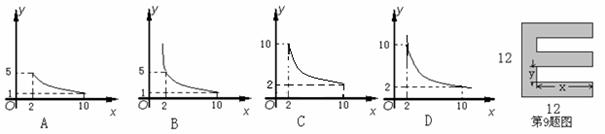
9.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x、y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是……( )
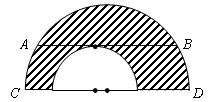
10、如图,两个半圆,大半圆中长为 平行于直径
平行于直径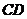 ,且与小半圆相切,则图中阴影部分的面积为( )
,且与小半圆相切,则图中阴影部分的面积为( )
A.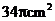 B.
B. C.
C.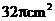 D.
D.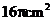
二、填空(本题共4小题,每小题5分,满分20分)
11、在△ABC中, ∠A、∠B、∠C的对边分别是a、b、c,已知∠C=90°, cosB=, a=, 则b= .
12、用反证法证明“四边形的四个内角不能都是锐角”时,应首先假设 .
13、在同一个平面内的两个同心圆,大、小圆的直径分别为
14、已知⊙O的半径是5厘米,在⊙O中有一定点P,且OP=3,那么过点P的弦中,弦长为整数厘米的有_____条。
三、(本题共2小题,每小题8分,满分16分)
15、计算 -
-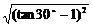 的值
的值
16、不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为.
(1)试求袋中蓝球的个数.
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表格法,求两次摸到都是白球的概率.
四、(本题共2小题,每小题8分,满分16分)
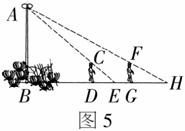
17、如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N.小亮从胜利街的A处,沿着AB方向前进,小明一直站在点P的位置等候小亮.(提醒:本题解答过程可以写在试卷右上角。)

(1)请你在图10中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点C标出);
(2)已知:MN=20 m,MD=8 m,PN=24 m,求(1)中的点C到胜利街口的距离CM.
18、如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=5,BC=3.
(1) 求sin∠BAC的值;
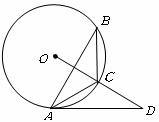
|


 内接于⊙O,点
内接于⊙O,点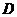 在
在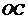 的延长线上,
的延长线上,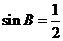 ,
,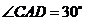 .
.
 是⊙O的切线;
是⊙O的切线; ,
, ,求
,求