2007-2008学年度大兴区第二学期初三模拟检测
数学试卷
第Ⅰ卷 (选择题 共32分)
一、选择题(共8个小题,每小题4分,共32分)
1. ?3的绝对值是( )
A. 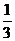 B.
B.
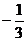 C.
3 D.
C.
3 D.
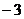
2. 据统计,2006“超级女声”短信投票的总票数约327 000 000张,将这个数写成科学计数法是( )
A.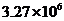 B.
B.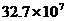 C.
C.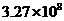 D.
D.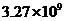
3. 函数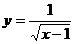 自变量
自变量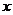 的取值范围是( )
的取值范围是( )
A.x<1
B. x>
4. 下图所示的几何体的俯视图是( ).
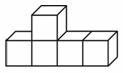
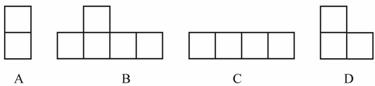
5. 某制衣厂要确定一种衬衫不同号码的生产数量,在做市场调查时,该商家侧重了解的是这种衬衫不同号码的销售数量的( )
A. 平均数 B. 众数
C. 标准差 D. 中位数
6.若关于x的一元二次方程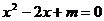 没有实数根,则实数m的取值范围是( ) A.m<l B.m>
没有实数根,则实数m的取值范围是( ) A.m<l B.m>
7.如图,是一次函数y=kx+b与反比例函数y=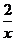 的图象,则关于x的方程kx+b=
的图象,则关于x的方程kx+b=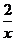 的解为( )
的解为( )

A.xl=1,x2= 2 B.xl= -2,x2= -1
C.xl=1,x2= -2 D.xl=2, x2= -1
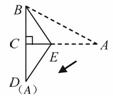
8.如图,在三角形纸片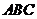 中,
中,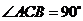 ,
,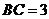 ,
,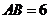 ,在
,在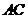 上取一点
上取一点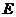 ,以
,以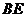 为折痕,使
为折痕,使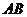 的一部分与
的一部分与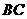 重合,
重合,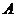 与
与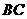 延长线上的点
延长线上的点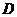 重合,则
重合,则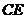 的长度为( )
的长度为( )
A.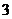 B.
B.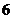 C.
C.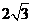 D.
D.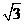
第II卷(非选择题 共88分)
二、填空题(共4个小题,每小题4分,共16分)
9.若反比例函数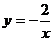 的图象上有两点
的图象上有两点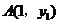 ,
,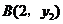 ,则
,则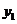 ______
______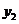 (填“
(填“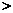 ”或“
”或“ ”或“
”或“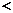 ”).
”).
10.如图,转动转盘,转盘停止转动时指针指向阴影部分的概率是

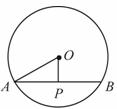
11.如图,⊙O的直径为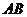 长为
长为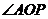 的值为 .
的值为 .
12.自然数按一定规律排成下表,那么第200行的第5个数是 .
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
… … … … …. …. ….. ……….
三、解答题(共5个小题,每小题5分,共25分)
13. 分解因式: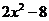
15. 解方程: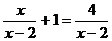
16.已知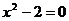 ,求代数式
,求代数式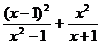 的值.
的值.
17.如图,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG.
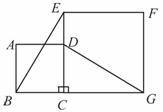
(1)求证:BE=DG;
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说出旋转过程;若不存在,请说明理由.
四、解答题(共2个小题,共10分)
18.(本小题满分5分)
19.(本小题满分5分)
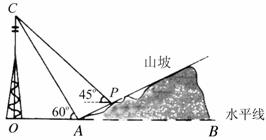
如图,某人在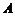 处测得电视塔尖点
处测得电视塔尖点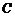 的仰角为
的仰角为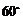 ,沿山坡向上走到
,沿山坡向上走到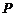 处,测得点
处,测得点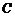 的仰角为
的仰角为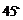 ,已知
,已知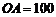 米,山坡坡度为
米,山坡坡度为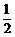 (即
(即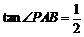 )且点O、A、B在同一条直线上.求电视塔
)且点O、A、B在同一条直线上.求电视塔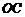 的高度以及此人所在位置点
的高度以及此人所在位置点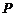 到OB的距离.(测倾器的高度忽略不计,结果保留根号形式).
到OB的距离.(测倾器的高度忽略不计,结果保留根号形式).
五、解答题(本题满分6分)
20.已知菱形ABCD中,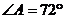 ,请设计三种不同的分法,将菱形ABCD分割成四个三角形,使得分割成的每个三角形都是等腰三角形(画图工具不限,要求画出分割线段;标出能够说明不同分法所得三角形的内角度数,例如图,不要求写出画法,不要求证明.)注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.
,请设计三种不同的分法,将菱形ABCD分割成四个三角形,使得分割成的每个三角形都是等腰三角形(画图工具不限,要求画出分割线段;标出能够说明不同分法所得三角形的内角度数,例如图,不要求写出画法,不要求证明.)注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.
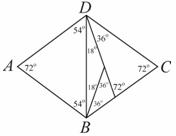
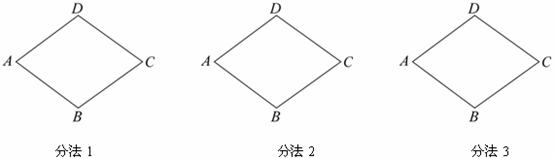
六、解答题(共2个小题,共9分)
21.(本题满分4分)
为了进一步了解学生的身体素质情况体育老师对初三年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
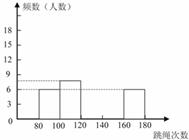
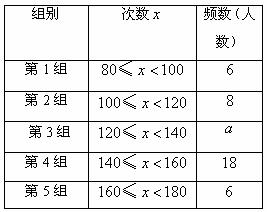
请结合图表完成下列问题:
(1)表中的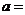 ;
;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)若初三年级学生一分钟跳绳次数(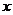 )达标要求是:
)达标要求是: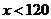 为不合格;
为不合格;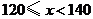 为合格;
为合格;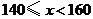 为良;
为良;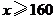 为优。根据以上信息,请你给学校或初三年级同学提一条合理化建议:
为优。根据以上信息,请你给学校或初三年级同学提一条合理化建议:
.
22.(本题满分5分)
某肉食加工厂在烤制风味肠时主要依据的是下面表格中的数据:
风味肠的质量/千克
0.5
1
1.5
2
2.5
3
3.5
4
烤制时间/分
8
12
16
20
24
28
32
36
根据以上表格所提供的信息回答:
(1)当烤制的风味肠的质量为
(2)当烤制的风味肠的质量为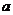 千克时,需要烤制时间是多少分钟?
千克时,需要烤制时间是多少分钟?
七、解答题((本题满分7分)
23.已知二次函数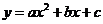 的图象和x轴有且只有一个交点A,与y轴的交点为
的图象和x轴有且只有一个交点A,与y轴的交点为
B(0,4),且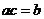 .
.
(1)求该二次函数的解析表达式;
(2)将一次函数y=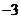 x的图象作适当平移,使它经过点A,记所得的图象为L,图象L与抛物线的另一个交点为C,求△ABC的面积.
x的图象作适当平移,使它经过点A,记所得的图象为L,图象L与抛物线的另一个交点为C,求△ABC的面积.
八、解答题(本题满分7分)
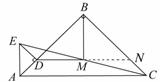
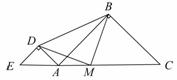
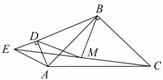
24.如图,已知点D在AC上,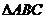 和
和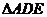 都是等腰直角三角形,点M为EC的中点.
都是等腰直角三角形,点M为EC的中点.
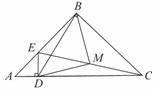
(1)求证: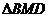 为等腰直角三角形.
为等腰直角三角形.
(2)将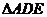 绕点A逆时针旋转
绕点A逆时针旋转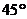 ,如图,(1)中的“
,如图,(1)中的“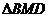 为等腰直角三角形”是否仍然成立?请说明理由.
为等腰直角三角形”是否仍然成立?请说明理由.
(3)将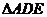 绕点A逆时针旋转
绕点A逆时针旋转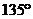 ,如图,(1)中的“
,如图,(1)中的“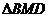 为等腰直角三角形”成立吗?(不用说明理由)
为等腰直角三角形”成立吗?(不用说明理由)
(4)我们是否可以猜想,将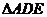 绕点A任意旋转一定的角度,如图24-4,(1)中的“
绕点A任意旋转一定的角度,如图24-4,(1)中的“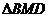 为等腰直角三角形”均成立?(不用说明理由).
为等腰直角三角形”均成立?(不用说明理由).
九、解答题(本题满分8分)
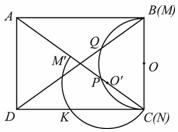
25.矩形ABCD中,AD=2,2 < AB < 4 ,现将一个直径MN为2的量角器如图摆放,使其 线的端点N与C重合,M与B重合,O为MN的中点,量角器的半圆弧与矩形ABCD的对角线AC、BD分别交于P、Q,设P、Q在量角器上的读数分别是
线的端点N与C重合,M与B重合,O为MN的中点,量角器的半圆弧与矩形ABCD的对角线AC、BD分别交于P、Q,设P、Q在量角器上的读数分别是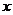 、
、 .
.
(1)求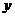 与
与 之间的函数关系式.(不必写出自变量的取值范围).
之间的函数关系式.(不必写出自变量的取值范围).
(2)将量角器绕C点逆时针旋转,使它的直径落在AC上,如下图所示,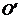 为
为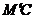 的中点,此时量角器的半圆弧交DC于K,若K点的读数为
的中点,此时量角器的半圆弧交DC于K,若K点的读数为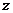 ,那么
,那么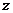 与
与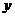 的数量关系是什么,请说明理由.
的数量关系是什么,请说明理由.
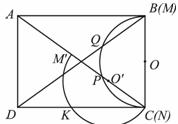
(3)如下图所示,若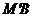 ‖
‖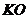 ,求出此时AB的长.
,求出此时AB的长.
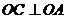
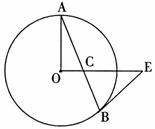
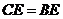 时,直线BE与⊙O有怎样的位置关系?请说明理由.
时,直线BE与⊙O有怎样的位置关系?请说明理由.