2008-2009学年度菏泽郓城县第一学期初二教学质量检测
数学试卷
一、选择题(每小题给出的四个选项中,只有一个是正确的。每小题2分,共20分)
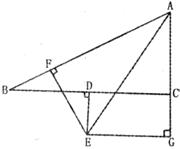
1.如下图,AB=CD,AE⊥BD于E,CF⊥BD于F,AE=CF,则图中全等的三角形有
A.1对 B.2对 C.3对 D.4对
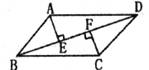
2.如下图,BA=BC,DA=DC,则判定△ABD和△CBD的依据是
A.SSS B.ASA C.HL D.SAS
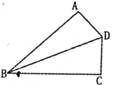
3.如下图,△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,则下列结论错误的是
A.BD+DE=BC B.DE平分∠ADB C.AD平分∠EDC D.DE+A>AD
4.下列轴对称图形中,对称轴条数最多的是
A.长方形 B.正方形 C.正五边形 D.圆
5.一个等腰三角形的一边长
A.
6.下列各式无意义的是
A.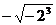 B.
B.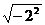 C.
C.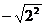 D.
D.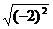
7.0.16的平方根是
A.0.4 B.±
8.在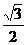 ,
,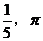 ,
,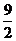 ,0.505005000,无理数的个数为
,0.505005000,无理数的个数为
A.2个 B.3个 C.4个 D.5个
9.下列计算正确的是
A.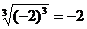 B.
B.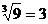 C.
C. 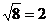 D.
D.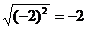
10.如果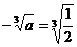 ,则
,则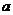 的值是
的值是
A.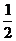 B.
B.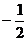 C.
C.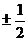 D.
D.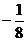
二、填空题(每空3分,共30分)
1.如果9的平方根是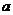 ,
, ,则
,则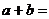 __________。
__________。
2.已知点A(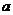 ,-2)与点B(
,-2)与点B(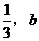 )关于
)关于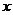 轴对称,则
轴对称,则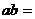 __________。
__________。
3.一个数的平方根是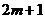 和
和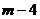 ,则这个数是__________。
,则这个数是__________。
4.如下图,△ABC中,已知AB=AC,要使AD=AE,需要添加的一个条件是(只需添加一个即可)__________。
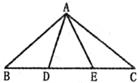
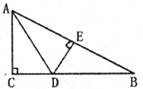
5.如下图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=
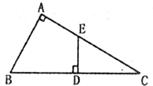
6.如下图,△ABC中,∠B、∠C的平分线交于P,PD∥AB,PE∥AC,如果BC=
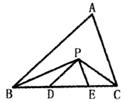
7.如下图,已知BE⊥AD,CF⊥AD,且BE=CF,那么AD是△ABC的中线还是角平分线?__________。
8.如下图,笔直的公路旁有A、B两车站,相距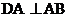 于A,CB⊥AB于B,DA=
于A,CB⊥AB于B,DA=
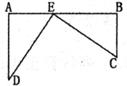
9.若点P关于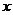 轴的对称点的坐标为(
轴的对称点的坐标为(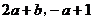 ),关于
),关于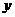 轴对称点的坐标为(
轴对称点的坐标为(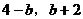 ),则
),则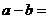 __________。
__________。
10.如下图所示是一块三角形田地,AB=AC=

三、计算(每小题4分,共12分)
1. 2.
2.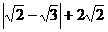 3.
3.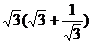
小丽想用一块面积为
五、(本题8分)
证明:如果两个三角形有两条边和其中一边上的中线对应相等,那么这两个三角形全等。(提示:先写出已知和求证,然后根据题意画出图形后再证明)
六、(本题8分)
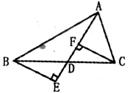
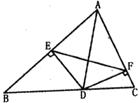
如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,求证:AD垂直平分EF。
四、(本题8分)
七、(本题8分)
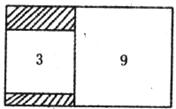
如下图所示,长方形内有两个相邻的正方形,面积分别为
八、(本题10分)
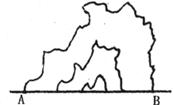
某铁路施工队在建设铁路的过程中要打通一座小山,需要测量隧道AB的长,恰好山的周围是宽阔的平地。请你利用三角形全等的知识帮助测量人员测量出AB的长,简要说明测量的方法,画出测量方案,说明方案合理的理由。
九、(本题10分)
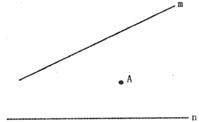
某公路管理员的居住点A位于两条公路m、n之间,他要在公路m、n的旁边分别建一个公路管理房,使他从居住点A出发,先到公路m的公路管理房再到公路n的公路管理房,然后回到居住点的距离总和最短,请你帮他画出在公路m和公路n的公路管理房的建筑位置(如下图,要求:画出图形,保留作图痕迹,不要求写出作法和证明)
十、(本题10分)
如图,△ABC中,D为BC的中点,DE⊥BC交∠ BAC的平分线于E,EF⊥AB,交AB于F,EG⊥AC,交AC的延长线于G,试问:BF与CG的大小如何?证明你的结论。