2008-2009学年度淄博市淄川区第一学期初四期中教学评价
数学试卷
本试题分第Ⅰ卷和第Ⅱ卷两部分。第Ⅰ卷为选择题,36分;第Ⅱ卷为非选择题,84分;共120分,考试时间为120分钟。
第Ⅰ卷(选择题 共36分)
一、选择题:本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,每题3分,错选、不选或选出的答案超过一个,均记0分。
1.如下图所示,梯子与地面的夹角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是
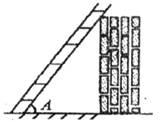
A.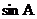 的值越小,梯子越陡
的值越小,梯子越陡
B.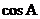 的值越小,梯子越陡
的值越小,梯子越陡
C.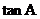 的值越小,梯子越陡
的值越小,梯子越陡
D.梯子的陡缓程度与∠A的三角函数值无关
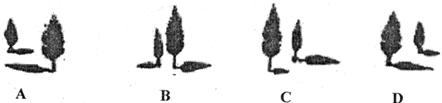
2.下列四幅图形中,表示两颗小树在同一时刻阳光下的影子的图形可能是
3.在△ABC中,∠C=90°,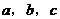 分别表示∠A,∠B,∠C的对边,给出以下结论:
分别表示∠A,∠B,∠C的对边,给出以下结论:
①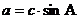 ; ②
; ②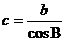 ;
;
③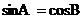 ; ④如果
; ④如果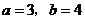 ,那么
,那么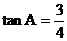 。
。
其中正确的个数是
A.1 B.
4.函数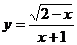 的自变量
的自变量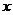 的取值范围是
的取值范围是
A.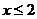 B.
B.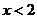
C.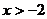 且
且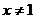 D.
D.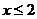 且
且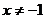
5.下列函数关系中,可以看作二次函数 模型的是
模型的是
A.在一定距离内,汽车行驶的速度与行驶的时间的关系
B.我国人口自然增长率为1%,这样我国总人口数随年份变化的关系
C.矩形周长一定时,矩形面积和矩形边长之间的关系
D.圆的周长与半径之间的关系
6.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是斜边AB上的一点,且AD=5,则∠BCD的正切值是
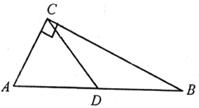
A.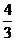 B.
B.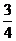 C.
C.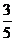 D.
D.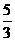
7.已知二次函数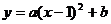 有最小值是-1,则
有最小值是-1,则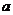 与
与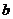 之间的大小关系是
之间的大小关系是
A.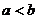 B.
B.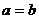 C.
C.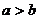 D.不能确定
D.不能确定
8.一张桌子上重叠摆放了若干枚面值为1元的硬币,它的三视图如图所示,则桌子上共有1元硬币
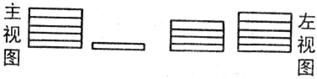
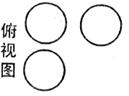
A.11枚 B.10枚 C.9枚 D.8枚
9.在同一坐标平面内,图像不可能由函数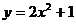 的图像通过平移变换、轴对称变换得到的函数是
的图像通过平移变换、轴对称变换得到的函数是
A.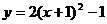 B.
B.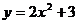
C. D.
D.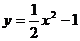
10.根据下表可知,二次函数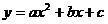 的表达式是
的表达式是
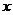
-1
0
1
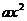
1
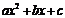
8
3
A.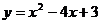 B.
B.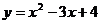
C.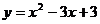 D.
D.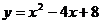
11.如果用□表示1个立方体,用 表示两个立方体叠加,用■表示三个立方体叠加,那么下面左图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是
表示两个立方体叠加,用■表示三个立方体叠加,那么下面左图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是
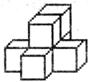
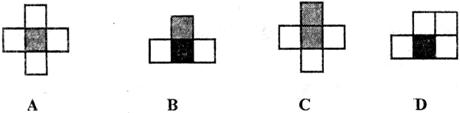
12.某学校的围墙上端由一段段相同的拱形栅栏组成,如下图所示,其拱形图为抛物线的一部分,在栅栏的最大跨度AB间,按相同的间距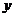 轴建立平面直角坐标系,根据以上的数据,则每段栅栏所需立柱的总长度约为( )米(精确到
轴建立平面直角坐标系,根据以上的数据,则每段栅栏所需立柱的总长度约为( )米(精确到
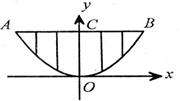
A.1.5 B.
第Ⅱ卷(非选择题 共84分)
二、填空题:本题共5小题,满分20分,只要求填写最后结果,每小题填对,得4分。
13.已知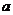 为等边三角形的一个内角,则
为等边三角形的一个内角,则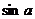 的值为___________。
的值为___________。
14.如下图,钓鱼竿AC长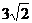 米,钓鱼者想看看鱼上钩的情况,把钓鱼杆AC转动到
米,钓鱼者想看看鱼上钩的情况,把钓鱼杆AC转动到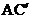 的位置,此时露在水面上的鱼线
的位置,此时露在水面上的鱼线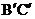 长为
长为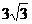 米,则鱼杆转过的角是___________度。
米,则鱼杆转过的角是___________度。
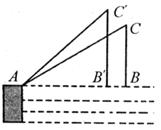
15.如下图是由四个相同的小立方体组成的立体图形的主视图和左视图,那么原立体图形可能是___________(把下图中正确的立体图形的序号都填在横线上)。
16.若抛物线 的对称轴为直线
的对称轴为直线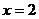 ,最小值为-2,则关于
,最小值为-2,则关于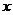 的方程
的方程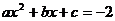 的根为___________。
的根为___________。
17.已知二次函数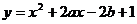 和
和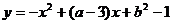 的图像都经过
的图像都经过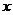 轴上两个不同的点M,N,则
轴上两个不同的点M,N,则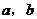 的值依次为___________。
的值依次为___________。
三、解答题:本大题共8小题,共64分。解答要写出必要的文字说明、证明过程或演算步骤。
18.(本题满分6分)确定图中路灯灯泡的位置,并画出小赵在灯光下的影子。
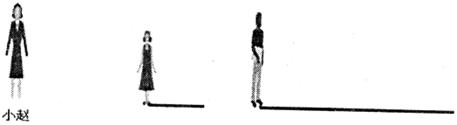
19.(本题满分7分)补全下列物体的三视图。
(1)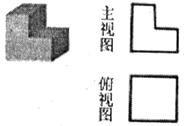 (2)
(2)
20.(本题满分8分)已知抛物线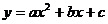 经过点(-1,-1),(0,-2),(1,1)。
经过点(-1,-1),(0,-2),(1,1)。
(1)求这条抛物线的解析式;
(2)用配方法确定抛物线的对称轴和顶点坐标;
(3)这个函数有最大值还是最小值?这个值是多少?
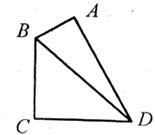
21.(本题满分8分)在四边形ABCD中,∠DAB=∠BCD=90°,∠ADC=60°,AB=2,BC=11,求BA的长。
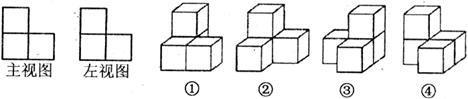
22.(本题满分8分)如下图所示,某学校拟建两幢平行的教学楼,现设计两楼相距
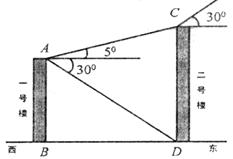
(1)求两幢楼分别高多少米?(结果精确到
(2)若冬日上午9:00太阳光的入射角最低为30°(光线与水平线的夹角),问一号楼的光照是否会有影响?请说明理由,若有,则两楼间距离应至少相距多少米时才会消除这种影响?(结果精确到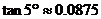 ,
,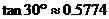 )
)
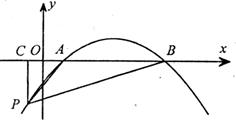
23.(本题满分9分)如下图,抛物线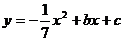 和
和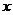 轴相交于A,B两点,AB=4,P为抛物线上的一点,
轴相交于A,B两点,AB=4,P为抛物线上的一点,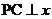 轴于点C,C点的横坐标为-1,∠PAC=45°,
轴于点C,C点的横坐标为-1,∠PAC=45°,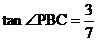 。试求抛物线的解析式。
。试求抛物线的解析式。
24.(本题满分9分)某海滨浴场的海岸可以看作是直线,如下图所示(MN表示海岸线),三位救生员在岸边的点A看到大海中的点B有人求救,便同时展开救助。一号救生员直接从点A游到点B救人;二号救生员从点A沿海岸跑到点C,然后从点C游到点B救人;三号救生员沿海岸向前跑 ,
,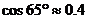 ,
,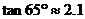 ,
,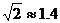 )
)

25.(本题满分9分)在某次数字变换游戏中,我们把0,1,2,3,4,5,6,7,...100称为“旧数”,游戏的变换规则是:将旧数先平方,再除以100,所得的数称为“新数”。
(1)请把旧数80和26按照上述规则变换为新数;
(2)经过上述规则变换后,我们发现许多“旧数”变小了。有人断言:“按照上述变换规则,所有的‘新数’都不等于它的‘旧数’”,你认为这种说法对吗?若不对,请求出所有不符合这一说法的旧数;
(3)请求出按照上述规则变换后减小得最多的旧数(要写如解答过程)。