2008-2009学年度滨州市滨城区第一学期九年级期中学业水平测试
数学试卷
一、选择题(每小题4分,共40分)将正确答案的代号填入答题卡栏
1.下列关于x的方程中,是一元二次方程的有( )
A.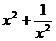 B.
B.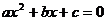
C.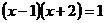 D.
D.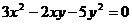
2.化简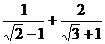 的结果为( )
的结果为( )
A. B.
B. C.
C.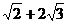 D.
D.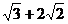
3.在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转.下列图案中,不能由一个图形通过旋转而构成的是( )

4.要使二次根式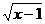 有意义,那么x的取值范围是( )
有意义,那么x的取值范围是( )
A. x>-1 B.x<
5.已知圆锥的底面半径为3,高为4,则圆锥的侧面积为( )
A. 10π B. 12π C.15π D.20π
6.已知x、y是实数,+y2-6y+9=0,则xy的值是( )
A.4 B.-
7.如下图,在一幅长
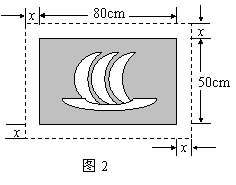
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
8.如下图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为( )
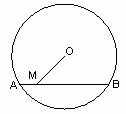
A.2 B.
9.已知:如下图, ⊙O的两条弦AE、BC相交于点D,连接AC、BE. 若∠ACB=60°,则下列结论中正确的是( )
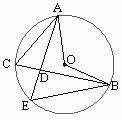
A.∠AOB=60° B. ∠ADB=60°
C.∠AEB=60° D.∠AEB=30°
10正六边形的外接圆的半径与内切圆的半径之比为( )
A.1: B.
B. :
: D.
D. :1
:1
二、填空题(每小题4分,共40分)
11.方程(2x-1)(3x+1)=x2+2化为一般形式为____________,其中a=__ _,b=__ __,c=____.
12.方程 x 2 = x 的解是______________________
13.实数a在数轴上的位置如下图所示,化简: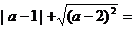 。
。
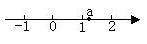
14.若实数a、b满足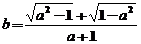 则a+b的值为________.
则a+b的值为________.
15.圆和圆有不同的位置关系.与下图不同的圆和圆的位置关系有_____.(只填一种)
16.若方程kx2?6x+1=0有两个实数根,则k的取值范围是 .
17.已知一条弧的长是 厘米
厘米
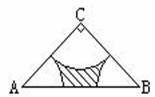
18.如图,在Rt△ABC中,∠C=90°,CA=CB=2。分别以A、B、C为圆心,以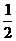 AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是______.
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是______.
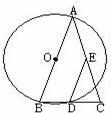
19.已知:如下图,等腰三角形ABC中,AB=AC=4,若以AB为直径的⊙O与BC相交于点D,DE∥AB,DE与AC相交于点E,则DE=____________。
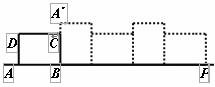
20.已知矩形ABCD的长AB=4,宽AD=3,按如下图放置在直线AP上,然后不滑动地转动,当它转动一周时( A →A′),顶点A所经过的路线长等于 。
三.解答题(共18分)
21.(4分)计算: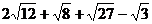
22.(6分)某次商品交易会上,所有参加会议的商家之间都签订了一份合同,共签订合同36份,求共有多少商家参加了交易会?
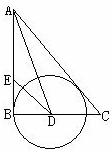
23.(8分)如下图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆。
求证:(1)AC是⊙D的切线;(2)AB+EB=AC。
四、应用题(10分)
24.某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.
五、综合题(12分)
25.高致病性禽流感是比SARS病毒传染速度更快的传染病。
(1)某养殖场有8万只鸡,假设有1只鸡得了禽流感,如果不采取任何防治措施,那么,到第二天将新增病鸡10只,到第三天又将新增病鸡100只,以后每天新增病鸡数依次类推,请问:到第四天,共有多少只鸡得了禽流感病?到第几天,该养殖场所有鸡都会被感染?
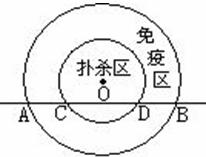
(2)为防止禽流感蔓延,政府规定:离疫点