2008年苏州市初中毕业暨升学考试
数学试卷
一、填空题:本大题共12小题,每小题3分,共36分。把答案直接填在题目相对应的位置上。
1.-5的相反数是 。
2.计算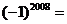 。
。
3.某校初一年级在下午3:00开展“阳光体育”活动。下午3:00这一时刻,时钟上分针与时针所夹的角等于 度。
4.函数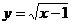 中,自变量
中,自变量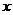 的取值范围是 。
的取值范围是 。
5.分解因式: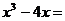 。
。
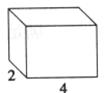
6.如下图,水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于 。
7.小明在7次百米跑练习中成绩如下:
次数
第一次
第二次
第三次
第四次
第五次
第六次
第七次
成绩(秒)
12.8
12.9
13.0
12.7
13.2
13.1
12.8
这7次成绩的中位数是 秒。
8.为迎接2008年北京奥运会,小甜同学设计了两种乒乓球,一种印有奥运五环图案,另一种印有奥运福娃图案。若将8个印有奥运五环图案和12个印有奥运福娃图案的乒乓球放入一个空袋中,且每个球的大小相同,搅匀后在口袋中随机摸出一个球,则摸到印有奥运五环图案的球的概率是 。
9.关于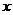 的一元二次方程
的一元二次方程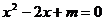 有两个实数根,则
有两个实数根,则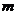 的取值范围是
。
的取值范围是
。
10.将一个边长为1的正八边形补成如下图所示的正方形,这个正方形的边长等于 _______(结果保留根号)。
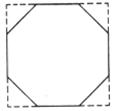
11.
12.初三数学课本上,用“描点法”画二次函数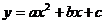 的图像时,列了如下表格:
的图像时,列了如下表格:
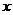
…
-2
-1
0
1
2
…
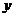
…
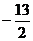
-4

-2

…
根据表格上的信息回答问题:该二次函数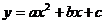 在
在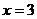 时,
时,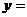 。
。
二、选择题:本大题共6小题,每小题3分,共18分。在每小题给出的四个选项中,只有一项是符合题目要求的。
13.下列运算正确的是
A.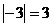 B.
B.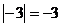 C.
C.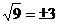 D.
D.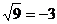
14.函数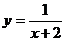 中,自变量
中,自变量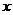 的取值范围是
的取值范围是
A.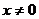 B.
B.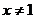 C.
C.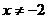 D.
D.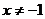
15.据苏州市《城市商报》
A.1.5×106 B.1.5×
16.下列图形中,为轴对称图形的是

17.若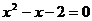 ,则
,则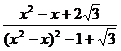 的值等于
的值等于
A.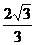 B.
B.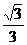 C.
C.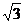 D.
D.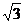 或
或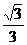
18.如下图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°。现给出以下四个结论:

①∠A=45° ②AC=AB ③弧AE=弧BE ④CE?AB=2BD2
其中正确结论的序号是
A.①② B.②③ C.②④ D.③④
三、解答题:本大题共11小题,共76分。把解答过程写在相对应的位置上,解答时应写出必要的计算过程、推演步骤或文字说明。
19.(本题5分)
计算: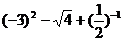
20.(本题5分)
先化简,再求值: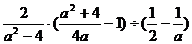 ,其中
,其中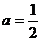
21.(本题5分)
解方程: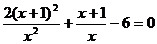
22.(本题6分)
解不等式组: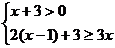 ,并判断
,并判断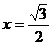 是否满足该不等式组。
是否满足该不等式组。
23.(本题6分)
如下图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4。
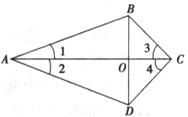
求证:(1)△ABC≌△ADC;
(2)BO=DO。
24.(本题6分)
某厂生产一种产品,图甲是该厂第一季度三个月产量的统计图,图乙是这三个月的产量与第一季度总产量的比例分布统计图,统计员在制作图甲、图乙时漏填了部分数据。
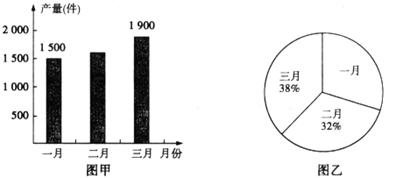
根据上述信息,回答下列问题:
(1)该厂第一季度哪一个月的产量最高? 月。
(2)该厂一月份产量占第一季度总产量的 %。
(3)该厂质检科从第一季度的产品中随机抽样,抽检结果发现样品的合格率为98%。请你估计:该厂第一季度大约生产了多少件合格的产品?(写出解答过程)
25.(本题8分)
如下图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于O点。训练时要求A、B两船始终关于O点对称。以O为原点,建立如图所示的坐标系,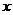 轴、
轴、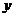 轴的正方向分别表示正东、正北方向。设A、B两船可近似看成在双曲线
轴的正方向分别表示正东、正北方向。设A、B两船可近似看成在双曲线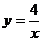 上运动,湖面风平浪静,双帆远影优美.训练中当教练船与A、B两船恰好在直线
上运动,湖面风平浪静,双帆远影优美.训练中当教练船与A、B两船恰好在直线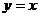 上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示)。
上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示)。
(1)发现C船时,A、B、C三船所在位置的坐标分别为A( , )、B( , )和C( , );
(2)发现C船,三船立即停止训练,并分别从A、O、B三点出发沿最短路线同时前往救援,设A、B两船的速度相等,教练船与A船的速度之比为3┱4,问教练船是否最先赶到?请说明理由。
26.(本题8分)
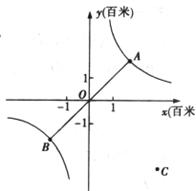
如下图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12。动点P从D点出发沿DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动。两点同时出发,当P点到达C点时,Q点随之停止运动。
(1)梯形ABCD的面积等于 ;
(2)当PQ∥AB时,P点离开D点的时间等于 秒:
(3)当P、Q、C三点构成直角三角形时,P点离开D点多少时间?
27.(本题9分)
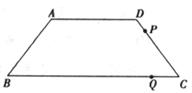
如图,在△ABC中,∠BAC=90°,BM平分∠ABC交AC于M,以A为圆心,AM为半径作⊙A交BM于N,AN的延长线交BC于D,直线AB交⊙A于P、K两点,作MT⊥BC于T。
(1)求证AK=MT;
(2)求证:AD⊥BC;
(3)当AK=BD时.求证: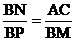
28.(本题9分)
课堂上,老师将图甲中△AOB绕O点逆时针旋转,在旋转中发现图形的形状和大小不变,但位置发生了变化,当△AOB绕点O逆时针旋转90°时,得到△A1OB1。已知A(4,2)、B(3,0)。
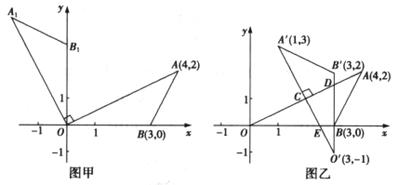
(1)△A1OB1的面积是 ;A1点的坐标为( , );B1点的坐标为( , );
(2)课后,小玲和小惠对该问题继续进行探究,将图乙中△AOB绕AO的中点C(2,1)逆时针旋转90°得到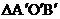 ,设
,设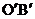 交OA于D,
交OA于D,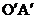 交
交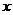 轴于E,此时
轴于E,此时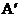 、
、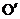 和
和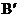 的坐标分别为(1,3)、(3,-1)和(3,2),且
的坐标分别为(1,3)、(3,-1)和(3,2),且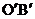 经过B点。在刚才的旋转过程中,小玲和小惠发现旋转中的三角形与△AOB重叠部分的面积不断变小,旋转到90°时重叠部分的面积(即四边形CEBD的面积)最小,求四边形CEBD的面积;
经过B点。在刚才的旋转过程中,小玲和小惠发现旋转中的三角形与△AOB重叠部分的面积不断变小,旋转到90°时重叠部分的面积(即四边形CEBD的面积)最小,求四边形CEBD的面积;
(3)在(2)的条件下,△AOB外接圆的半径等于 。
29.(本题9分)
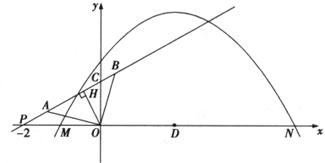
如下图,抛物线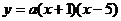 与
与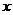 轴的交点为M、N,直线
轴的交点为M、N,直线 与
与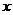 轴交于P(-2,0),与
轴交于P(-2,0),与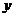 轴交于C,若A、B两点在直线
轴交于C,若A、B两点在直线 上,且AO=BO=
上,且AO=BO=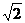 ,AO⊥BO,D为线段MN的中点,OH为Rt△OPC斜边上的高。
,AO⊥BO,D为线段MN的中点,OH为Rt△OPC斜边上的高。
(1)OH的长度等于 ;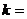 ,
,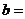 。
。
(2)是否存在实数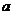 ,使得抛物线
,使得抛物线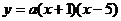 上有一点E,满足以D、N、E为顶点的三角形与△AOB相似?若不存在,说明理由;若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由)。并进一步探索对符合条件的每一个E点,直线NE与直线AB的交点G是否总满足
上有一点E,满足以D、N、E为顶点的三角形与△AOB相似?若不存在,说明理由;若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由)。并进一步探索对符合条件的每一个E点,直线NE与直线AB的交点G是否总满足 ,写出探索过程。
,写出探索过程。