2007-2008学年度烟台市招远第二学期初二期末考试
数学试卷
说明:
1.本试卷试题共115分;
2.书写质量3分;
3.卷面安排2分;
整个试卷满分为120分。
一、选择题:(每小题2分,满分30分)
1.数据5,3,2,1,4的平均数是
A.2 B.3 C.4 D.5
2.已知 ,则下列不等式成立的是
,则下列不等式成立的是
A. B.
B.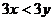
C.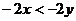 D.
D.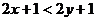
3.下列各式由左边到右边的变形,是分解因式的为
A.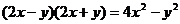 B.
B.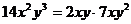
C.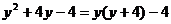 D.
D.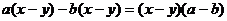
4.菱形的边长为5,一条对角线的长为8,则另一条对角线长为
A.3 B.4 C.6 D.8
5.已知一组数据 ,5,0,3,1,-1的平均数
,5,0,3,1,-1的平均数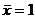 ,那么它的中位数是
,那么它的中位数是
A.0 B.2.5 C.1 D.0.5
6.若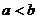 ,且
,且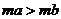 ,则
,则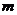 应满足的条件是
应满足的条件是
A.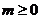 B.
B.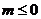 C.
C.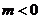 D.
D.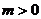
7.分解因式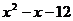 的结果是
的结果是
A.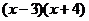 B.
B.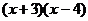
C.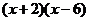 D.
D.
8.如下图,面积为
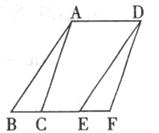
A.
9.国家实行一系列“三农”优惠政策后,农民收入大幅度增加,某镇所辖村庄去年年人均收入情况如下表所示:
年人均收入(元)
3500
3700
3800
3900
4500
村庄个数(个)
1
1
3
3
1
则该镇所辖村庄去年年人均收入的中位数是
A.3700元 B.3800元 C.3850元 D.3900元
10.解集在数轴上表示为如下图所示的不等式组是

A.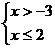 B.
B.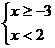 C.
C.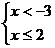 D.
D.
11.计算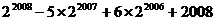 的值为
的值为
A.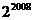 B.2008 C.0 D.
B.2008 C.0 D.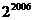
12.如下图,在△MBN中,BM=
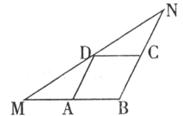
A.
13.不等式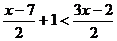 的负整数解有
的负整数解有
A.1个 B.2个 C.3个 D.无数个
14.如下图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为
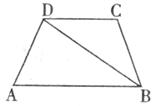
A.
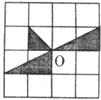
15.如下图,将方格纸中的图形绕点O顺时针旋转90°后得到的图形是

二、填空题:(将正确答案填在横线上。每小题3分,满分30分)
16.若数据3,4,5,6, 的众数为3,则这组数据的中位数是
的众数为3,则这组数据的中位数是
17.写出一个能运用公式法进行分解因式的三项式
18.不等式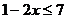 的解集为
的解集为
19.分解因式
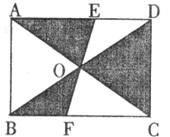
20.如下图,矩形ABCD的对角线相交于点O,过点O的直线分别交AD、BC于点E、F,若AB=
21.当 时,代数式
时,代数式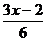 的值为非负数。
的值为非负数。
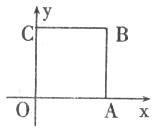
22.如下图,边长为1的正方形OABC的顶点A、C在坐标轴上,顶点O与原点重合,顶点B在第一象限,则该正方形绕点O逆时针旋转45°后,B点的坐标为
23.如图,当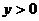 时,自变量
时,自变量 的取值范围是
的取值范围是

24.为了解学校用水情况,小新同学在4月份连续观察了5天学校的:水表(每天都是上午8点钟观察),并进行记录如下:
日期
1日
2日
3日
4日
5日
水表示数(m3)
121
123
126
128
131
请运用学过的知识,估计小新学校4月份(30天)用水量是 m3。
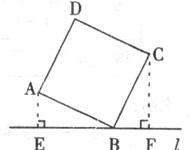
25.如下图,直线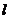 过正方形ABCD的顶点B,点A、C到直线
过正方形ABCD的顶点B,点A、C到直线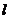 的距离分别是1和2,则正方形的边长是 。
的距离分别是1和2,则正方形的边长是 。
三、解答题:(每题10分,满分20分)
26.(1)解不等式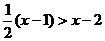 ,并把它的解集表示在数轴上。
,并把它的解集表示在数轴上。
(2)解不等式组:
27.把下列各式分解因式:
(1)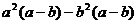
(2)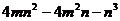
四、解释与说明题:(每题8分,满分16分)
28.爱华公司有10名销售员,去年完成销售额情况如下表:
销售额(万元)
3
4
5
6
7
8
10
销售员人数(人)
1
3
2
1
1
1
1
(1)求销售额的平均数、众数、中位数。
(2)今年公司为了调动员工的积极性,提高年销售额,准备采取超额有奖的措施。请根据(1)的结果,通过比较,合理确定今年每个销售员统一的销售额标准。
29.如下图,在梯形ABCD中,AB∥DC,DA⊥DC,∠B=45°,延长CD到点E,使DE=DA,连接AE。
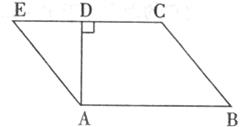
(1)说明AE∥BC;
(2)若AB=
五、探索题:(满分9分)
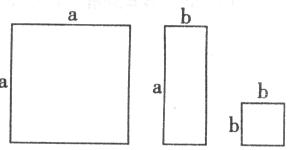
30.给你若干个矩形和正方形卡片,如下图所示,请你用拼图的方法,拼成一个大矩形,使它的面积等于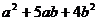 ,并根据你拼成的图形分解因式
,并根据你拼成的图形分解因式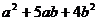 。
。
六、实际应用题:(满分10分)
31.某校准备组织290名学生进行野外考察活动,行李共有100件。学校计划租用甲、乙两种型号的汽车共8辆,经了解,甲种汽车每辆最多能载40人和l0件行李,乙种汽车每辆最多能载30人和20件行李.请你帮助学校设计所有可能的租车方案。