2008年临沂市费县九年级学业水平测试模拟训练
数学试卷
一.选择题(本大题共14小题,每小题3分,共42分)在每小题给出的四个选项中,只有一项是符合题目要求的.
1.-2的相反效是( ).
A.-2 B.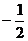 D.
D.
2.下列运算正确的是( ).
A.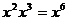 B.
B.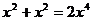 C.
C.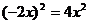 D.
D.
3.如图,已知AB//CD.则( ).
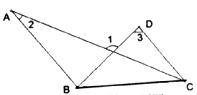
A.∠1=∠2+∠3 B.∠1=2∠2+∠3
C.∠1=2∠2-∠3 D.∠1=180°-∠2-∠3
4.若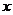 =3,
=3,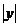 =5,则
=5,则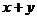 的值( ).
的值( ).
A.-8 B.-
5.如果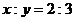 ,则下列各式不成立的是( ).
,则下列各式不成立的是( ).
A.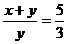 B.
B.
C.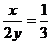 D.
D.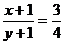
6.如图,梯形ABCD中,AD//BC,AC为对角线,E为DC中点,AE、BC的延长线交于G点,则图中相等的线段共有( ).
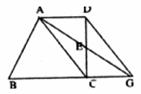
A.2对 B.3对 C.4对 D.5对
7.如果经过圆锥的轴的剖面是一个边长为
A.8 B.
B.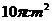 C.
C.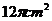 D.
D.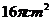
8.下列可能是正方体展开图的是( )


9.如图,D为AABC的AB边上的一点,∠DCA=∠B,若AC=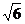 cm,AB=
cm,AB=
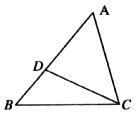
A.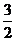 cm B.
cm B. cm C.
cm C.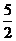 cm
cm
10.若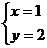 是方程
是方程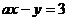 的解,则
的解,则 的取值是( )
的取值是( )
A.5 B.-
11.如图,在平面直角坐标系中,A点坐标为(3,4),将OA绕原点O逆时针旋转90°得到OA’,则点A’的坐标是( )
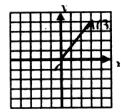
A.(-4,3) B.(-3,4) C.(3,-4) D.(4,-3)
12.若A(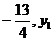 ),B(
),B(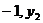 ),C(
),C( )为二次函数
)为二次函数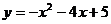 的图象上的三点,则y1、y2、y3的大小关系是( )
的图象上的三点,则y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y
13.如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=3,OA=4,则cos∠APO的值为( )
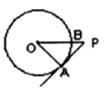
A.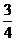 B.
B.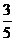 C.
C.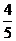 D.
D.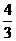
14.如图,这是一个跳棋盘,其中格点上的黑色点为棋子,剩余的格点上没有棋子.我们约定跳棋游戏的规则是:把跳棋棋子在棋盘内沿直线隔着棋子对称跳行,跳行一次称为一步.已知点A为已方一枚棋子,欲将棋子A跳进对方区域(阴影部分的格点),则跳行的最少步数为( )
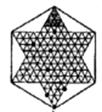
A.2步 B.3步 C.4步 D.5步
二.填空题(本大题共5个小题;每小题3分,共15分)把答案写在题中横线上.
15.分解因式: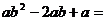 .
.
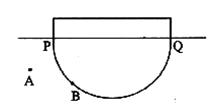
16.如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻.当他带球冲到A点时,同伴乙已经助攻冲到B点.有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.仅从射门角度考虑,应选择 种射门方式.
17.某品牌电饭锅成本价为70元,销售商对其销量与定价的关系进行了调查,结果如下:
定价(元)
100
110
120
130
140
150
销量(个)
80
100
110
100
80
60
为获得最大利润,销售商应将该品牌电饭锅定价为 元.
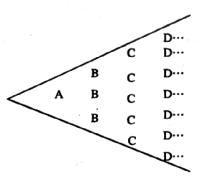
18.如下图,按英文字母表A、B、C、D、E、F、G、…顺序有规律排列而成鱼状图案中,字母“G'’出现次数为 .
19.一个“QQ”群里共有若干个好友,每个好友都分别给群里其他好友发送一条信息,这样共有870条信息,在这个“QQ”群里有 个好友.
三.解答题(本大题共7个小题;共63分)
20.(本题满分7分)小颖为九年级l班毕业联欢会设计了一个“配紫色”的游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,两个转盘停止转动时,若有一个转盘的指针指向蓝色,另一个转盘的指针指向红色,则“配紫色”成功,游戏者获胜.求游戏者获胜的概率.

21.(本题满分8分)如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交⊙O于D.
(1)请写出四个不同类型的正确结论;
(2)若BC=8,ED=2,求⊙O的半径.
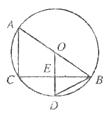
22.(本题满分8分)如图,已知反比例函数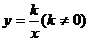 图象经过点A(
图象经过点A(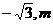 ),过点A作AB
),过点A作AB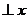 轴于点B,且△AOB的面积为
轴于点B,且△AOB的面积为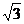 .(1)求
.(1)求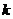 和
和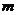 的值;(2)若一次函数
的值;(2)若一次函数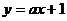 的图象经过点A,且与
的图象经过点A,且与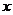 轴相交于点C,,求|AO|:|AC|的值。
轴相交于点C,,求|AO|:|AC|的值。
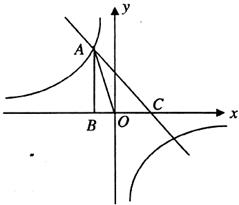
23.(本小题满分8分)如图,在正六边形ABC,BF相交于点M,BD与CE相交于点N.
(1)观察图形,写出图中两个不同形状的特殊四边形;
(2)选择(1)中的一个结论加以证明.
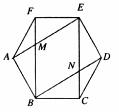
24、(本题满分10分)如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4。
(1)求证:△ABE∽△ADB,并求AB的长;
(2)延长DB到F,使BF=BO,连接FA,那么直线FA与⊙O相切吗?
25、(本小题满分10分)
某班到毕业时共结余经费1800元,班委会决定拿出不少于270元但不超过300元的资金为母校购买纪念品,其余资金用于在毕业晚会上给50位同学每人购买一件文化衫或一本相册作为纪念品.已知每件文化衫比每本相册贵9元,用200元恰好可以买到2件文化衫和5本相册.
(1)求每件文化衫和每本相册的价格分别为多少元?
(2)有几种购买文化衫和相册的方案?哪种方案用于购买老师纪念品的资金更充足?
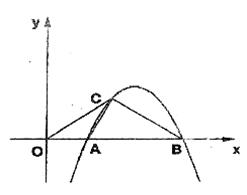
26.(本题满分l 2分)如图,抛物线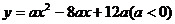 与
与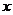 轴交于A、B两点(点A在点B的左侧),抛物线上另有一点C在第一象限,满足∠ACB为直角,且恰使△DCA∽△OBC.
轴交于A、B两点(点A在点B的左侧),抛物线上另有一点C在第一象限,满足∠ACB为直角,且恰使△DCA∽△OBC.
(1)球线段OC的长;
(2)求该抛物线的函数关系式;
(3)在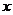 轴上是否存在点P,使△BCP为等腰三角形?若存在,求出所有符合条件的P点的坐标:若不存在,请说明理由.
轴上是否存在点P,使△BCP为等腰三角形?若存在,求出所有符合条件的P点的坐标:若不存在,请说明理由.