2008年北京市延庆县初三年级二模试卷
数学
一、选择题:
1.4的算术平方根是( )
A.2 B.-
2.在“迎奥运,全民健身”活动中,据不完全统计,截至
A.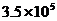 B.
B. C.
C.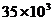 D.
D.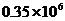
3.下列各式,运算正确的是( )
A.x2 ? x3=x6 B.x3-x2=x C.(-x)3(-x)=-x3 D.x6÷x2=x3
4.下列函数中,自变量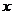 的取值范围是x>2的函数是( )
的取值范围是x>2的函数是( )
A.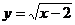 B.
B.  C.
C.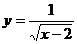 D.
D.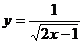
5. 王华五次数学考试成绩分别为:86分,78分,80分,85分,92分,李老师想了解他数学学习变化情况,则李老师应最关注王华数学成绩的( )
A.平均数 B.众数 C.中位数 D.方差
6.已知实数x,y满足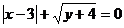 ,则代数式
,则代数式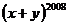 的值为( )
的值为( )
A.-1 B.
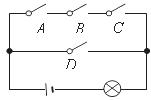
7.如图,电路图上有四个开关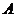 ,
, ,
,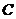 ,
,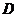 和一个小灯泡,闭合开关
和一个小灯泡,闭合开关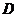 或同时闭合开关
或同时闭合开关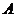 ,
, ,
,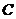 ,都可使小灯泡发光.任意闭合其中一个开关,则小灯泡发光的概率等于( )
,都可使小灯泡发光.任意闭合其中一个开关,则小灯泡发光的概率等于( )
A.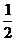 B.
B.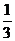 C.
C.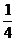 D.
D.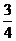
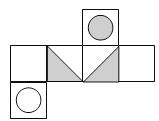
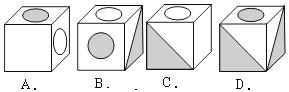
8.如图,是某一立方体的侧面展开图,则该立方体是( )
9.分解因式:ax2-6ax+9a= .
10. 已知关于x的方程x2+kx-3=0一个根是-2,则k的值为 .
11. 小王利用计算机设计了一个计算程序,输入和输出的数据如下表:当输入数据是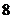 时,则输出的数据是 ;当输入数据是n时,则输出的数据是
时,则输出的数据是 ;当输入数据是n时,则输出的数据是
输入
…
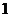
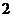
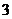
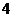
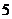
…
输出
…
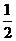
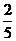

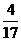
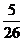
…
12.已知:如图, O为坐标原点,四边形OABC为矩形,A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 。
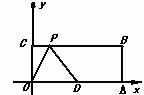
13. +(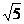 -1)0+()-1-3tan60°
-1)0+()-1-3tan60°
14. 解方程: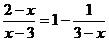
15.已知:如图4,BA=BD,BC=BE,∠ABD=∠CBE:
求证:AC=DE

16.已知:x2+x-1=0,求代数式的值: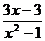 ?
?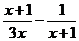
17. 已知:关于x的方程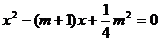
(1)当m取何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使得方程有两个不相等的整数根,并求出这两个根。
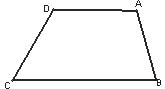
18. 已知:如图,梯形ABCD中,AD∥BC,∠ADC=120°,AD=5,CD=6,tanB=3,
求:梯形ABCD的面积。
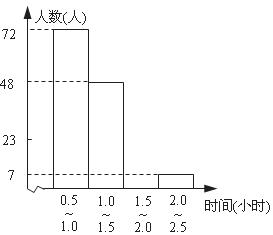
19. 我县初中校开展了“孝敬父母,从做家务事做起”的活动.为了解活动实施情况,专家组在22中随机抽取了七、八、九三个年级的学生共150名,调查他们一周(按七天计算)做家务所用的时间(单位:小时),得到一组数据,绘制成下表.请根据该表完成下列问题(说明0.5~1.0包括0.5,但不包括1.0,其余同理)
时间(单位:小时)
0.5~1.0
1.0~1.5
1.5~2.0
2.0~2.5
人 数
72
48
23
7
(1)根据上表的数据补全条形统计图;(2)写出这组数据的中位数落在什么范围内?
(3)根据以上信息判断,被调查的150名学生中,每周做家务所用的时间在1.5小时以下的学生所占的百分比是多少?
(4)若全县约有10000名初中生,请估计每周做家务所用的时间在1.5小时以下的学生人数.
(5)根据以上信息,请你提出一条积极合理的建议.
20. 已知:如图,以一底角为67.5°的等腰梯形ABCD的一腰BC为直径做⊙O,交底AB于E,且恰与另一腰AD相切于M;(1)求证:△EOM为等腰直角三角形;(2)求 的值.
的值.

21. 如图,边长为2的等边三角形OBA的顶点A在x轴的正半轴上,B点位于第一象限。将△OAB绕点O顺时针旋转30°后,得到△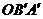 ,点
,点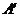 恰好落在双曲线
恰好落在双曲线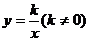 上.
上.
(1)在图中画出△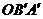 ;
;
(2)求双曲线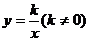 的解析式;
的解析式;
(3)等边三角形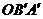 绕着点O继续按顺时针方向旋转 度后,
绕着点O继续按顺时针方向旋转 度后,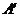 点再次落在双曲线上?(直接将答案填写在横线上即可,不需要说明理由)
点再次落在双曲线上?(直接将答案填写在横线上即可,不需要说明理由)
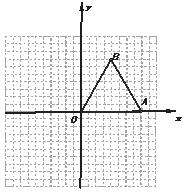
22. 在△ABC中,AB=AC,∠A=36°,把像这样的三角形叫做黄金三角形。
(1)请你设计三种不同的分法,将黄金三角形ABC分割成三个等腰三角形,使得分割成的三角形中含有两个黄金三角形(画图工具不限,要求画出分割线段;标出能够说明不同分法所得三角形的内角度数,不要求写画法,不要求证明.分别画在图1,图2,图3中)注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.(2)如图4中,BF平分∠ABC交AC于F,取AB的中点E,联结 EF并延长交 BC的延长线于M。试判断CM与AB之间的数量关系?只需说明结果,不用证明。
答:CM与AB之间的数量关系是 。
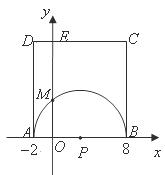
23. 如图,在平面直角坐标系中,A,B两点的坐标分别为A(-2,0),B(8,0),以AB为直径的半圆P与y轴交于点M,以AB为一边作正方形ABCD.
(1)求C,M两点的坐标;
(2)试判断直线CM与半圆P的位置关系,并证明你的结论。
(3)在x轴上是否存在一点Q,使得△QMC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
24.已知:抛物线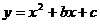 的对称轴是x=2,且经过点A(1,0),且与x轴的另一个交点为B,与y轴交于点C,
的对称轴是x=2,且经过点A(1,0),且与x轴的另一个交点为B,与y轴交于点C,
(1)确定此二次函数的解析式及顶点D的坐标;
(2)将直线CD沿y轴向下平移3个单位长度,求平移后直线m的解析式.
(3)在直线m上是否存在一点E,使得以点E、A、B、C为顶点的四边形是梯形,如果存在,求出满足条件的E点的坐标,如果不存在,说明理由。
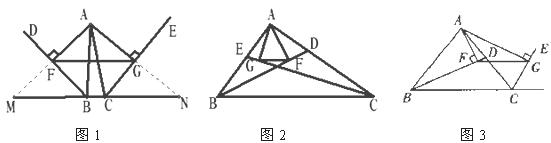
25.(本题满分8分)
(1)如图10-1所示,BD, CE分别是△ABC的外角平分线,过点A作AF⊥BD, AG⊥CE,垂足分别为F,G,连结FG,延长AF, AG,与直线BC分别交于点M、N,那么线段FG与△ABC的周长之间存在的数量关系是什么?即:FG= (AB+BC+AC) (直接写出结果即可)
(2)如图10-2,若BD,CE分别是△ABC的内角平分线;其他条件不变,线段FG与
ΔABC三边之间又有怎样的数量关系?请写出你的猜想,并给予证明.
(3)如图10-3,若BD为△ABC的内角平分线,CE为△ABC的外角平分线,其他条件不变,线段FG与ΔABC三边又有怎样的数量关系?直接写出你的猜想即可.不需要证明。
答:线段FG与ΔABC三边之间数量关系是 。