2008年泸州市初中毕业考试暨高中阶段学校招生统一考试
数学试卷
A卷
第Ⅰ卷 选择题(共39分)
一、选择题:本大题共13个小题,每小题3分,共39分. 在每小题给出的四个选项中,只有一个选项符合题意要求.
1.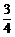 的的相反数是(
)
的的相反数是(
)
A.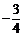 B.
B.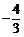 C.
C.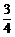 D.
D.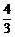
2.保护水资源,人人有责任,我国是缺水的国家,目前可利用的淡水资源的总量仅仅为899000亿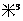 ,用科学计数法表示这个数是( )
,用科学计数法表示这个数是( )
A.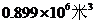 B.
B.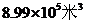 C.
C.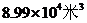 D.
D.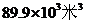
3.下列图形中,是轴对称图形的是( )

4.一组数据1,2,4,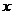 ,6的众数是2,则
,6的众数是2,则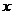 的值是( )
的值是( )
A.1 B.
5.在函数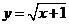 中,自变量
中,自变量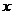 的取值范围是( )
的取值范围是( )
A.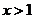 B.
B.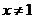 C.
C.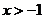 D.
D.
6.如图,正方形ABCD是⊙O的内接正方形,点P在劣弧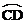 上不同于点C得到任意一点,则∠BPC的度数是( )
上不同于点C得到任意一点,则∠BPC的度数是( )
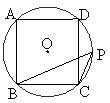
A.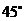 B.
B.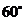 C.
C.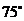 D.
D.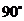
7.已知数据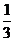 、
、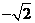 、
、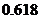 、125、
、125、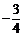 ,其中负数的概率为( )
,其中负数的概率为( )
A.20% B.40% C.60% D.80%
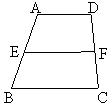
8.如图,梯形ABCD中,AD∥BC,E、F分别是两腰的中点,且AD=5,BC=7,则EF的长为( )
A.6 B.
9.下列图形中,不是正方形的表面展开图的是( )

10.不等式组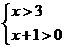 的解集是( )
的解集是( )
A.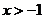 B.
B.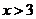 C.
C.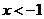 D.
D.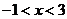
11.对于反比例函数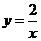 ,下列说法正确的是( )
,下列说法正确的是( )
A.点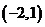 在它的图像上
在它的图像上
B.它的图像经过原点
C.它的图像在第一、三象限
D.当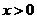 时,
时, 随
随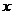 的增大而增大
的增大而增大
12.如图,PA切⊙O于A,PO交⊙O于B,若PA=6,PB=4,则⊙O的半径是( )
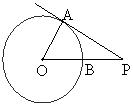
A.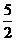 B.
B.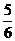 C.
C.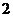 D.
D.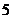
13.两个完全相同的长方体的长、宽、高分别是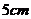 ,
,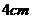 ,
,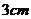 ,把它们按不同方式叠放在一起分别组成新的长方体,在这些新长方体中表面积最大的是( )
,把它们按不同方式叠放在一起分别组成新的长方体,在这些新长方体中表面积最大的是( )
A.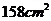 B.
B.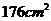 C.
C.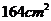 D.
D.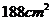
第Ⅱ卷 (非选择题 共61分)
二(本大题3个小题,共19分,⑴小题7分,⑵、⑶每小题6分)
14.⑴计算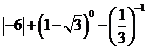
⑵分解因式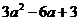
⑶化简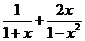
三(本大题2个小题,共16分,每小题8分)
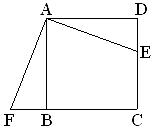
15.如图,E是正方形ABCD的边DC上的一点,过点A作FA⊥AE交CB的延长线于点F,求证:DE=BF
16.学习了统计知识后,小明的数学老师要求每个学生就本班同学的上学方式进行一次调查统计,如图是小明通过收集数据后绘制的两幅不完整的统计图。

请根据途中提供的信息,解答下列问题
⑴该班共有 名学生。
⑵将“骑自行车”部分的条形统计图补充完整;
⑶在扇形统计图中,求出“乘车”部分所对应的圆心角的度数;
⑷若全年级有600名学生,试估计该年级骑自行车上学的学生人数。
四、(本大题2个小题,共16分,每小题8分)
17.某乳制品厂,现有鲜牛奶10吨,若直接销售,每吨可获利500元;若制成酸奶销售,每吨可获利1200元;若制成奶粉销售,每吨可获利2000元,本工厂的生产能力是:若制成酸奶,每天可加工鲜牛奶3吨;若制成奶粉,每天可加工鲜牛奶1吨(两种加工方式不能同时进行)。受气温条件限制,这批鲜牛奶必须在4天内全部销售获加工完成。为此该厂设计了以下两种可行方案:
方案一:4天时间全部用来生产奶粉,其余直接销售鲜奶;
方案二:将一部分制成奶粉,其余制成鲜奶,并恰好4天完成。
你认为哪种方案获利最多,为什么?
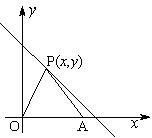
18.如图,在平面直角坐标系中,点P 是第一象限直线
是第一象限直线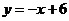 上的点,点A
上的点,点A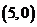 ,O是坐标原点,△PAO的面积为
,O是坐标原点,△PAO的面积为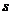
⑴求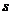 与
与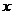 的函数关系式
的函数关系式
⑵当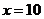 时,求
时,求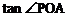 的值。
的值。
五(本大题10分)
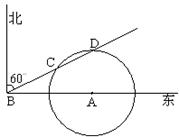
19.如图,在气象站台A的正西方向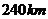 的B处有一台风中心,该台风中心以每小时
的B处有一台风中心,该台风中心以每小时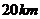 的速度沿北偏东
的速度沿北偏东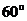 的BD方向移动,在距离台风中心
的BD方向移动,在距离台风中心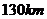 内的地方都要受到其影响。
内的地方都要受到其影响。
⑴台风中心在移动过程中,与气象台A的最短距离是多少?
⑵台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的实践会持续多长?
B卷
一、填空题(本大题5个小题,共40分,每小题4分)
1.若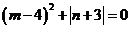 ,则
,则 ,
, 。
。
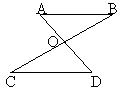
2.如图,AD与BC相较于O,AB∥CD,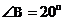 ,
,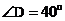 ,那么
,那么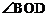 的度数为 。
的度数为 。
3.方程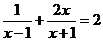 的解
的解 。
。
4.如图,两个同心圆的半径分别为2和1,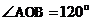 ,则阴影部分的面积为 。
,则阴影部分的面积为 。
5.已知关于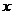 的一元二次方程
的一元二次方程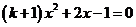 有两个不相同的实数根,则
有两个不相同的实数根,则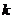 的取值范围是
。
的取值范围是
。
二、(本大题2个小题,共12分,每小题6分)
6.一个不透明的口袋里有红、黄、绿三种颜色的球(除颜色外其余都相同),其中红球有2个,黄球有1个,任意摸出一个黄球的概率为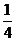 。
。
⑴试求口袋里绿球的个数。
⑵若第一次从口袋中任意摸出一球(不放回),第二次任意摸出一球,请你用树状图获列表法,求除两次都摸到红球的概率。
7.如图,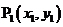 ,
,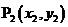 ,……
,……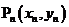 在函数
在函数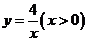 的图像上,
的图像上,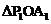 ,
,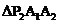 ,
,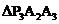 ,……
,……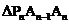 都是等腰直角三角形,斜边
都是等腰直角三角形,斜边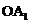 、
、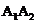 、
、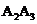 ,……
,……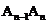 都在
都在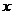 轴上。
轴上。
⑴求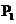 的坐标。
的坐标。
⑵求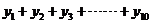 的值。
的值。

三、(本大题 8分)
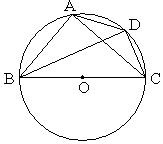
8.如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧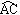 的中点,BD交AC于点E.⑴求证:
的中点,BD交AC于点E.⑴求证: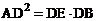 。
。
⑵若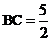 ,
,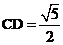 ,求DE的长。
,求DE的长。
四(本大题 10分)
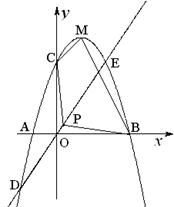
9.如图,已知二次函数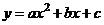 的图像经过三点A
的图像经过三点A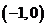 ,B
,B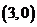 ,C
,C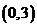 ,它的顶点为M,又正比例函数
,它的顶点为M,又正比例函数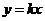 的图像于二次函数相交于两点D、E,且P是线段DE的中点。
的图像于二次函数相交于两点D、E,且P是线段DE的中点。
⑴求该二次函数的解析式,并求函数顶点M的坐标;
⑵已知点E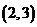 ,且二次函数的函数值大于正比例函数时,试根据函数图像求出符合条件的自变量
,且二次函数的函数值大于正比例函数时,试根据函数图像求出符合条件的自变量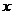 的取值范围;
的取值范围;
⑶当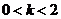 时,求四边形PCMB的面积
时,求四边形PCMB的面积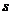 的最小值。
的最小值。
【参考公式:已知两点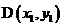 ,
,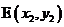 ,则线段DE的中点坐标为
,则线段DE的中点坐标为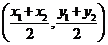 】
】