2008年荆州市初中升学考试
数学试卷
第Ⅰ卷(选择题和填空题,共42分)
一、选择题(每小题3分,共24分)
1.下列根式中属最简二次根式的是( )
A. B.
B.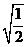 C.
C.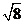 D.
D.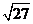
2.我国第一颗探月卫星“嫦娥一号”从环月轨道传回第一张月面照片时距地球38万公里.将38万公里科学记数法表示应为( )
A.38×104 B.3.8×
3.将一直角三角板与两边平行的纸条如图所示放置,下列结论:(1)∠1=∠2;(2)∠3=∠4;(3)∠2+∠4=90°;(4)∠4+∠5=180°,其中正确的个数是( )

A.1 B
4.方程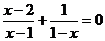 的解是( )
的解是( )
A.2 B
5.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,O为位似中心,
OD=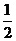 OD′,则A′B′:AB为( )
OD′,则A′B′:AB为( )
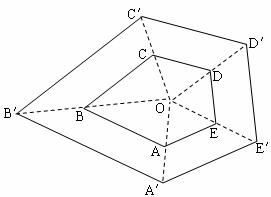
A.2:3 B.3:
6.甲、乙、丙三家超市为了促销一种定价均为m元的商品,甲超市连续两次降价20%,乙超市一次性降价40%,丙超市第一次降价30%,第二次降价10%,此时顾客要购买这种商品最划算应到的超市是 ( )
A.甲 B.乙 C.丙 D. 乙或丙
7.如图,在平面直角坐标系中,点A在第一象限,⊙A与轴相切于B,与轴交于C(0,1),D(0,4)两点,则点A的坐标是 ( )

A. B.
B.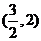 C.
C.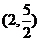 D.
D.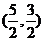
8.如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为 ( )

A.5:3 B.3:
二、填空题(每小题3分,共18分)
9.计算: __________________.
__________________.
10.两个相似三角形周长的比为2:3,则其对应的面积比为___________.
11.在如图所示的8×8正方形网格纸板上进行投针实验,随意向纸板投中一针,投中阴影部分的概率是___________.

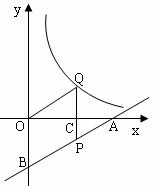
12.如图,一次函数 的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数
的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数 的图象于Q,
的图象于Q, ,则k的值和Q点的坐标分别为_________________________.
,则k的值和Q点的坐标分别为_________________________.
13.关于的方程 两实根之和为m,且满足
两实根之和为m,且满足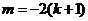 ,关于y的不等于组
,关于y的不等于组 有实数解,则k的取值范围是______________________.
有实数解,则k的取值范围是______________________.
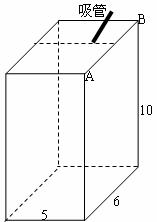
14.如图所示的长方体是某种饮料的纸质包装盒,规格为5×6×10(单位:┩),在上盖中开有一孔便于插吸管,吸管长为13┩, 小孔到图中边AB距离为1┩,到上盖中与AB相邻的两边距离相等,设插入吸管后露在盒外面的管长为h┩,则h的最小值大约为_________┩.(精确到个位,参考数据: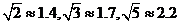 )
)
第Ⅱ卷(非选择题,共78分)
15.(本题5分)已知a为实数,求代数式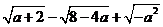 的值.
的值.
16.(本题5分)解方程组
17.(本题5分)已知点P(a+1,
18.(本题6分)正方形绿化场地拟种植两种不同颜色的花卉,要求种植的花卉能组成轴对称或中心对称图案.下面是三种不同设计方案中的一部分,请把图①、图②补成既是轴对称图形,又是中心对称图形,并画出一条对称轴;把图③补成只是中心对称图形,并把中心标上字母P.(在你所设计的图案中用阴影部分和非阴影部分表示两种不同颜色的花卉.)

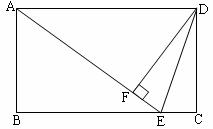
19.(本题6分)如图,矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE于F,连结DE,求证:DF=DC.
20.(本题6分)已知:如图,Rt△AOB的两直角边OA、OB分别在x轴的正半轴和y轴的负半轴上,C为OA上一点且OC=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常 数且m+2≥2p>0)经过A、C两点.
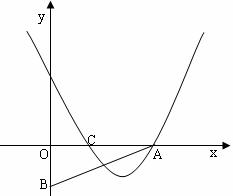
(1)用m、p分别表示OA、OC的长;
(2)当m、p满足什么关系时,△AOB的面积最大.
21.(本题7分)已知:如图,AB是⊙O的切线,切点为A,OB交⊙O于C且C为OB中点,过C点的弦CD使∠ACD=45°, 的长为
的长为 ,求弦AD、AC的长.
,求弦AD、AC的长.

22.(本题8分)为了节约资源,保护环境,从
(1)本次抽样的样本容量是________________.
(2)图中a=___________(户),c=___________(户).
(3)若被调查的家庭占全城区家庭数的10%,请估计该城区不再使用超薄塑料袋的家庭数.
(4)针对本次调查结果,请用一句话发表你的感想.

23.(本题8分)载着“点燃激情,传递梦想”的使用, )
)
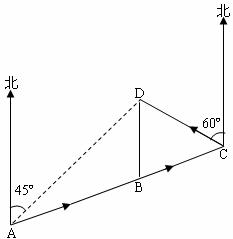
24.(本题10分)“5•

(1)求y1与x的函数解析式;
(2)求五月份该公司的总销售量;
(3)设公司五月份售出甲种型号器材t台,五月份总销售利润为W(万元),求W与t的函数关系式;(销售利润=销售额-进价-其他各项支出)
(4)请推测该公司这次向灾区捐款金额的最大值.
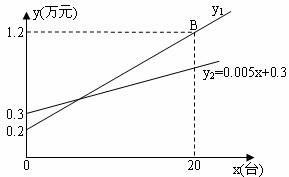
25.(本题12分)如图,等腰直角三角形纸片ABC中,AC=BC=4,∠ACB=90º,直角边AC在x轴上,B点在第二象限,A(1,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在直线重合,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA平移,至B点到达A点停止.设平移时间为t(s),移动速度为每秒1个单位长度,平移中四边形BCFE与△AEF重叠的面积为S.
(1)求折痕EF的长;
(2)是否存在某一时刻t使平移中直角顶点C经过抛物线 的顶点?若存在,求出t值;若不存在,请说明理由;
的顶点?若存在,求出t值;若不存在,请说明理由;
(3)直接写出S与t的函数关系式及自变量t的取值范围.