2008年宁夏回族自治区初中毕业暨高中阶段招生
数学试卷
一、选择题(下列每小题所给的四个答案中只有一个是正确的,每小题3分,共24分)
1.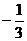 的绝对值是( )
的绝对值是( )
A. -3
B. 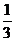 C. 3
D.
C. 3
D. 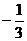
2.根据国务院抗震救灾总指挥部权威发布:截止
A. 4.5502×10 元 B. 4.5502×10
元 B. 4.5502×10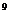 元
元
C. 4.5502×10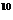 元 D. 4.5502×10
元 D. 4.5502×10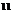 元
元
3.下列各式运算正确的是( )
A.2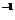 =
=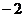 B.2
B.2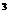 =
=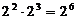 D.
D.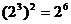
4.下列分解因式正确的是( )
A.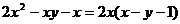 B.
B.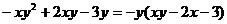
C.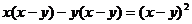 D.
D.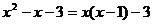
5.甲、乙两名学生10次立定跳远成绩的平均数相同,若甲10次立定跳远成绩的方差S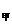
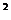 =0.006,乙10次立定跳远成绩的方差S
=0.006,乙10次立定跳远成绩的方差S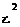 =0.035,则( )
=0.035,则( )
A.甲的成绩比乙的成绩稳定 B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定 D.甲、乙两人成绩的稳定性不能比较
6.平行四边形ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )
A. AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD
7.反比例函数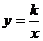 (k>0)的部分图象如图所示,A、B是图象上两点,AC⊥
(k>0)的部分图象如图所示,A、B是图象上两点,AC⊥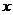 轴于点C,BD⊥
轴于点C,BD⊥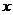 轴于点D,若△AOC的面积为S
轴于点D,若△AOC的面积为S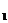 ,△BOD的面积为S
,△BOD的面积为S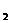 ,则S
,则S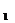 和S
和S 的大小关系为( )
的大小关系为( )
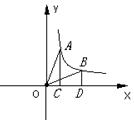
A.S > S
> S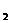 B.S
B.S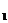 = S
= S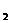 C.S
C.S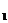 <S
<S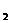 D.无法确定
D.无法确定
8.已知⊙O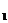 和⊙O
和⊙O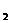 相切,两圆的圆心距为
相切,两圆的圆心距为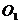 的半径为
的半径为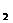 的半径为( )
的半径为( )
A.
二、填空题(每小题3分,共24分)
9.计算: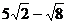 = .
= .
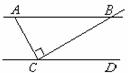
10. 如图,AB∥CD, AC⊥BC,∠BAC =65°,则∠BCD= 度.
11.某市对一段全长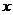 米,为了尽量减少施工对城市交通所造成的影响,实际施工时,每天修路比原计划的2倍还多
米,为了尽量减少施工对城市交通所造成的影响,实际施工时,每天修路比原计划的2倍还多
12.学校为七年级学生订做校服,校服型号有小号、中号、大号、特大号四种.随机抽取了100名学生调查他们的身高,得到身高频数分布表如下:
型 号
身高(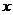 /cm)
/cm)
人 数(频数)
小 号
145≤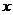 <155
<155
22
中 号
155≤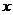 <165
<165
45
大 号
165≤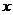 <175
<175
28
特大号
175≤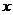 <185
<185
5
已知该校七年级学生有800名,那么中号校服应订制 套.
13.从-1,1,2三个数中任取一个,作为一次函数y=k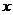 +3的k值,则所得一次函数中
+3的k值,则所得一次函数中 随
随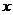 的增大而增大的概率是 .
的增大而增大的概率是 .
14.制作一个圆锥模型,已知圆锥底面圆的半径为
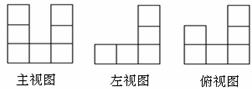
15. 展览厅内要用相同的正方体木块搭成一个三视图如右图的展台,则此展台共需这样的
正方体______块.
16. 已知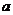 、b、c为三个正整数,如果
、b、c为三个正整数,如果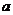 +b+c=12,那么以
+b+c=12,那么以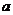 、b、c为边能组成的三角形是:①等腰三角形;②等边三角形;③直角三角形;④钝角三角形.以上符合条件的正确结论是
.(只填序号)
、b、c为边能组成的三角形是:①等腰三角形;②等边三角形;③直角三角形;④钝角三角形.以上符合条件的正确结论是
.(只填序号)
三、解答题(共24分)
17.(6分)
先化简,再求值: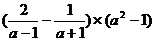 ,其中
,其中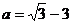 .
.
18.(6分)
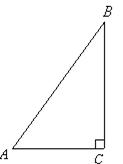
如图,在△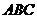 中,∠
中,∠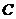 =90°,sin
=90°,sin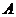 =
=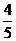 ,
,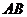 =15,求△
=15,求△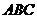 的周长和tan
的周长和tan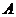 的值.
的值.
19.(6分)
汶川地震牵动着全国亿万人民的心,某校为地震灾区开展了“献出我们的爱” 赈灾捐款活动.八年级(1)班50名同学积极参加了这次赈灾捐款活动,下表是小明对全班捐款情况的统计表:

因不慎两处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数、中位数分别是多少?
20. (6分)
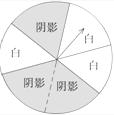
张红和王伟为了争取到一张观看奥运知识竞赛的入场券,他们各自设计了一个方案:
张红的方案是:转动如图所示的转盘,如果指针停在阴影区域,则张红得到入场券;如果指针停在白色区域,则王伟得到入场券(转盘被等分成6个扇形.若指针停在边界处,则重新转动转盘).
王伟的方案是:从一副扑克牌中取出方块1、2、3,将它们背面朝上重新洗牌后,从中摸出一张,记录下牌面数字后放回,洗匀后再摸出一张.若摸出两张牌面数字之和为奇数,则张红得到入场?;若摸出两张牌面数字之和为偶数,则王伟得到入场券.
(1)计算张红获得入场券的概率,并说明张红的方案是否公平?
(2)用树状图(或列表法)列举王伟设计方案的所有情况,
计算王伟获得入场券的概率,并说明王伟的方案是否公平?
四、解答题(共48分)
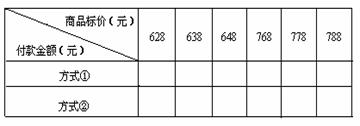
21.(6分)
商场为了促销,推出两种促销方式:
方式①:所有商品打7.5折销售:
方式②:一次购物满200元送60元现金.
(1)
方案一:628元和788元的商品均按促销方式①购买;
方案二:628元的商品按促销方式①购买,788元的商品按促销方式②购买;
方案三:628元的商品按促销方式②购买,788元的商品按促销方式①购买;
方案四:628元和788元的商品均按促销方式②购买.
你给杨老师提出的最合理购买方案是 .
 (2)通过计算下表中标价在600元到800元之间商品的付款金额,你总结出商品的购买规律是
.
(2)通过计算下表中标价在600元到800元之间商品的付款金额,你总结出商品的购买规律是
.
22.(6分)
如图,在边长均为1的小正方形网格纸中,△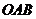 的顶点
的顶点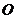 、
、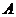 、
、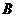 均在格点上,且
均在格点上,且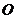 是直角坐标系的原点,点
是直角坐标系的原点,点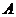 在
在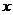 轴上.
轴上.
(1)以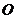 为位似中心,将△
为位似中心,将△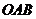 放大,使得放大后的△
放大,使得放大后的△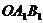 与△
与△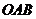 对应线段的比为2∶1,画出△
对应线段的比为2∶1,画出△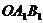 .(所画△
.(所画△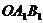 与△
与△ 在原点两侧).
在原点两侧).
(2)求出线段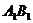 所在直线的函数关系式.
所在直线的函数关系式.
23.(8分)
已知二次函数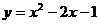 .
.
(1)
求此二次函数的图象与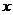 轴的交点坐标.
轴的交点坐标.
(2)二次函数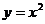 的图象如图所示,将
的图象如图所示,将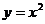 的图象经过怎样的平移,就可以得到二次函数
的图象经过怎样的平移,就可以得到二次函数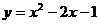 的图象.
的图象.
(参考:二次函数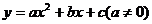 图象的顶点坐标是(
图象的顶点坐标是(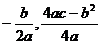 ))
))

24.(8分)
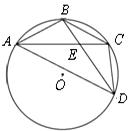
如图,梯形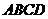 内接于⊙
内接于⊙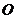 ,
,  ∥
∥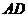 ,
,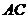 与
与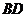 相交于点
相交于点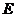 ,在不添加任何辅助线的情况下:
,在不添加任何辅助线的情况下:
(1) 图中共有几对全等三角形,请把它们一一写出来,并选择其中一对全等三角形进行证明.
(2)
若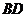 平分∠
平分∠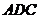 ,请找出图中与△
,请找出图中与△ 相似的所有三角形.
相似的所有三角形.
25.(10分)
为极大地满足人民生活的需求,丰富市场供应,我区农村温棚设施农业迅速发展,温棚种植面积在不断扩大.在耕地上培成一行一行的矩形土埂,按顺序间隔种植不同农作物的方法叫分垄间隔套种.科学研究表明:在塑料温棚中分垄间隔套种高、矮不同的蔬菜和水果(同一种紧挨在一起种植不超过两垄),可增加它们的光合作用,提高单位面积的产量和经济效益.
现有一个种植总面积为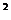 的矩形塑料温棚,分垄间隔套种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物的总垄数不低于10垄,又不超过14垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
的矩形塑料温棚,分垄间隔套种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物的总垄数不低于10垄,又不超过14垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
占地面积(m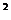 /垄)
/垄)
产量(千克/垄)
利润(元/千克)
西红柿
30
160
1.1
草莓
15
50
1.6
(1)若设草莓共种植了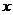 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种?
(2)在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
26. (10分)
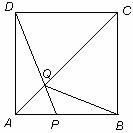
如图,在边长为4的正方形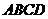 中,点
中,点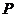 在
在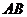 上从
上从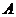 向
向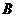 运动,连接
运动,连接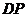 交
交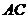 于点
于点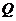 .
.
(1)试证明:无论点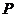 运动到
运动到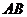 上何处时,都有△
上何处时,都有△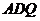 ≌△
≌△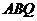 ;
;
(2)当点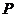 在
在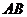 上运动到什么位置时,△
上运动到什么位置时,△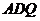 的面积是正方形
的面积是正方形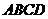 面积的
面积的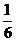 ;
;
(3)若点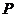 从点
从点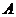 运动到点
运动到点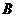 ,再继续在
,再继续在 上运动到点
上运动到点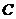 ,在整个运动过程中,当点
,在整个运动过程中,当点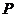 运动到什么位置时,△
运动到什么位置时,△ 恰为等腰三角形.
恰为等腰三角形.