2008年北京市朝阳区初三年级二模试卷 数学
一、选择题:
1.2的算术平方根是( )
A.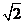 B.
B.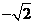 C.
C.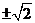 D.
D.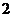
2.下列运算中,正确的是( )
A.x2?x3=x6 B.2-1= 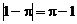 D.
D.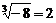
3.为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是 ( )
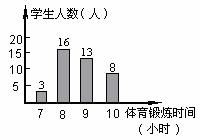
A.8,9 B.8,
4.如果关于x的方程 kx2 -2x -1=0有两个实数根,那么k的取值范围是( )
A.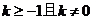 B.
B.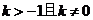 C.
C.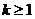 D.
D.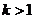
5.不等式组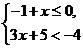 的解集在数轴上可表示为 ( )
的解集在数轴上可表示为 ( )
A.x≤0 B.-3<x≤
6.小华想做一个边长是
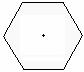
A.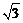 cm
D.10
cm
D.10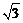 cm
cm
7.如图,从点P向⊙O引两条切线PA,PB,切点为A,B,BC为⊙O的直径,若∠P=60°,PA=3,则⊙O的直径BC的长为 ( )
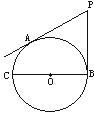
A.3
B.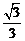 C.2
C.2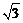 D.4
D.4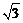
8.一个等边三角形的边长为2,分别以它的三个顶点为圆心,边长为半径画弧,得到下图,那么图中所有的弧长的和是( )
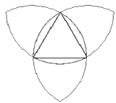
A.4π B.6π C.8π D.10π
9.计算:cos60°-π0=________.
10.已知两圆的半径分别为3┩和4┩,如果这两个圆的圆心距为10┩,那么这两个圆_____.
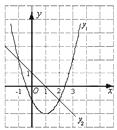
11.在正方形的网格中,抛物线y1=x2+bx+c与直线y2=kx+m的图象如图所示,请你观察图象并回答:当-1<x<2时,y1____y2(填“>”或“<”或“=”号).
12.我们把分子为1的分数叫做理想分数,如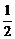 ,
,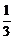 ,
,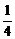 ,… ,任何一个理想分数都可以写成两个不同理想分数的和,如
,… ,任何一个理想分数都可以写成两个不同理想分数的和,如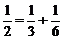 ;
; 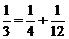 ;
; 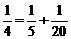 ; …根据对上述式子的观察,请你思考:如果理想分数
; …根据对上述式子的观察,请你思考:如果理想分数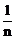 (n是不小于2的正整数)=
(n是不小于2的正整数)=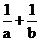 ,那么a+b= .(用含n的式子表示)
,那么a+b= .(用含n的式子表示)
13.解方程组 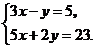
14. 化简: 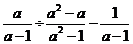 .
.
15.用配方法解方程 x2 -6x+1=0.
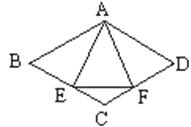
16.已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.
求证:∠AEF=∠AFE.
17.欢欢的妈妈有粉色、米色和天蓝色三条丝绸围巾,有红色和黑色三件羊绒衫(其中红色一件、黑色两件).如果她最喜欢的搭配是米色围巾和黑色羊绒衫,那么黑暗中她随机拿出一条围巾和一件羊绒衫,正好是她喜欢搭配的颜色.请你用树形图或列表法,求出这样的巧合发生的概率?
捐款(单位:元)
20
50
100
150
200
人数
4
12
9
3
2
18.自从2008年5月12日我国四川地区发生特大地震以来,全国人民“众志成城 抗震救灾”,纷纷捐款献爱心,在某校的一次捐款活动中,九年级(1)班30名学生捐款情况如下表:
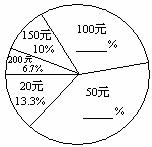
求(1)该班平均每人捐款多少元?
(2)补全右图所示的捐款人数比例的扇形统计图;
(3)请你根据以上信息发表自己的一个见解.
19.某社区为迎接绿色奥运,大力开展社区绿化建设,购买了甲、乙两种树苗共400株,其中甲种树苗每株60元,乙种树苗每株90元(1)如果购买这批树苗一共用了29400元,那么甲、乙两种树苗各购买了多少株?
(2)如果社区准备再次购买这两种树苗,不仅要使甲种树苗的数量是乙种树苗数量的二倍,而且要使所需费用不多于14700元,那么甲种树苗最多买多少株?
20. 如图线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.(1)请你在所给的网格中画出线段AC;(2)判断将线段AB旋转到线段AC的过程中,线段AB扫过的区域所形成的图形是哪个立体图形的侧面展开图?将答案直接填写在后面的横线上_________; (3)求出(2)中所说立体图形的侧面展开图的面积.
21.如图,点C在反比例函数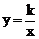 的图象上,过点C作CD⊥y轴,交y轴负半轴于点D,且△ODC的面积是3.
的图象上,过点C作CD⊥y轴,交y轴负半轴于点D,且△ODC的面积是3.
(1)求反比例函数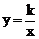 的解析式;
的解析式;
(2)将过点O且与OC所在直线关于y轴对称的直线向上平移2个单位后得到直线AB,如果CD=1,求直线AB的解析式.
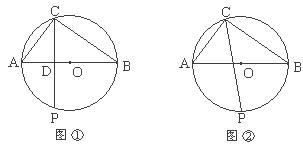
22.已知:如图,AB为⊙O的直径,AC、BC为弦,点P为 上一点,AB=10,AC∶BC=3∶4.
上一点,AB=10,AC∶BC=3∶4.
(1)当点P与点C关于直线AB对称时(如图①),求PC长;
(2)当点P为 的中点时(如图②),求PC长.
的中点时(如图②),求PC长.
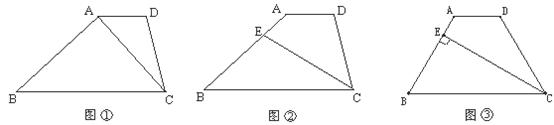
23.已知:如图,在梯形ABCD中,AD∥BC,BC=3AD.
(1)如图①,连接AC,如果三角形ADC的面积为6,求梯形ABCD的面积;
(2)如图②,E是腰AB上一点,连结CE,设△BCE和四边形AECD的面积分别为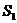 和
和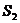 ,且
,且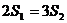 ,求
,求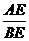 的值;
的值;
(3)如图③,AB=CD,如果CE⊥AB于点E,且BE=3AE,求∠B的度数.
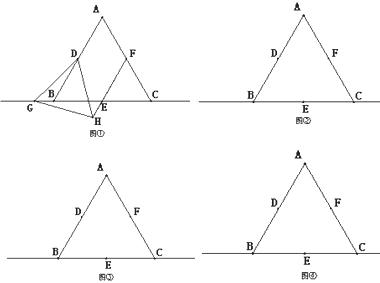
24.已知:在等边△ABC中,点D、E、F分别为边AB、BC、AC的中点,点G为直线BC上一动点,当点G在CB延长线上时,有结论“在直线EF上存在一点H,使得△DGH 是等边三角形”成立(如图①),且当点G与点B、E、C重合时,该结论也一定成立.问题:当点G在直线BC的其它位置时,该结论是否仍然成立?请你在下面的备用图②③④中,画出相应图形并证明相关结论.
25.如图,△AOC在平面直角坐标系中,∠AOC=90°,且O为坐标原点,点A、C分别在坐标轴上,AO=4,OC=3,将△AOC绕点C按逆时针方向旋转,旋转后的三角形记为△CA′O′.当CA边落在y轴上(其中旋转角为锐角)时,一条抛物线经过A、C两点且与直线AA′ 相交于x轴下方一点D,如果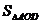 =9,求这条抛物线的解析式;继续旋转△CA′O′,当以CA′为直径的⊙P与(1)中抛物线的对称轴相切时,圆心P是否在抛物线上,请说明理由.
=9,求这条抛物线的解析式;继续旋转△CA′O′,当以CA′为直径的⊙P与(1)中抛物线的对称轴相切时,圆心P是否在抛物线上,请说明理由. 
