2008年常州市初中毕业、升学统一考试
数学试卷
一、填空题:
1.-3的相反数是_______,- 的绝对值是________,2-1=______.
的绝对值是________,2-1=______.
2.点A(-2,1)关于y轴对称的点的坐标为___________,关于原点对称的点的坐标为________.
3.如图,在△ABC中BE平分∠ABC,DE∥BC,∠ABE=35°,则∠DEB=______°,
∠ADE=_____°.
4.已知一组数据为5,6,8,6,8,8,8,则这组数据的众数是_________,平均数是_________.
5.已知扇形的半径为
 6.过反比例函数
6.过反比例函数 的图象上的一点分别作x、y轴的垂线段,如果垂线段与x、y轴所围成的矩形面积是6,那么该函数的表达式是______;若点A(-3,m)在这个反比例函数的图象上,则m=______.
的图象上的一点分别作x、y轴的垂线段,如果垂线段与x、y轴所围成的矩形面积是6,那么该函数的表达式是______;若点A(-3,m)在这个反比例函数的图象上,则m=______.
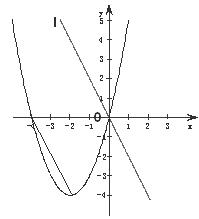
7.已知函数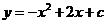 的部分图象如图所示,则c=______,当x______时,y随x的增大而减小.
的部分图象如图所示,则c=______,当x______时,y随x的增大而减小.

8.若将棱长为2的正方体切成8个棱长为1的小正方体,则所有小正方体的表面积的和是原正方体表面积的_______倍; 若将棱长为3的正方体切成27个棱长为1的小正方体,则所有小正方体的表面积的和是原正方体表面积的_______倍; 若将棱长为n(n>1,且为整数)的正方体切成n3个棱长为1的小正方体,则所有小正方体的表面积的和是原正方体表面积的_______倍.
二、选择题:
9.下列实数中,无理数是( )
A.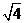 B.
B.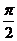 C.
C.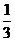 D.
D.
10.若式子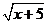 在实数范围内有意义,则x的取值范围是 ( )
在实数范围内有意义,则x的取值范围是 ( )
A.x>-5 B.x<
11.若反比例函数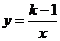 的图象在其每个象限内,y随x的增大而减小,则k的值可以是(
)
的图象在其每个象限内,y随x的增大而减小,则k的值可以是(
)
A.-1 B.3 C.0 D.-3
12.在体育课上,九年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生立定跳远成绩的( )
A.方差 B.平均数 C.频率分布 D.众数
13.顺次连接菱形各边中点所得的四边形一定是( )
A.等腰梯形 B.正方形 C.平行四边形 D.矩形
14.如图,它需再添一个面,折叠后才能围成一个正方体,下图中的黑色小正方形分别由四位同学补画,其中正确的是 ( )


15.如图,在△ABC中,若DE∥BC, =
= ,DE=4cm,则BC的长为 ( )
,DE=4cm,则BC的长为 ( )

A.8cm B.12cm C.11cm D.10cm
16.如图,若⊙的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且⊙O的半径为2,则CD的长为 ( )

A. B.
B. C.2 D. 4
C.2 D. 4
17甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和骑行时间t(h)之间的函数关系如图所示,给出下列说法: ( )
(1)他们都骑行了20km;
(2)乙在途中停留了0.5h;
(3)甲、乙两人同时到达目的地;
(4)相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有

A.1个 B.2个 C.3个 D.4个
(本小题满分10分)化简:
三.解答题(本大题共2小题,共18分,解答时应写出演算步骤)
18.(1)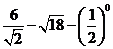 (2)
(2)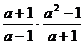
19.(本小题满分8分)解方程(组)
(1)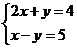 (2)
(2)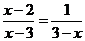
四.解答题(本大题共2小题,共12分,解答时应写出文字说明或演算步骤)
20.(本小题满分6分)
为了解九年级女生的身高(单位:cm)情况,某中学对部分九年级女生身高进行了一次测量 , 所得数据整理后列出了频数分布表,并画了部分频数分布直方图(图、表如下):
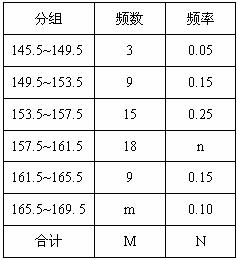
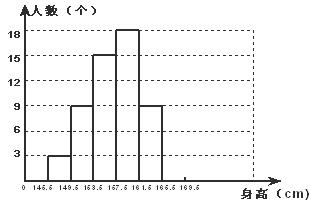
根据以上图表,回答下列问题:
(1)M=_______,m=_______,N=_______,n=__________;
(2)补全频数分布直方图.
21.(本小题满分6分)
小敏和小李都想去看我市举行的乒乓球比赛,但俩人只有一张门票.小敏建议通过摸球来决定谁去欣赏,他的方法是:把1个白球和2个红球放在一只不透明的袋子中(这些球除颜色外都相同,搅匀后从中任意摸出1个球,记录下颜色后放袋中并搅匀,再从中任意摸出1个球.如果两次都摸出相同颜色的球,则小敏自己去看比赛,否则小李去看比赛.问小敏的这个方法对双方公平吗?请说明理由.
五.解答题(本大题共2小题,共14分,解答时应写出证明过程)
22.(本小题满分7分)
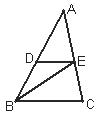
已知:如图,AB=AD,AC=AE,∠BAD=∠CAE.求证:AC=DE.
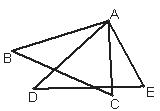
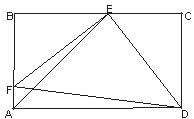
23.已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.
求证:AE平分∠BAD.
六.画图与探究(本大题共2小题,共14分)
24.(本小题满分6分)
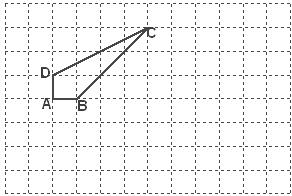
已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD的顶点都在格点上.
(1)在所给网格中按下列要求画图:
① 在网格中建立平面直角坐标系(坐标原点为O),使四边形ABCD各个顶点的坐标分别为A(-5,0)、B(-4,0)、C(-1,3),D(-5,1);
② 将四边形ABCD沿坐标横轴翻折180°,得到四边形A’B’C’D’,再将四边形A’B’C’D’绕原点O旋转180°,得到四边形A”B”C”D”;
(2)写出C”、D”的坐标;
(3)请判断四边形A”B”C”D”与四边形ABCD成何种对称?若成中心对称,请写出对称中心;若成轴对称,请写出对称轴.
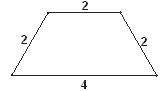
25.如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.
七.解答题(本大题共3小题,共26分,解答时应写出文字说明、证明过程或演算步骤) (本小题满分8分)
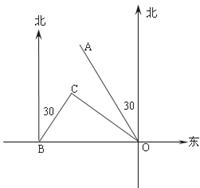
26.如图,港口B位于港口O正西方向120海里外,小岛C位于港口O北偏西60°的方向.一艘科学考察船从港口O出发,沿北偏东30°的OA方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B出发,沿北偏东30°的方向以60海里/小时的速度驶向小岛C,在小岛C用1小时装补给物资后,立即按原来的速度给考察船送去.
(1) 快艇从港口B到小岛C需要多少时间?
(2) 快艇从小岛C出发后最少需要多少时间才能和考察船相遇?
27.(本小题满分7分)
2008年5月12日四川汶川地区发生8.0级特大地震.举国上下通过各种方式表达爱心.某企业决定用p万元援助灾区n所学校,用于搭建帐篷和添置教学设备.根据各校不同的受灾情况,该企业捐款的分配方案是:所有学校得到的捐款数都相等,到第n所学校的捐款恰好分完,捐款的分配方法如下表所示.(其中p,n,a都是正整数)
分配顺序
分配数额(单位:万元)
帐篷费用
教学设备费用
第1所学校
5
剩余款的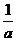
第2所学校
10
剩余款的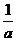
第3所学校
15
剩余款的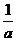
…
…
…
第(n-1)所学校
5(n-1)
剩余款的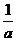
第n所学校
5n
0
根据以上信息,解答下列问题:
(1)写出p与n的关系式;
(2)当p=125时,该企业能援助多少所学校?
(3)根据震区灾情,该企业计划再次提供不超过20a万元的捐款,按照原来的分配方案援助其它学校.若a由 (2)确定,则再次提供的捐款最多又可以援助多少所学校?
28.如图,抛物线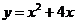 与x轴分别相交于点B、O,它的顶点为A,连接AB,把AB所的直线沿y轴向上平移,使它经过原点O,得到直线l,设P是直线l上一动点.
与x轴分别相交于点B、O,它的顶点为A,连接AB,把AB所的直线沿y轴向上平移,使它经过原点O,得到直线l,设P是直线l上一动点.
(1)求点A的坐标;
(2)以点A、B、O、P为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P的坐标;
(3)设以点A、B、O、P为顶点的四边形的面积为S,点P的横坐标为x,当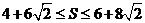 时,求x的取值范围.
时,求x的取值范围.