2007-2008学年度莱州市第一学期初四期中考试
数学试题
一、填空题(每题3分,共30分)
1.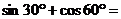 。
。
2.在Rt△ABC中,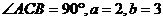 ,则
,则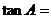 。
。
3.已知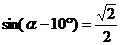 ,则锐角
,则锐角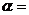 。
。
4.一种汽车爬坡的最大能力是倾斜角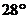 。若一段坡的坡比是1┱
。若一段坡的坡比是1┱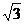 ,这辆汽车 爬过此坡(填“能”或“不能”)。
,这辆汽车 爬过此坡(填“能”或“不能”)。
5.当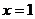 时,函数
时,函数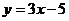 的函数值等于 。
的函数值等于 。
6.写出一个对称轴是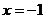 的二次函数表达式 。
的二次函数表达式 。
7.抛物线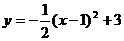 的顶点坐标是 。
的顶点坐标是 。
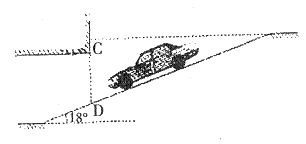
8.如图,CD为地下停车库的入口。按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入。已知 米,则在C点上方张贴的限高约为 米(精确到
米,则在C点上方张贴的限高约为 米(精确到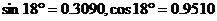 )。
)。
9.已知二次函数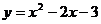 的图像与
的图像与 轴交于A、B两点,点C是抛物线上异于A、B的一个点,当△ABC的面积等于 时,满足条件的点C有且只有三个。
轴交于A、B两点,点C是抛物线上异于A、B的一个点,当△ABC的面积等于 时,满足条件的点C有且只有三个。
10.小明发现横在教学楼走廊上一拖把,此拖把以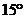 的倾斜角斜靠在墙壁上,影响了同学们的行走安全。他自觉地将拖把挪动位置,使它的倾斜角为
的倾斜角斜靠在墙壁上,影响了同学们的行走安全。他自觉地将拖把挪动位置,使它的倾斜角为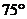 。如果拖把的总长为
。如果拖把的总长为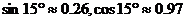 )。
)。
二、选择题(每小题3分,共30分)
11.将Rt△ABC的斜边和一直角边都扩大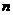 倍,那么锐角A的三角函数值
倍,那么锐角A的三角函数值
A.都扩大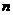 倍 B.都缩小
倍 B.都缩小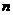 倍
倍
C.没有变化 D.只有tanA发生变化
12.下列三角函数值最大的是
A.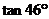 B.
B.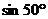 C.
C.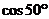 D.
D.
13.将抛物线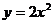 向右平移2个单位,能得到的抛物线是
向右平移2个单位,能得到的抛物线是
A.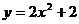 B.
B.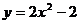
C.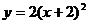 D.
D.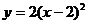
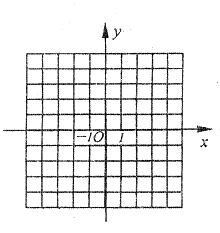
14.已知二次函数的图像如图所示,那么此函数的解析式可能是
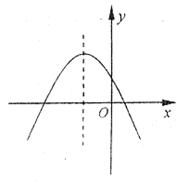
A.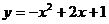 B.
B.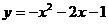
C.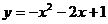 D.
D.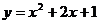
15.抛物线 开口向下,与
开口向下,与 轴两个交点的横坐标分别为
轴两个交点的横坐标分别为 和
和 ,则下列结论正确的是
,则下列结论正确的是
A. B.
B.
C. D.
D.
16.已知:二次函数 (
( 为大于0的常数),当
为大于0的常数),当 时的函数值
时的函数值 ;则当
;则当 时的函数值
时的函数值 与0的大小关系为
与0的大小关系为
A. B.
B. C.
C. D.不能确定
D.不能确定
17.抛物线 的顶点在第三象限,且
的顶点在第三象限,且 ,则关于此抛物线的说法正确的是
,则关于此抛物线的说法正确的是
A.抛物线的开口向上,与 轴交于正半轴
轴交于正半轴
B.抛物线的开口向上,与 轴交于负半轴
轴交于负半轴
C.抛物线的开口向下,与 轴交于正半轴
轴交于正半轴
D.抛物线的开口向下,与 轴交于负半轴
轴交于负半轴
18.在Rt△ABC中,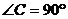 。若sinA┱tanA
。若sinA┱tanA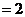 ┱
┱ ,则cosA等于
,则cosA等于
A.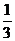 B.
B.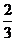 C.
C. D.
D.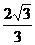
19.如图中的三条抛物线形状相同,关于这三条抛物线叙述错误的是
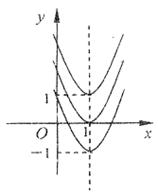
A.三条抛物线的表达式中二次项的系数不一定相同
B.三条抛物线的顶点的横坐标相同
C.当 时,三条抛物线各自的
时,三条抛物线各自的 值都随
值都随 的增大而增大
的增大而增大
D.三条抛物线与直线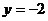 都无交点
都无交点
20.一人乘雪橇沿倾斜角是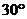 的斜坡滑下,滑下的路程S(米)与时间t(秒)间的关系式为
的斜坡滑下,滑下的路程S(米)与时间t(秒)间的关系式为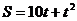 ,若滑到坡底的时间为2秒,则此人下滑的高度为
,若滑到坡底的时间为2秒,则此人下滑的高度为
A.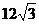 米 D.
米 D.
三、解答题(本大题共6个小题,满分60分,解答时要写出必要的文字说明或演算过程或证明步骤)
21.(满分5分)
在Rt△ABC中,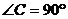 ,
,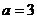 ,
,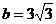 。解这个直角三角形。
。解这个直角三角形。
22.(满分7分)
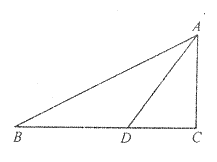
如图,在Rt△ABC中,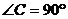 ,
,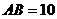 ,
,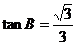 ,试求角平分线AD的长度。
,试求角平分线AD的长度。
23.(满分14分)
抛物线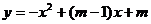 与
与 轴交于(0,3)点。
轴交于(0,3)点。
(1)求出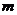 的值并画出这条抛物线;
的值并画出这条抛物线;
(2)求它与 轴的交点和抛物线顶点的坐标;
轴的交点和抛物线顶点的坐标;
(3) 取什么值时,抛物线在
取什么值时,抛物线在 轴上方?
轴上方?
(4) 取什么值时,
取什么值时, 的值随
的值随 值的增大而减少?
值的增大而减少?
24.(满分10分)
如图,山上有一铁塔AB高 ,继续往前走,到F点又刚好能看到塔底B,并测得B的仰角为
,继续往前走,到F点又刚好能看到塔底B,并测得B的仰角为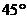 ,已知EF=
,已知EF= )。
)。

25.(满分10分)
随着农业科技的不断发展,农田灌溉也开始采用喷灌的形式(如图甲)。在田间安装一个离开地面一定高度且垂直于地面的喷头,喷头可旋转360。,喷出的水流呈抛物线形状。
如图乙,用OA表示垂直于地面MN的喷头, 米,水流在与OA的距离
米,水流在与OA的距离 )?
)?


26.(满分14分)
如图,在△ABC中, ,
, ,边长为1的正方形的一个顶点D在边AC上,与△ABC另两边分别交于点E、F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设
,边长为1的正方形的一个顶点D在边AC上,与△ABC另两边分别交于点E、F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设 ,正方形与△ABC重叠部分的面积为
,正方形与△ABC重叠部分的面积为 。
。

(1)求 与
与 的函数关系式并写出自变量
的函数关系式并写出自变量 的取值范围;
的取值范围;
(2) 为何值时
为何值时 的值最大?
的值最大?
(3) 在哪个范围取值时
在哪个范围取值时 的值随
的值随 的增大而减小?
的增大而减小?