2008年江苏省启东中学中考模拟考试(六)
数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分
第Ⅰ卷(选择题,共32分)
一、选择题(本题共10小题;第1~8题每小题3分,第9~10题每小题4分,共32分)下列各题都有代号为A、B、C、D的四个结论供选择,其中只有一个结论是正确的.
1.据
A.176×104人次 B.17.6×105人次
C.1.76×106人次 D.0.176×107人次
2.在闭合电路中,电流I,电压U,电阻R之间的关系为: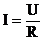 .电压U(V)一定时,电流I(A)关于电阻R(
.电压U(V)一定时,电流I(A)关于电阻R(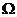 )的函数关系的大致图像是图中的 ( )
)的函数关系的大致图像是图中的 ( )
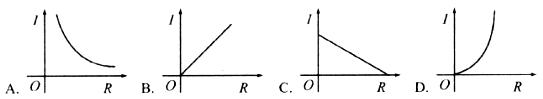
3.一鞋店试销一种新款女鞋,一周内各种型号的鞋卖出的情况如下表所示:
型号
22
22.5
23
23.5
24
24.5
25
数量/双
3
5
10
15
8
4
2
对这个鞋店的经理来说,他最关注的是数据的 ( )
A.平均数 B.众数 C.中位数 D.极差
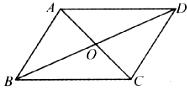
4.如图所示,平行四边形ABCD的周长是48,对角线AC与BD相交于点O,△AOD的周长比△AOB的周长多6,若设AD= ,AB=
,AB= ,则可用列方程组的方法求AD,AB的长,这个方程组可以是 ( )
,则可用列方程组的方法求AD,AB的长,这个方程组可以是 ( )
A.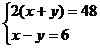 B.
B.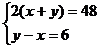
C.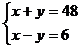 D.
D.
5.李明设计了图中的四种正多边形的瓷砖图案,用同一种瓷砖可以平面密铺的是( )

A.①②④ B.②③④ C.①③④ D.①②③
6.在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有4 个红球且摸到红球的概率为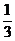 ,那么口袋中球的总数为 ( )
,那么口袋中球的总数为 ( )
A.12个 B.9个 C.6个 D.3个
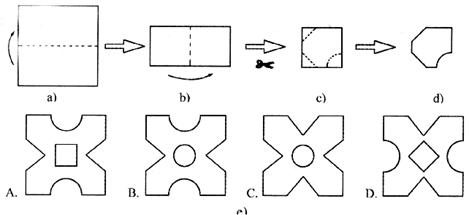
7.将一个正方形纸片依次按图a,图b方式对折,然后沿图c中的虚线裁剪,最后将图d的纸再展开铺平,所看到的图案是图e中的 ( )
8.已知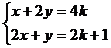 且
且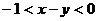 ,则
,则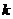 的取值范围为 ( )
的取值范围为 ( )
A.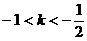 B.
B.
C. D.
D.
9.如图所示,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则APB与CPD的弧长之和为 ( )

A.2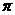 B.
B. C.
C.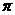 D.
D.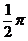
10.如图所示,P是Rt△ABC斜边AB上任意一点(A,B两点除外),过P点作一直线,使截得的三角形与Rt△ABC相似,这样的直线可以作 ( )

A.1条 B.2条 C.3条 D.4条
第Ⅱ卷(共118分)
二、填空题(本题共8小题;每小题3分,共24分)请把最后结果填在题中横线上.
11.( )的相反数是 .
)的相反数是 .
12.函数 中自变量
中自变量 的取值范围是
.
的取值范围是
.
13.如图所示,将长为


14.已知 ,则
,则 的值是
.
的值是
.
15.如图,小亮从A点出发前进

16.如图所示,⊙I是△ABC的内切圆,D,E,F为三个切点,若∠DEF=52°,则∠A的度数为 .

17.如图所示,是用形状、大小完全相同的等腰梯形密铺成的图案,则这个图案中的等腰梯形的底角(指钝角)是 度.

18.如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线 发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为
.
发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为
.

三、解答题(本大题共10小题;共94分)
19.(本题6分)计算: °.
°.
20.(本题满分7分)先化简,再求值: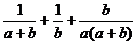 ,其中
,其中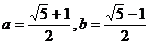 .
.
21.(本题满分6分)用配方法解方程:
22.(本题12分)有两个可以自由转动的均匀转盘A,B都被分成了3等份,并在每一份内均标有数字,如图所示,规则如下:
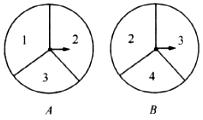
①分别转动转盘A,B;②两个转盘停止后观察两个指针所指份内的数字(若指针停在等份线上,那么重转一次,直到指针指向某一份内为止).
(1)用列表法(或树状图)分别求出“两个指针所指的数字都是方程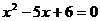 的解”的概率和“两个指针所指的数字都不是方程
的解”的概率和“两个指针所指的数字都不是方程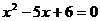 的解”的概率.
的解”的概率.
(2)王磊和张浩想用这两个转盘作游戏,他们规定:若“两个指针所指的数字都是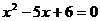 的解”时,王磊得1分;若“两个指针所指的数字都不是
的解”时,王磊得1分;若“两个指针所指的数字都不是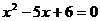 的解”时,张浩得3分,这个游戏公平吗?若认为不公平,请修改得分规定,使游戏对双方公平.
的解”时,张浩得3分,这个游戏公平吗?若认为不公平,请修改得分规定,使游戏对双方公平.
23.(本题满分9分)某网站公布了某城市一项针对2006年第一季度购房消费需求的随机抽样调查结果,图a、图b分别是根据调查结果制作的购房群体可接受价位情况的比例条形统计图和扇形统计图的一部分.
请根据统计图中提供的信息回答下列问题:
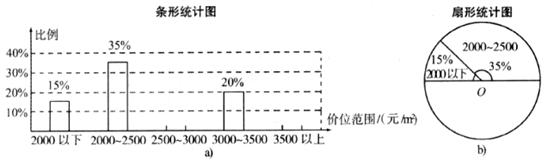
(1)若2500~3000可接受价位所占比例是3500以上可接受价位所占比例的5倍,则这两个可接受价位所占的百分比分别为 .
(2)补全条形统计图和扇形统计图 .
(3)购房群体中所占比例最大的人群可接受的价位是 .
(4)如果2006年第一季度该市所有的有购房需求的人数为50000人,试估计这些有购房需求的人中可接受3500元/m2以上价位的人数是 人.
24.(本题10分)我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称 , 。
(2)如图(1),已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你画出以格点为顶点,OA,OB为勾股边且对角线相等的勾股四边形OAMB.
(3)如图(2),将三角形ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD,DC,∠DCB=30°.求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
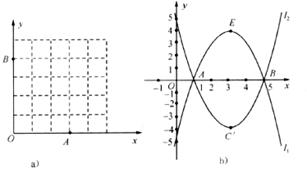
25.(本题满分10分)如图所示,在宽为
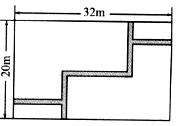
26.(本题满分10分)如图所示,AB是⊙O的直径,AC是弦,OD⊥AB交AC于点D.若
∠A=30°,OD=
27.(本题满分11分)一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.
(1)求出月销售量 (万件)与销售单价
(万件)与销售单价 (元)之间的函数关系式(不必写出
(元)之间的函数关系式(不必写出 的取值范围);
的取值范围);
(2)求出月销售利润 (万元)(利润一售价一成本价)与销售单价
(万元)(利润一售价一成本价)与销售单价 (元)之间的函数关系式(不必写出
(元)之间的函数关系式(不必写出 的取值范围);
的取值范围);
(3)请你通过(2)中的函数关系式及其大致图像帮助公司确定产品的销售单价范围,使月销售利润不低于480万元.
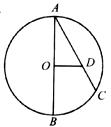
28.(本题13分)
如图所示,已知与 轴交于点A(1,0)和B(5,0o)的抛物线
轴交于点A(1,0)和B(5,0o)的抛物线 的顶点为C(3,4),抛物线
的顶点为C(3,4),抛物线 与
与 关于
关于 轴对称,顶点为C.
轴对称,顶点为C.

(1)求抛物线 的函数关系式;
的函数关系式;
(2)已知原点O,定点D(0,4), 上的点P与
上的点P与 上的点P始终关于
上的点P始终关于 轴对称,则当点P’运动到何处时,以点D,O,P,P’为顶点的四边形是平行四边形?
轴对称,则当点P’运动到何处时,以点D,O,P,P’为顶点的四边形是平行四边形?
(3)在 上是否存在点M,使△ABM是以AB为斜边且一个角为30°的直角三角形?若存,求出点M的坐标;若不存在,说明理由.
上是否存在点M,使△ABM是以AB为斜边且一个角为30°的直角三角形?若存,求出点M的坐标;若不存在,说明理由.
2008年江苏省启东中学中考模拟考试(六)
一、选择题
1.选C; 科学计数法应表示为 的形式,其中1≤
的形式,其中1≤ <10.
<10.
2.选A; 在 中,电压U(V)一定时,电流I(A)关于电阻R(
中,电压U(V)一定时,电流I(A)关于电阻R( )的函数关系为反比例函数,图像为双曲线,但I、R均不能为负.
)的函数关系为反比例函数,图像为双曲线,但I、R均不能为负.
3.选B; 鞋店的经理关注众数,因为众数影响他的进货决定.
4.选A; 平行四边形的对边相等,所以周长等于邻边之和的2倍;因为BO=DO,所以△AOD的周长与△AOB的周长之差就是AD与AB的差.
5.选A; 用同一种图形可以平面镶嵌的是正三、四、六边形.
6.选A; 口袋中球的总数为4÷ 12.
12.
7.选D; 利用轴对称思想进行图形还原即可.
8.选D; 两条等式相减就得到 的不等式.
的不等式.
二、填空题
9. 10.
10. 11.
11.
16.3≤b≤6
三、解答题
19.解:原式=1+3-2× =4-1=3.
=4-1=3.
20.解:原式=
∵ ,
, ∴原式=
∴原式=
21.解:两边都除以2,得 . 移项得
. 移项得 .
.
配方得 ,
, .∴
.∴ 或
或 .
.
∴ .
.
22.解:(1)解方程 得
得 列表:
列表:
2
3
4
1
1,2
1,3
1,4
2
2,2
2,3
2,4
3
3,2
3,3
3,4
(或用树状图)
由表知:指针所指两数都是该方程解的概率是: ;指针所指两数都不是该方程解的概率是:
;指针所指两数都不是该方程解的概率是:
(2)不公平!∵1× ≠3×
≠3×
修改得分规则为:指针所指两个数字都是该方程解时,王磊得1分;指针所指两个数字都不是该方程解时,张浩得4分.此时1× =4×
=4×
23.(1)25% 5% (2)见图(补全每个图给2分)

(3)2000~2500(元/m2) (4)2500
24.(1)正方形、长方形、直角梯形.(任选两个均可)(填正确一个得1分)
(2)答案如图所示.M(3,4)或M(4,3).(没有写出不扣分)(根据图形给分,一个图形正确得l分)

(3)证明:连接EC,∵△ABC≌△DBE,∴.AC=DE,BC=BE.∵∠CBE=60°
∴EC=BC.∠BCE=60° ∵∠DCB=30° ∴∠DCE=90° ∴DC2+EC2=DE2
∴DC2+BC2=AC2.即四边形ABCD
25.解法(1):由题意转化为图a,设道路宽为 m(没画出图形不扣分)
m(没画出图形不扣分)

根据题意,可列出方程为
整理得
解得 50(舍去),
50(舍去), 2
2
答:道路宽为
解法(2):由题意转化为图b,设道路宽为 m,根据题意列方程得:
m,根据题意列方程得:


整理得:
解得: (舍去)
(舍去)
答:道路宽为
26.解法(1):∵OD⊥AB,∠A=30°
∴OA=OD÷tan30°=20 ,AD=2OD=40.
,AD=2OD=40.
∵AB是⊙O的直径,∴AB=40 ,且∠ACB=90°
,且∠ACB=90°
∴AC=AB?cos30°-40 ×
× 60
60
∴DC=AC-AD=60-40=20(cm)
解法(2):过点O作OE⊥AC于点E,如图
∵OD⊥AB于点O,∠A=30°,
∴AD=2OD=40,AO=OD÷tan30°=20
∴AE=AO?cos30°-20 ×
× 30
30
∵OE⊥AC于点E ∴AC=2AE=60.∴DC=AC-AD=60-40=20(cm)
解法(3):∵OD⊥AB于点O,AO=BO,∴AD=BD.∴∠1=∠A=30°
又∵AB为⊙O直径,∴∠ABC=60°.∴∠2=60°-30°=30°=∠A
又∵∠AOD=∠C=90°.∴△AOD≌△BCD ∴DC=OD=20(cm)

27.解:(1) .
.
∴ 与
与 的函数关系式为
的函数关系式为 .
.
(2) .
.
∴ 与
与 的函数关系式为
的函数关系式为 .
.
(3)令 480,得
480,得 ,
,
整理得 ,解得
,解得 .
.
将二次函数解析式变形为 画出大致图像如图.
画出大致图像如图.
由图像可知,要使月销售利润不低于480万元,产品的销售单价应在30元到38元之间(即30≤ ≤38).
≤38).

说明:解答题各小题只给了一种解答及评分说明,其他解法只要步骤合理、解答正确,均应给出相应分数.
28.解:(1)由题意知点C’的坐标为(3,-4).
设 的函数关系式为
的函数关系式为 .
.
又∵点A(1,0)在抛物线 上,∴
上,∴ ,解得
,解得 1.
1.
∴抛物线 的函数关系式为
的函数关系式为 (或
(或 ).
).
(2)∵P与P’始终关于 轴对称,∴PP’与
轴对称,∴PP’与 轴平行.
轴平行.
设点P的横坐标为m,则其纵坐标为 ,∵OD=4,
,∵OD=4,
∴ ,即
,即 .
.
当 时,解得
时,解得 .
.
当 时,解得
时,解得 .
.
∴当点P运动到( ,2)或(
,2)或( ,2)或(
,2)或( ,-2)或(
,-2)或( ,-2)时,
,-2)时,
P’P OD,以点D,O,P,P’为顶点的四边形是平行四边形.
OD,以点D,O,P,P’为顶点的四边形是平行四边形.
(3)满足条件的点M不存在.理由如下:若存在满足条件的点M在 上,
上,
则∠AMB=90°,∵∠RAM=30°(或∠ABM=30°),∴BM= AB=
AB= ×4=2.
×4=2.
过点M作MF⊥AB于点F,可得∠BMF=∠BAM=30°.
∴FB= BM=
BM= ×2=1,FM=
×2=1,FM= ,OF=4.
,OF=4.
∴点M的坐标为(4, ).
).
但是,当 4时,
4时, .
.
∴不存在这样的点M构成满足条件的直角三角形。