1．下列各数中，最小的数是   （　　）

　　A．－1                    　B．0                     　　C．1                 　　　D． 

2．方程4x－1＝3的解是    （　　）

　A．x＝－1               　B．x＝1                　　C．x＝－2         　　　D．x＝2

3．由4个相同的小立方块搭成的几何体如图所示，它的左视图是 （　　） 

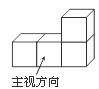
A．　　　　　     B．　　　　C．　　　      D．　

4．若分式的值为零，则x的值是　　（　　）

　　A．0                    　　B．1                     　　C．－1              　　　D．－2

5．抛物线y＝(x－1)²＋3的对称轴是　　（　　）

　A．直线x＝1           　B．直线x＝3        　　C．直线x＝－1 　　　D．直线x＝－3

6．已知反比例函数y＝的图象经过点（3，－2），则k的值是（　　）

　A．－6          　　　　B．6 　　　　　　　  C．     　　　　　　D．－

7．如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD＝2，AC＝3，则sinB的值是（　　）

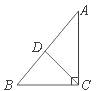
A．　　　　　　          B．　　　　　　　C．　　                 D．

8．已知⊙O₁和⊙O₂外切，它们的半径分别为2cm和5cm，则O₁O₂的长是（　　）

　　A．2cm                    　B．3cm                　　C．5cm             　　　D．7cm

9．体育老师对九年级（1）班学生“你最喜欢的体育项目是什么？（只写一项）”的问题进行了调查，把所得数据绘制成频数分布直方图（如图）．由图可知，最喜欢篮球的频率是                                        （　　）

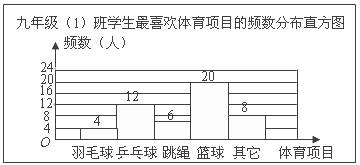
　A．0.16                   　B．0.24                　　C．0.3              　　　D．0.4

10．以OA为斜边作等腰直角三角形OAB，再以OB为斜边在△OAB外侧作等腰直角三角形OBC，如此继续，得到8个等腰直角三角形（如图），则图中△OAB与△OHJ的面积比值是                                （　　）

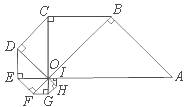
A．32                        　B．64                   　　C．128              　　　D．256

11．分解因式：x²－9＝___________．

12．布袋中装有2个红球，3个白球，5个黑球，它们除颜色外均相同，则从袋中任意摸出一个球是白球的概率是__________．

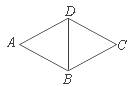
13．如图，菱形ABCD中，∠A＝60º，对角线BD＝8，则菱形ABCD的周长等于______．

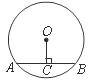
14．如图，⊙O的半径为5，弦AB＝8，OC⊥AB于C，则OC的长等于__________．

15．为了奖励兴趣小组的同学，张老师花92元钱购买了《智力大挑战》和《数学趣题》两种书．已知《智力大挑战》每本18元．《数学趣题》每本8元，则《数学趣题》买了______本．

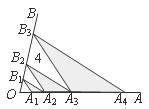
16．如图，点A₁，A₂，A₃，A₄在射线OA上，点B₁，B₂，B₃在射线OB上，且A₁B₁∥A₂B₂∥A₃B₃，A₂B₁∥A₃B₂∥A₄B₃．若△A₂B₁B₂，△A₃B₂B₃的面积分别为1，4，则图中三个阴影三角形面积之和为____________．

17．（本题10分）

（1）计算：－(－1)⁰＋｜－1｜．

（2）我们已经学习了一元二次方程的四种解法：因式分解法，开平方法，配方法和公式法．请从以下一元二次方程中任选一个，并选择你认为适当的方法解这个方程．

①x²－3x＋1＝0；②(x－1)²＝3；③x²－3x＝0；④x²－2x＝4．

18．（本题8分）如图，在直角坐标系中，Rt△AOB的两条直角边OA，OB分别在x轴的负半轴，y轴的负半轴上，且OA＝2，OB＝1．将Rt△AOB绕点O按顺时针方向旋转90º，再把所得的像沿x轴正方向平移1个单位，得△CDO．

（1）写出点A，C的坐标；

（2）求点A和点C之间的距离．

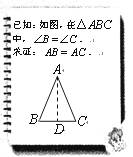
19．（本题9分）文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时，画出图形，写出“已知”，“求证”（如图），她们对各自所作的辅助线描述如下：

文文：“过点A作BC的中垂线AD，垂足为D”；

彬彬：“作△ABC的角平分线AD”．

数学老师看了两位同学的辅助线作法后，说：“彬彬的作法是正确的，而文文的作法需要订正．”

（1）请你简要说明文文的辅助线作法错在哪里．

（2）根据彬彬的辅助线作法，完成证明过程．

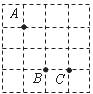
20．（本题9分）如图，方格纸中有三个点A，B，C，要求作一个四边形使这三个点在这个四边形的边（包括顶点）上，且四边形的顶点在方格的顶点上．

（1）在图甲中作出的四边形是中心对称图形但不是轴对称图形；

（2）在图乙中作出的四边形是轴对称图形但不是中心对称图形；

（3）在图丙中作出的四边形既是轴对称图形又是中心对称图形．

图甲         图乙         图丙

21．（本题10分）一次奥运知识竞赛中，一共有25道题，答对一题得10分，答错（或不答）一题扣5分．设小明同学在这次竞赛中答对x道题．

（1）根据所给条件，完成下表：

答题情况

答对

答错或不答

题数

_x

每题分值

₁₀

_－5

得分

_10x

（2）若小明同学的竞赛成绩超过100分，则他至少答对几道题？

22．（本题10分）一次函数y＝x－3的图象与x轴，y轴分别交于点A，B．一个二次函数y＝x²＋bx＋c的图象经过点A，B．

（1）求点A，B的坐标，并画出一次函数y＝x－3的图象；

（2）求二次函数的解析式及它的最小值．

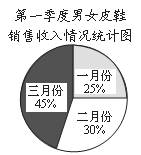
23．（本题10分）温州皮鞋畅销世界，享誉全球．某皮鞋专卖店老板对第一季度男女皮　　　鞋的销售收入进行统计，并绘制了扇形统计图（如图）．由于三月份开展促销活动，男、女皮鞋的销售收入分别比二月份增长了40%，60%．已知第一季度男女皮鞋的销售总收入为200万元．

（1）一月份销售收入______________万元，二月份销售收入_____________万元，三月份销售收入__________万元；

（2）二月份男、女皮鞋的销售收入各是多少万元？

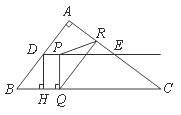
24．（本题14分）如图，在Rt△ABC中，∠A＝90º，AB＝6，AC＝8，D，E分别是边AB，AC的中点，点P从点D出发沿DE方向运动，过点P作PQ⊥BC于Q，过点Q作QR∥BA交AC于R，当点Q与点C重合时，点P停止运动．设BQ＝x，QR＝y．

（1）求点D到BC的距离DH的长；

（2）求y关于x的函数关系式（不要求写出自变量的取值范围）；

（3）是否存在点P，使△PQR为等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由．