2008年河北省初中毕业生学业考试模拟试卷(一)
数学
本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.
本试卷满分为120分,考试时间为120分钟.
卷Ⅰ(选择题,共20分)
注意事项:1.答卷I前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上,考试结束,监考人员将试卷和答题卡一并收回.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效.
一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.绝对值为4的实数是
A.±4 B.
2.下图是由一些相同的小正方体构成的几何体的三视图.

这些相同的小正方体的个数是
A.4个 B.5个 C.6个 D.7个
3.把不等式组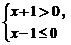 的解集表示在数轴上,正确的是
的解集表示在数轴上,正确的是
 A B
C
D
A B
C
D
4.化简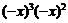 ,结果正确的是
,结果正确的是
A. B.
B. C.
C. D.
D.
5.小明设计了一个关于实数运算的程序:输出的数比该数的平方小1,小刚按此程序输入 后,输出的结果应为
后,输出的结果应为
A.10
B.
6.如图1,把一个正方形纸片三次对折后沿虚线剪下,打开铺平后,得到的图形是

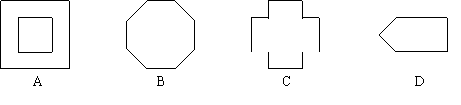
7.甲( ),乙(●),丙(■)表示的是三种不同的物体,现用天平称了两次,如图2所示,那么这三种物体按质量从大到小的顺序应是
),乙(●),丙(■)表示的是三种不同的物体,现用天平称了两次,如图2所示,那么这三种物体按质量从大到小的顺序应是

A. 甲 乙 丙 B.乙 甲 丙
C. 甲 丙 乙 D.丙 乙 甲
8.图3所示的两个圆盘中,指针落在每一个数字所在的扇形区域上的机会是相等的,那么两个指针同时落在偶数所在的扇形区域上的概率是

A. B.
B. C.
C. D.
D.
9.⊙O1与⊙O2的半径分别为2和5,当O1O2=3.5时,两圆的位置关系是
A. 外切 B .相交 C . 内切 D. 内含
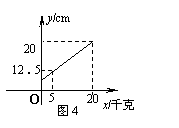
10.若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数,图象如图4所示,由图可知,不挂重物时,弹簧的长度是
A.
卷II(非选择题,共100分)
二、填空题(本大题共5个小题;每小题3分,共15分.把答案写在题中横线上)
11.分解因式 =
.
=
.
12.函数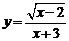 的自变量x的取值范围是 .
的自变量x的取值范围是 .
13.如图5是用4个全等的等腰梯形镶嵌成的图形,则这个图形中等腰梯形上下两底边的比是 .


14.用换元法解分式方程 时,若设
时,若设 ,则由原方程化成的关于y的整式方程为
.
,则由原方程化成的关于y的整式方程为
.
15.如图6,一牧童在A处牧马,牧童家在B处,A,B处距河岸的距离AC,BD分别为
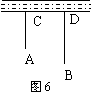

三、解答题(本大题共10个小题;共85分)
16.(本小题满分7分)
已知:a=2,求(1+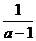 )?(a2-1)值.
)?(a2-1)值.
17.(本小题满分7分)
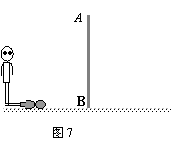
如图7,小丽在观察某建筑物 .
.
(1)请你根据小亮在阳光下的投影,画出建筑物 在阳光下的投影.
在阳光下的投影.
(2)已知小丽的身高为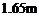 ,在同一时刻测得小丽和建筑物
,在同一时刻测得小丽和建筑物 的投影长分别为
的投影长分别为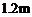 和
和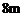 ,求建筑物
,求建筑物 的高.
的高.

18.(本小题满分7分)
观察右表中数字的排列规律,回答下面的问题
1
3
5
7
…
2
6
10
14
…
4
12
20
28
…
8
24
40
56
…
…
…
…
…
…
①表中第1行第5列的数字是 ;
②表中第5行第4列的数字是 ;
③请用关于n的代数式表示表中第3列第n行的数为 ;
④数字2006的位置是第 行,第 列.
19.(本小题满分8分)
甲、乙两个商场在同一周内经营同一种商品,每天的获利情况如下表:
日 期
星期一
星期二
星期三
星期四
星期五
星期六
星期日
甲商场获利/万元
2.5
2.4
2.8
3
3.2
3.5
3.6
乙商场获利/万元
1.9
2.3
2.7
2.6
3
4
4.5
(1)请你计算出这两个商场在这周内每天获利的平均数,并说明这两个商场本周内总的获利情况;
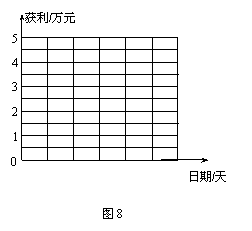
(2)在图8所示的网格图内画出两个商场每天获利的折线图;(甲商场用虚线,乙商场用实线)
(3)根据折线图请你预测下周一哪个商场的获利会多一些?并简单说出你的理由.








20.(本小题满分8分)
某少儿活动中心在“六?一”活动中,举行了一次转盘摇奖活动.如图9是一个可以自由转动的转盘,当转动停止时,指针落在哪一个区域就可以获得相应的奖品(落在分界线上时重新摇奖).下表是活动进行中统计的有关数据.


(1)计算并完成表格:
转动转盘的次数n
100
150
200
500
800
1000
落在“铅笔”区域中的次数m
68
111
136
352
556
701
落在“铅笔”区域中的频率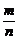
(2)当转动转盘的次数n很大时,概率将会接近多少?
21.(本小题满分8分)
某市自来水公司为鼓励居民节约用水,采取每月用水量分段收费的办法,每户居民应交水费y(元)与用水量x(吨)之间的函数关系如图10所示.
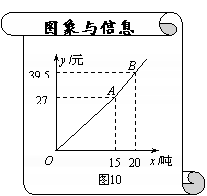

(1)分别求出当0≤x≤15和x≥15时,y与x的函数关系式;
(2)若一用户在某月的用水量为21吨,则应交水费多少元?
22.(本小题满分8分)
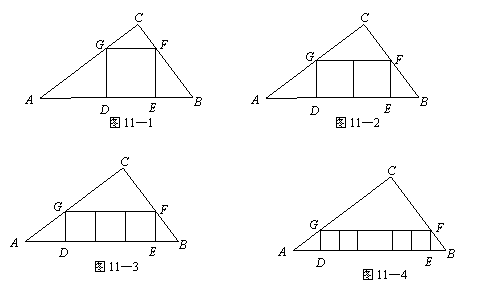

如图11―1,在△ABC中,∠C=90°,AC=4,BC=3,四边形DEFG为△ABC的内接正方形,若设正方形的边长为x,容易算出x的长为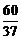 .
.
探究与计算:
(1)如图11―2,若三角形内有并排的两个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为 ;
(2)如图11―3,若三角形内有并排的三个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为 .
猜想与证明:
如图11―4,若三角形内有并排的n个全等的正方形,它们组成的矩形内接于△ABC,请你猜想正方形的边长是多少?并对你的猜想进行证明.


解决问题:
(1)设图12―2中的矩形ACBD和矩形AEFB的面积分别为S1和S2,则S1 S2(填“>”,“=”或“< ;
;
(2)如图12―3中的△ABC是锐角三角形,且三边满足BC>AC>AB,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出 个,并在图12―3中把符合要求的矩形画出来.


猜想证明:
(1)在图12―3中所画出的矩形中,它们的面积之间具有怎样的关系?并说明你的理由;
(2)猜想图12―3中所画的矩形的周长之间的大小关系.
24.(本小题满分12分)
某商店经营一批进价为2元的小商品,在市场营销的过程中发现:如果该商品按最低价3元销售,日销售量为18件,如果单价每提高1元,日销售量就减少2件.设销售单价为x(元),日销售量为y(件).
(1)写出日销售量y(件)与销售单价x(元)之间的函数关系式;
(2)设日销售的毛利润(毛利润=销售总额-总进价)为P(元),写出毛利润P(元)与销售单价x(元)之间的函数关系式;
(3)在图13所示的坐标系中画出P关于x的函数图象的草图,并标出顶点的坐标;


(4)观察图象,说出当销售单价为多少时,日销售的毛利润最高?是多少?
25.(本小题满分12分)
有一根直尺的短边长
(1)当x=0时,S=_____________;当x = 10时,S =______________;
(2)当0<x≤4时,如图14―2,求S与x的函数关系式;
(3)当6<x<10时,求S与x的函数关系式;
(4)请你作出推测:当x为何值时,阴影部分的面积最大?并写出最大值.
(说明:问题(4)是额外加分题,加分幅度为1~4分)







