2008年河北省初中毕业生升学模拟考试(二)
数 学 试 卷
本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.
本试卷满分为120分,考试时间为120分钟.
卷Ⅰ(选择题,共20分)
得 分
评卷人
一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.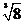 的相反数是………………………………………………………………【 】
的相反数是………………………………………………………………【 】
A.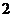 B.
B.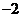 C.
C.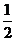 D.
D.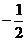
2.
 A
A 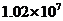 B
B 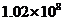 C
C 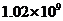 D
D 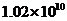
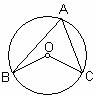
3. 如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是…【 】
A.50° B.100° C.130° D.200°
4. 下面四个几何体中,主视图、左视图、俯视图是全等图形的几何图形是【 】
A.圆柱 B.正方体 C.三棱柱 D.圆锥
5.“义乌中国小商品城指数” 简称“义乌指数”.下图是
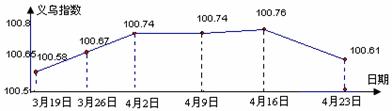
A.
6.某校九年级(1)班50名学生中有20名团员,他们都积极报名参加某市“文明劝导活动”.根据要求,该班从团员中随机抽取1名参加,则该班团员京京被抽到的概率是………………………………………………………………………………………【 】
 A.
A.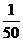 B.
B.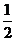 C.
C.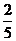 D.
D.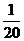
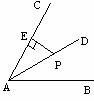
7. 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.
已知PE=3,则点P到AB的距离是………………………【 】
A.3 B.
8. 如图,花园内有一块边长为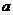 的正方形土地,园艺师设计了四种不同图案,其中的阴影部分用于种植花草,种植花草面积最大的是【
】
的正方形土地,园艺师设计了四种不同图案,其中的阴影部分用于种植花草,种植花草面积最大的是【
】
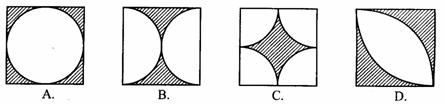
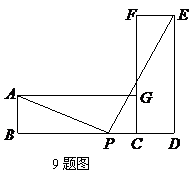 9. 如图,矩形
9. 如图,矩形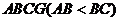 与矩形
与矩形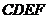 全等,点
全等,点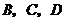 在同一条直线上,
在同一条直线上,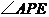 的顶点
的顶点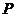 在线段
在线段 上移动,使
上移动,使 为直角的点
为直角的点 的个数是……………【
】A.0 B.
的个数是……………【
】A.0 B.
10.某商场在促销期间规定:商场内所有商品按标价的80%出售,同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券.(奖券购物不再享受优惠)
消费金额x的范围(元)
200≤x<400
400≤x<500
500≤x<700
…
获得奖券的金额(元)
30
60
100
…
根据上述促销方法,顾客在该商场购物可获得双重优惠,如果胡老师在该商场购标价450元的商品,他获得的优惠额为_……………【 】
A.100元 B.110元 C.120元 D.140元
总 分
核分人
2008年河北省初中毕业生升学模拟考试
数 学 试 卷
卷II(非选择题,共100分)
得 分
评卷人
二、填空题(本大题共8个小题;每小题3分,共24分.把答案
 写在题中横线上)
写在题中横线上)
11.当x=2时,代数式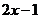 的值为_______.
的值为_______.
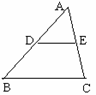
12.如图,在△ABC中,点D、E分别是边AB、AC的中点,
已知DE=6cm,则BC=______cm.
13.已知反比例函数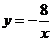 的图象经过点P(a+1,4),则a=______.
的图象经过点P(a+1,4),则a=______.
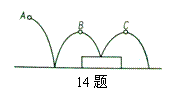 14. 一个有弹性的球从A点下落到地面,弹起到B点后又落 下到高20厘米的平台上,再弹起到C点,最后落到地面(如图),已知每次弹起的高度都是落下高度的80%,A点离地面比C点离地面高出68厘米的高度,则C点离地面的高度是 .
14. 一个有弹性的球从A点下落到地面,弹起到B点后又落 下到高20厘米的平台上,再弹起到C点,最后落到地面(如图),已知每次弹起的高度都是落下高度的80%,A点离地面比C点离地面高出68厘米的高度,则C点离地面的高度是 .
15.袋中装有3个红球,1个白球它们除了颜色相同以外都相同,随机从中摸出一球,记下颜色后放回袋中,充分摇匀后再随机摸出一球,两次都摸到红球的概率是______.
16.如图,⊙M与x轴相切于原点,平行于y轴的直线PQ交⊙M 于P、Q两点,P点在Q点的下方. 若点P的坐标是(2,1),则圆心M的坐标是____________.
17.如图是由两个具有公共顶点A的正方形组成的图形,且其中一个正方形的顶点D在另一个正方形的边BC上(点D不与点B、C重合).则∠DCE= .
18.如图,点E(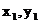 )、F(
)、F(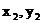 )在抛物线
)在抛物线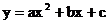 的对称轴的同侧 (点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积,则S与y1、y2的数量关系式为:
的对称轴的同侧 (点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积,则S与y1、y2的数量关系式为:
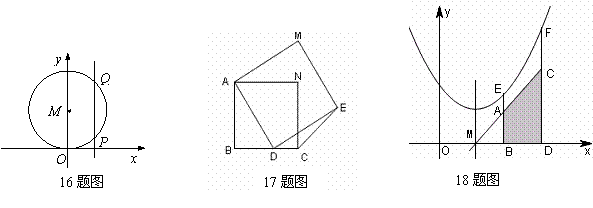 S=
S=
得 分
评卷人
三、解答题(本大题共8个小题;共76分.解答应写出文字说明、证明过程或演算步骤)
19.(本小题满分7分)
解方程: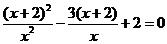 .
.
得 分
评卷人
20.(本小题满分7分)
不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为.
(1)试求袋中蓝球的个数.
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用树状图或列表法,求两次摸到都是白球的概率.
得 分
评卷人
21.(本小题满分10分)
已知: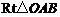 在直角坐标系中的位置如图所示,
在直角坐标系中的位置如图所示,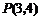 为
为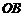 的中点,点
的中点,点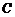 为折线
为折线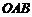 上的动点,线段
上的动点,线段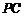 把
把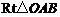 分割成两部分.
分割成两部分.
问:点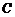 在什么位置时,分割得到的三角形与
在什么位置时,分割得到的三角形与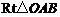 相似?
相似?
 (注:在图上画出所有符合要求的线段
(注:在图上画出所有符合要求的线段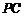 ,并求出相应的点
,并求出相应的点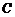 的坐标).
的坐标).
得 分
评卷人
22.(本小题满分8分)
 已知:如图,在
已知:如图,在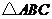 中,
中,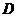 为
为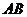 边上一点,
边上一点,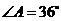 ,
,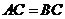 ,
,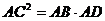 .
.
(1)试说明: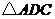 和
和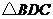 都是等腰三角形;
都是等腰三角形;
(2)若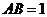 ,求
,求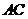 的值;
的值;
(3)请你构造一个等腰梯形,使得该梯形连同它的两条对角线得到8个等腰三角形.(标明各角的度数)
得 分
评卷人
23.(本小题满分10分)
某公司年初推出一种高新技术产品,该产品销售的累积利润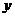 (万元)与销售时间
(万元)与销售时间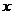 (月)之间的关系(即前
(月)之间的关系(即前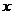 个月的利润总和
个月的利润总和 与
与 之间的关系)为
之间的关系)为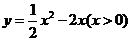 .
.
(1)求出这个函数图象的顶点坐标和对称轴;
(2)请在所给坐标系中,画出这个函数图象的简图;
(3)根据函数图象,你能否判断出公司的这种新产品销售累积利润是从什么时间开始盈利的?
(4)这个公司第6个月所获的利润是多少?
 |
得 分
评卷人
24.(本小题满分10分)
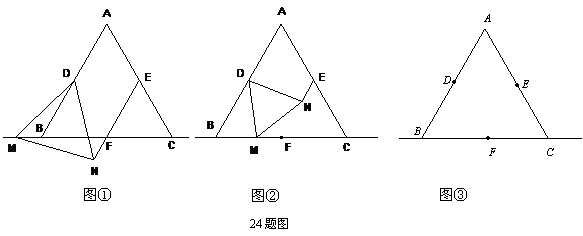
如图, 已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时, △DMN也随之整体移动) .
(1)如图①,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必证明或说明理由;
(2)如图②,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图②证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN与MF的数量关系是否仍然成立?若成立?请直接写出结论,不必证明或说明理由.

得 分
评卷人
25.(本小题满分12分)
某公司专销产品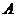 ,第一批产品
,第一批产品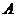 上市40天内全部售完.该公司对第一批产品
上市40天内全部售完.该公司对第一批产品 上市后的市场销售情况进行了跟踪调查,调查结果如图所示,其中图1中的折线表示的是市场日销售量与上市时间的关系;图2中的折线表示的是每件产品
上市后的市场销售情况进行了跟踪调查,调查结果如图所示,其中图1中的折线表示的是市场日销售量与上市时间的关系;图2中的折线表示的是每件产品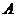 的销售利润与上市时间的关系.
的销售利润与上市时间的关系.
(1)试写出第一批产品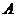 的市场日销售量
的市场日销售量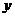 与上市时间
与上市时间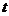 的关系式;
的关系式;
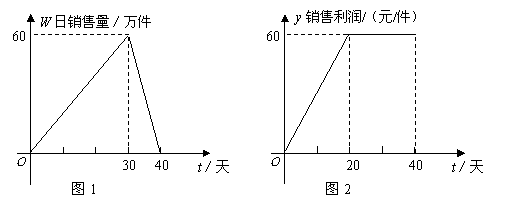 (2)第一批产品
(2)第一批产品 上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?(说明理由)
上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?(说明理由)
得 分
评卷人
26.(本小题满分12分)
如图,在平面直角坐标系中,直角梯形 的边
的边 落在
落在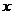 轴的正半轴上,且
轴的正半轴上,且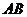 ∥
∥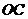 ,
,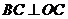 ,
,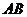 =4,
=4,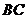 =6,
=6,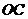 =8.正方形
=8.正方形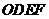 的两边分别落在坐标轴上,且它的面积等于直角梯形
的两边分别落在坐标轴上,且它的面积等于直角梯形 面积.将正方形
面积.将正方形 沿
沿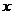 轴的正半轴平行移动,设它与直角梯形
轴的正半轴平行移动,设它与直角梯形 的重叠部分面积为
的重叠部分面积为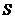 .
.
(1)求正方形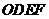 的边长;
的边长;
(2)①正方形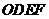 平行移动过程中,通过操作、观察,试判断
平行移动过程中,通过操作、观察,试判断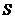 (
(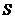 >0)的变化情况是 ;
>0)的变化情况是 ;
A.逐渐增大 B.逐渐减少 C.先增大后减少 D.先减少后增大
②当正方形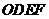 顶点
顶点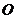 移动到点
移动到点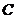 时,求
时,求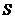 的值;
的值;
(3) 设正方形
设正方形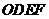 的顶点
的顶点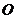 向右移动的距离为
向右移动的距离为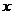 ,求重叠部分面积
,求重叠部分面积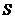 与
与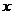 的函数关系式.
的函数关系式.
|

 ;
16.(0,2.5) 17.135° 18.
;
16.(0,2.5) 17.135° 18. 
 ,……………………(4分)
,……………………(4分) x=2………………………………………(5分)
x=2………………………………………(5分) 个
-------1分
个
-------1分 -------2分
-------2分
 答:蓝球有1个
--------3分
答:蓝球有1个
--------3分 =
= ----------7分
----------7分 作
作 ,垂足是
,垂足是 ,
, .
. .???????????????????????????????????????????????? 2分
.???????????????????????????????????????????????? 2分 过
过 ,垂足是
,垂足是 ,
, .
. .??????????????????????????????????????????????? 4分
.??????????????????????????????????????????????? 4分 ,垂足是
,垂足是 ,
, .????????????????????? 6分
.????????????????????? 6分 ,
, ,
, .???????????????????????????? 8分
.???????????????????????????? 8分 点
点 坐标是
坐标是 .??????????????????????????????????????????????????????????????????????????????????????????????????? 9分
.??????????????????????????????????????????????????????????????????????????????????????????????????? 9分 有三个,其连线段分别是
有三个,其连线段分别是 (如图).????????????????????????????? 10分
(如图).????????????????????????????? 10分 中,
中, ,
, .????????????????????????????????????????????????????????????????????? 1分
.????????????????????????????????????????????????????????????????????? 1分 中,
中, ;
;
 .
. ?????????????????????????????????????????????????????????????????????????????????????????????? 2分
?????????????????????????????????????????????????????????????????????????????????????????????? 2分 .
. 和
和 都是等腰三角形.4分
都是等腰三角形.4分 ,则
,则 ,即
,即 .??????????????????????????????????????? 4分
.??????????????????????????????????????? 4分 (负根舍去).?????????????????????????????????????????????????????? 6分
(负根舍去).?????????????????????????????????????????????????????? 6分 (3)
(3) .???????????????????????????????????????????????????????? 2分
.???????????????????????????????????????????????????????? 2分 函数图象的顶点坐标为
函数图象的顶点坐标为 ,对称轴为直线
,对称轴为直线 .?????????????????????????????????????? 4分
.?????????????????????????????????????? 4分 (4)
(4) 时,
时, ,
, 时,
时, ,
,
 万元.
10分
万元.
10分 ∴MF=NE.
?????????????????????????? 9分
∴MF=NE.
?????????????????????????? 9分
 时,设市场的日销售量
时,设市场的日销售量 .
. 点
点 在图象上,
在图象上, .
. .即
.即 .??????????????????????????????????????????????????????????????????????????????????????????? 2分
.??????????????????????????????????????????????????????????????????????????????????????????? 2分 时,设市场的日销售量
时,设市场的日销售量 .
. 在图象上,
在图象上,
 .
. .????????????????????????????????????????????????????????????????????????????????????????????????? 4分
.????????????????????????????????????????????????????????????????????????????????????????????????? 4分 .???????????????????????????????????????????? 6分
.???????????????????????????????????????????? 6分 (天)时,市场的日销售量达到最大60万件;又由图2知,当
(天)时,市场的日销售量达到最大60万件;又由图2知,当 时,每件产品的日销售利润为
时,每件产品的日销售利润为 ;
; 时,每件产品的日销售利润为
时,每件产品的日销售利润为 .
. ;
; 时,产品的日销售利润
时,产品的日销售利润 最大等于2400万元.
最大等于2400万元. 时,产品的日销售利润
时,产品的日销售利润 .
. 万元;
万元; ;
;
 ∴
∴ ,
, (舍去).………2分
(舍去).………2分 .………………………………………………4分
.………………………………………………4分 .…………………6分
.…………………6分 ∽△
∽△ ,
, ∴
∴ ,
,
 .
. .……………………8分
.……………………8分 
 . ………9分
. ………9分 ,
, .
.
 .…………………………10分
.…………………………10分 ④当8≤
④当8≤
 .…………………………11分
.…………………………11分
 .……………12分
.……………12分