2008年宁津县九年级第一次模拟考试
数学试题
(满分120分,考试时间120分钟) 2008.4
第 I 卷 (选择题 共24分)
一、选择题(本大题共8小题,在每小题给出的四个选项中,只有一项是正确的,请将正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个均记为零分)
1.下列运算正确的是( )
A.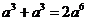 B.
B.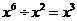 C.
C. 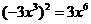 D.
D. 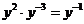
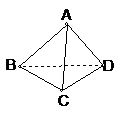
2.大家都知道青蛙“坐井观天”的故事,它只看见井口大的一片天,实际上这与它的视角有关.如图所示,有一只青蛙在一口直径AB为
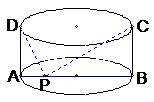
A.45° B.90° C.135° D.无法确定
3.如图,菱形ABCD一内角为60°,边长为2,将它绕对角线的交点O顺时针旋转90°后到A′B′C′D′的位置,则旋转前后两菱形重叠部分多边形的周长为( )
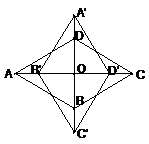
A.
8
B. 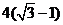 C.
C.  D.
D. 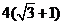 .
.
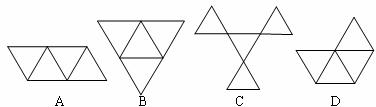
4.如图所示是一个正四面体,它的四个面都是正三角形.现沿它的三条棱AC、BC、CD剪开展成平面图形,则所得展开图是( )
5.如图所示,准备了三张大小相同的纸片,其中两张纸上各画了一个半径相等的半圆,另一张纸上画了一个正方形,两个半圆可以拼成一个圆形,一个半圆和一个正方形可以拼成一个蘑菇形,现将三张纸片放在一个盒子里摇匀,随机地抽取两张,则拼成蘑菇形的概率为( )

A.  B.
B. 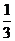 C.
C. 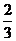 D.
D. 
6.下列四个点中,有三个点在同一直线上,不在同一直线上的点是( )
A.(-3,-1) B.(1,1) C.(3,2) D.(4,3)
7.如图,以两条直线L1、L2的交点坐标为解的方程组是( )
A. B.
B. C.
C. D.
D.

8.如图,正方形OABC、正方形ADEF的顶点A、D、C在坐标轴上,点F在AB上,点B、E在函数  的图象上,则点E的坐标是 ( )
的图象上,则点E的坐标是 ( )

A.  B.
B.
C.  D.
D.
第II卷(非选择题 共96分)
二.填空题(本题共8小题,每小题3分,本题满分24分)
9.已知  ,且 ab>0,则 a+b的值为_______________.
,且 ab>0,则 a+b的值为_______________.
10.计算  _____________.
_____________.
11.如图,△ABC的顶点坐标分别是A(3,6)、B(1,3)、C(4,2),如果将△ABC绕C点按顺时针方向旋转90°,得到△A′B′C′,那么点A的对应点A′的坐标是_____
________.

12.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则BC=___________.

13.已知m、n 是关于x
的方程  的两个实数根,且满足
的两个实数根,且满足
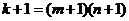 ,则实数k 的值是______________.
,则实数k 的值是______________.
14.数据 6,8,8,x 的众数有两个,这组数据的中位数是_____________.
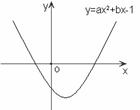
15.已知二次函数 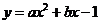 的图象如图所示,则点 (a, b)关于原点的对称点在第_______象限.
的图象如图所示,则点 (a, b)关于原点的对称点在第_______象限.
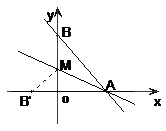
16.直线 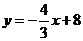 与x 轴、y 轴分别交于点A和点B,M是OB上的一点,若将
与x 轴、y 轴分别交于点A和点B,M是OB上的一点,若将
△ABM沿AM折叠,点B恰好落在 x 轴上的B′处,则直线AM的解析式为__________
__________.
三. 解答题(本大题共8小题,解答过程要写出必要的文字说明、证明过程或演算步骤)
17.(本题满分7分)
先化简,再求值.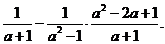 其中
其中 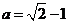
18.(本题满分7分)
解不等式组 把解集表示在数轴上,并写出整数解.
把解集表示在数轴上,并写出整数解.
19.(本题满分8分)
用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为X.
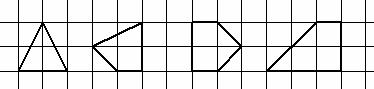
① ② ③ ④
(1)如上图所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和对应关系如下表:
多边形序号
①
②
③
④
……
多边形面积S
2
2.5
3
4
……
各边上格点的个数和X
4
5
6
8
……
请写出面积S与X之间的关系式为____________________________.
(2)请你再画出一些格点多边形,使这些多边形内部都有且只有2个格点,此时所画的多边形的面积S与它各边上格点的个数和X 之间的关系式为______________ .
(3)请继续探索,当格点多边形内部有且只有n 个格点时,猜想S 与 X 有怎样的关系?
20.(本题满分8分)
某文具店销售的水笔只有A、B、C三种型号,下面表格和统计图分别给出上月这三种型号水笔每支的利润和销售量.
A、B、C三种型号水笔每支的利润统计表:
水笔型号
A
B
C
每支利润(元)
0.6
0.5
1.2
A、B、C三种型号水笔销售量统计图:

(1)分别计算该店上月这三种型号水笔的利润,并将利润分布情况用扇型统计图表示.
(2)若该店计划下月共进这三种型号水笔600支,结合上月销售情况,你认为A、B、C三种型号的水笔各进多少支总利润最高?此时所获总利润是多少?
21.(本题满分10分)
如图,△ABC内接于⊙O,AC=BC,D为⊙O的弧AB上一点,连接DA并延长至E,使CE=CD.
(1)求证:∠ACE=∠BCD
(2)求证:AE=BD
(3)若AC⊥BC,求证:AD+BD=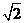 CD
CD

22.(本题满分10分)
如图,A、B为湖滨的两个景点,C为湖心的一个景点,景点B在景点C的正东,从景点A看,点B在北偏东75°方向,景点C在北偏东30°方向.一游客自景点A驾船以每分钟

23.(本题满分10分)
某商场销售某种品牌的饮料,已知进价为每箱40元,生产厂家要求每箱售价在40元~70元之间(可以是40元或70元).市场调查发现,若每箱以50元销售,平均每天可销售90箱,价格每降低1元,平均每天多销售3箱,价格每升高1元,平均每天可少销售3箱。
(1)写出平均每天销售量y (箱)与每箱售价x(元)之间的函数关系式,并指出x的取值范围.
(2)求出商场平均每天销售这种饮料的总利润W(元)与每箱饮料的售价x(元)之间的函数关系式.(利润= 售价-进价)
(3)求出(2)中每箱饮料的售价为多少时,平均每天的总利润最大?最大利润为多少?
24.(本题满分12分)
在△ABC中,AB=AC=2,∠A=90°,O为BC的中点,动点E在AB边上自由移动,动点F在AC边上自由移动.
(1)点E、F移动的过程中,△OEF是否能够成为∠EOF=45°的等腰三角形?若能,请指出△OEF为等腰三角形时动点E、F的位置;若不能,请说明理由.
(2)当∠EOF=45°时,设BE=x,CF=y.求出y与x之间的函数关系式,并写出x的取值范围.
(3)在满足(2)中的条件时,若以O为圆心的圆与AB相切(如图2),试探索直线EF与⊙O的位置关系,并证明你的结论.
