2007-2008学年度临沂市蒙阴县上学期期中考试试题
八年级数学
(时间90分钟,试卷115分+卷面5分,共120分)
一.选择题:相信你一定能选对!(下列各小题的四个选项中,有且只有一个是符合题意的,把你认为符合题意的答案代号选出来,每小题3分,共36分)
1.函数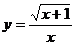 中,自变量
中,自变量 的取值范围是 (
)
的取值范围是 (
)
A. ≥一l B.
≥一l B. >0 C.
>0 C. ≥一l且
≥一l且 ≠0 D.
≠0 D. >一1且
>一1且 ≠0
≠0
2.一次函数 ,若
,若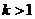 ,则函数图象不经过 ( )
,则函数图象不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图所示,已知AB∥CD,AD//BC,AC与BD交于点O,AE⊥BD于E,CF⊥BD于E,圈中全等三角形有 ( )
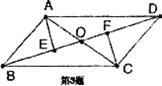
A.3对 B.5对 C.6对 D.7对
4.已知点(一2, l)、(一1,
l)、(一1, 2)、(1,
2)、(1, 3)都在直线
3)都在直线 上,则
上,则 1,
1,  2,
2,  3的值的大小关系是 ( ).
3的值的大小关系是 ( ).
A. 1>
1> 2>
2> 3 B.
3 B. 1<
1< 2<
2< 3 C.
3 C. 3>
3> 1>
1> 2 D.
2 D. 3>
3> 1>
1> 3
3
5.AD是△ABC的角平分线,过点D作DE//AB于E,DF上AC于F,则下列结论不一定正确的是 ( )
A.DE=DF B.BD=CD C.AE=AF D.∠ADE=∠ADF
6.如图,D、E是△ABC中AC、AB上的点,△ADB≌△EDB,△BDE≌△CDE,则下列结论:①AD=DE;②BC=2AB;③∠l=∠2=∠3;④∠4=∠5=∠6.其中正确的有 ( )
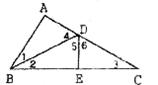
A.4个 B.3个 C.2个 D.1个
7.若一次函数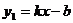 的图象经过第一、二、三、四象限,则一次函数
的图象经过第一、二、三、四象限,则一次函数 的图象经过( )
的图象经过( )
A.第二、三、四象限 B.第一、二、四象限
C.第一、三、图象限 D.第一、二、三象限
8.我班男女生人数之比是3:2,制作扇形统计图时女生对应的扇形的圆心角是 ( )
A.144° B.216° C.72° D.108°
9.下图中两条直线 和
和 和交点坐标可以看作下列方程组中 ( ) 的解.
和交点坐标可以看作下列方程组中 ( ) 的解.

A. B.
B. C.
C. D.
D.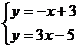
10.已知一次函数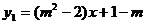 与
与 的图像与
的图像与 轴交点的纵坐标互为相反数,则m的值为 ( )
轴交点的纵坐标互为相反数,则m的值为 ( )
A.一2 B.2 C.一3 D.一4
11.如图是一名同学骑自行车出行的图象,从图象得知正确的信息是( )
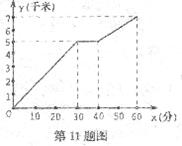
A.整个行进过程中的平均速度是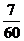 千米/时;B.前20分钟的速度比后半小时速度慢
千米/时;B.前20分钟的速度比后半小时速度慢
C.该同学在途中停下来休息了10分钟; D.从起点到终点该同学共用了50分钟
12.函数 的图像与函数
的图像与函数 的图像平行,且与
的图像平行,且与 轴的交点为M(0,2),则其函数表达式为 ( ).
轴的交点为M(0,2),则其函数表达式为 ( ).
A. B.
B. C.
C. D.
D.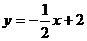
二.填空题:你能填得又对又快吗?(每小题3分,共24分)
13.函数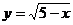 中自变量
中自变量 的取值范围是____________.
的取值范围是____________.
14.分析数据时,为了能清楚地反映事物地变化情况,可以选择____________图;为了能清楚地表示出各部分在总体中所占的百分比,通常选用____________图;而为了能表示出每个项目的具体数目,我们又常选用____________图.
15.△ABC和△A’B’C’,已知AB=A’B’,BC=B’C’,则增加条件_________或________后,△ABC≌△A’B’C’.
16.已知一次函数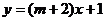 ,函数
,函数 的值随
的值随 值的增大而增大,则m的取值范围是______________.
值的增大而增大,则m的取值范围是______________.
17.函数 =k
=k +b(k≠0)的图象平行于直线
+b(k≠0)的图象平行于直线 =2
=2 +3,且交
+3,且交 轴于点(0,一l),则其解析式是__________.
轴于点(0,一l),则其解析式是__________.
18.已知直线 与坐标轴围成的三角形面积是
与坐标轴围成的三角形面积是 ,则此直线的函数解析式是__________.
,则此直线的函数解析式是__________.
19.小强调查“每人每天的用水量”这一问题时,收集到80个数据,最大数据是70升,最小数据是42升,若取组距为4,则应分为______________组绘制频数分布表.
20.如图把Rt△ABC(∠C=90°)折叠,使A、B两点重合,得到折ED,再沿BE折叠,C点恰好与D点重合,则∠A等于______________度.

三.解答题:一定要细心哟,你也能行的!(共55分)
21.(10分)为了了解某初中学生的体能情况,抽取若干名学生在单位时间内进行引体向上测试,将所得数据整理后,画出频数分布直方图(如图4),图中从左到右依次为第1、2、3、4、5组。

(1) 求抽取多少名学生参加测试?
(2) 处于哪个次数段的学生数最多?(答出是第几组即可)
(3) 若次数在5次(含5次)以上为达标,求这次测试的达标率。
22.(10分)如图, 1反映了甲离开A的时间与离A地的距离的关系,
1反映了甲离开A的时间与离A地的距离的关系, 2反映了乙离开A地的时间与离A地的距离之间的关系,根据图象填空:
2反映了乙离开A地的时间与离A地的距离之间的关系,根据图象填空:

(1)当时间为2小时时,甲离A地________千米,乙离A地________千米。
(2)当时间为6小时时,甲离A地_________米。乙离A地________千米。
(3)当时间________时,甲、乙两人离A地距离相等。
(4)当时间________时,甲在乙的前面,当时间_______时,乙超过了甲。
(5)  1对应的函数表达式为______________,
1对应的函数表达式为______________, 2对应的函数表达式为______________。
2对应的函数表达式为______________。
23.(10分)如图13,在△AFD和△CEB中,点A、E、F、C在同一直线上,有下面四个论断:(1)AD=CB,(2)AE=CF,(3)∠B=∠D,(4)AD//BC.请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出解答过程.

24.(12分)△ABC为正三角形(即AB=AC=BC;∠A=∠B=∠C=60°),点M是射线BC上任意一点,点N是射线CA上任意一点,且BM=CN,直线BN与AM相交于Q点,就下面给出的三种情况,如图8中的①②③,先用量角器分别测量∠BQM的大小,然后猜测∠BQM等于多少度.并利用图③证明你的结论。

25.(13分)我市某乡A,B两村盛产柑桔,A村有柑桔200吨,B村有柑桔300吨.现将这些柑桔运到C,D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨;从A村运往C,D两处的费用分别为每吨20元和25元,从B村运往C,D两处的费用分别为每吨15元和18元。设从A村运往C仓库的柑桔重量为 吨,A、B两村运往两仓库的柑桔运输费用分别为
吨,A、B两村运往两仓库的柑桔运输费用分别为 元和
元和 元.
元.
(1)请填写下表,并求出 、
、 与
与 之间的函数关系式;
之间的函数关系式;
解:
 收地
收地
货运
C
D
总计
A
 吨
吨
200吨
B
300吨
总计
240吨
260吨
500吨
(2)试讨论A,B两村中,哪个村的运费较少;
(3)考虑到B村的经济承受能力,B村的柑桔运费不得超过4830元.在这种情况下,请问怎样调运,才能使两村运费之和最小?求出这个最小值。