2008年浙江省台州八校初中毕业生学业第一次模拟考试
数学试题
一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个正确选项)
1. 今年春节,我市最高气温为
(A)
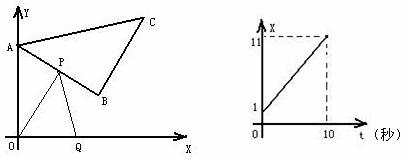
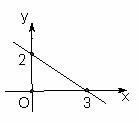
2.一次函数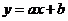 的图象如图所示,则不等式
的图象如图所示,则不等式 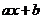 >0的解集是( )
>0的解集是( )
(A)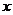 >3 (B)
>3 (B)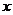 >2 (C)
>2 (C)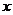 <3
(D)
<3
(D) 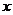 <2
<2
3.随着通讯市场竞争的日益激烈,某品牌的手机价格元旦期间降低了a元,春节前后又下调了25%,该手机现在的价格是b元,则原来的价格是( )
(A) 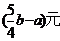 (B)
(B) 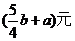 (C)
(C) 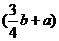 元 (D)
元 (D) 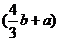 元
元
4.出租车的收费规定:起步价8元,超过
(A)
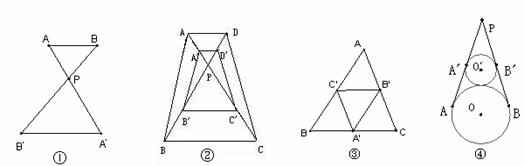
5.下列各组三角形,不全等的是( )

6.某校八(1)班同学上学时乘车,骑车和步行的人数分布直方图和扇形分布图如图所示(两图都不完整),则下列说法错误的是( )
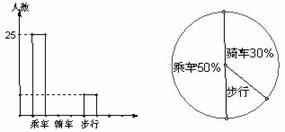
(A) 该班共50人
(B) 该班骑车的有30人
(C) 该班步行的有10人
(D) 该校共有2000名学生,估计骑车上学的约有600人
7.解方程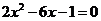 ,王明同学这样解:
,王明同学这样解:
解:方程两边同除以2,并移常数项到右边: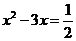 ①
①
方程两边同加上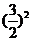 :
:
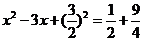 ②
②
即
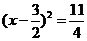 ③
③
方程两边开平方 :
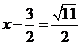 ④
④
∴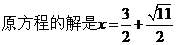
那么下列说法(1)原方程变形成方程①是根据等式的性质;(2)方程①变形成方程②用的是配方法;(3)方程②变形成方程③是根据完全平方公式;(4)方程③变形成方程④出现了错误.其中正确的说法是( )
(A)(1)(2)(3)(4) (B)(2)(3)(4) (C)(3)(4) (D)(4)
8.如图所示的一块长方体木头,沿虚线所示位置截下去所得到的截面图形是( ).




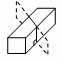 (A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
|
 ,
,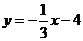 ,
,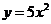 ,
,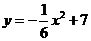 的图象向右平移1个单位,依次得到函数
的图象向右平移1个单位,依次得到函数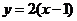 ,
,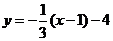 ,
, ,
,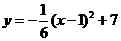 ,那么把函数
,那么把函数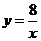 的图象向右平移1个单位,得到的函数是
.
的图象向右平移1个单位,得到的函数是
.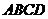 中,AC、BD交于点O,给出下列条件:
中,AC、BD交于点O,给出下列条件: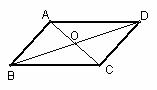
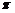 )
)


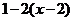 < 0,并把它的解集表示在数轴上.
< 0,并把它的解集表示在数轴上. ,并取一个合适的a的值代入,求出这个代数式的值.
,并取一个合适的a的值代入,求出这个代数式的值.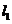 交AB于点E;把△ABC再折叠,使点C与点D重合,折痕
交AB于点E;把△ABC再折叠,使点C与点D重合,折痕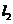 交AC于点F,猜想四边形AEDF是什么特殊的四边形,并证明你的猜想.
交AC于点F,猜想四边形AEDF是什么特殊的四边形,并证明你的猜想.

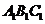 ;
;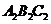 ,使△
,使△ .
. ,
,