2007-2008学年度滨州市滨城区第一学期教学质量检测
八年级数学试题
注意事项:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分。第Ⅰ卷(1~2页)为选择题,共30分;第Ⅱ卷(3~8页)为非选择题,共70分,满分为100分,考试时间为90分钟。
2.答卷时,请务必将自己的学校、姓名、考号等考试信息写在指定位置,选择题选出答案后,一律将其字母标号填在第Ⅱ卷上的第Ⅰ卷答案栏内,不能答在第Ⅰ卷上。
3.考试采用闭卷笔试形式,允许考生使用计算器.
第Ⅰ卷(选择题共30分)
一、选择题:本大题共10小题,每小题3分,计30分.下列各小题所给出的四个答案选项中只有一个是正确的,请你选出来填在第Ⅱ卷上的第Ⅰ卷答案栏内,选对得3分,其它均得零分。
1.下列运算中,计算结果正确的是
(A)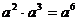 (B)
(B)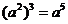
(C)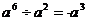 (D)
(D)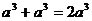
2.函数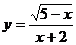 中自变量
中自变量 的取值范围是
的取值范围是
(A) ≥5 (B)
≥5 (B) ≤5且
≤5且 ≠-2
≠-2
(C) ≤5 (D)
≤5 (D) <5上
<5上 ≠-2
≠-2
3.如图,E,B,F,C四点在一条直线上EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是
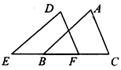
(A)AB =DE (B)DF∥AC (C)∠E=∠ABC (D)AB∥DE
4.要直观地反映出某种股票的涨跌情况,应选择
(A)条形的统计图 (B)扇形的统计图
(C)折线的统计图 (D)直方图
5.点A(-3,4)关于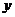 轴对称的点的坐标为
轴对称的点的坐标为
(A)(3,-4) (B)(3,4) (C)(-3,-4) (D)(-3,4)
6.下列多项式中,不能进行因式分解的是
(A)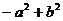 (B)
(B)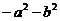
(C)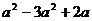 (D)
(D)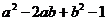
7.如图,△ABC的边AB的垂直平分线分别交BC、AB于点D、E,AE=
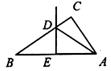
(A)
8.等腰但不等边的三角形的角平分线、高线、中线的总条数是
(A)3 (B)5 (C)7 (D)9
9.△ABC的三边a、b、c满足: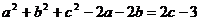 ,则△ABC为
,则△ABC为
(A)直角三角形 (B)等腰直角三角形
(C)等腰三角形 (D)等边三角形
10.如图所示,一次函数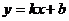 的图象经过A、B点,则
的图象经过A、B点,则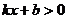 的解集是
的解集是
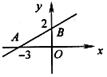
(A) >0
(B)
>0
(B) >2 (C)
>2 (C) >-3 (D)-3<
>-3 (D)-3< <2
<2
第Ⅱ卷(非选择题 共70分)
二、本大题共10个小题,每小题3分,计30分。只要求填写最后结果,不写中间过程。
11.若三角形三个内角的度数之比为1∶2∶3,最短的边长是
12.一个一次函数的图象与直线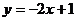 平行,且经过点(2,-1),则这个一次函数的表达示为 。
平行,且经过点(2,-1),则这个一次函数的表达示为 。
13.一组数据共50个,分为6组,其中第一组有6个数据,则该组的频率是 ;第二、三、四、五小组的频率为0.1,0.24,0.18,0.20,则第六小组有 个数据。
14.如图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形。
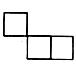
15.请你写出一个二次三项式,使得二次项系数为3, 。
16.等腰三角形的一个外角是110°,则它的顶角和底角的度数分别是 。
17:已知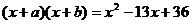 ,则
,则 的值是
。
的值是
。
18.直线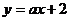 和直线
和直线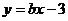 的交点在
的交点在 轴上,则a与b的比值是
。
轴上,则a与b的比值是
。
19.如下图,点P是∠BAC的平分线上一点,PE⊥AB,PF⊥AC,E、F分别为垂足,①PE=PF,②AE=AF,③∠APE=∠APF,上述结论中正确的是 (只填序号)。
20.已知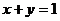 ,则
,则 。
。
三、本大题共5个小题,计40分。解答要求写出文字说明或推演过程。
21.(本小题满分6分)
对于实数a、b、c、d我们规定一种运算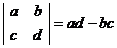 ,如
,如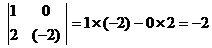 。请先化简式子
。请先化简式子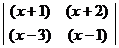 ,再求该式当
,再求该式当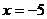 时的值。
时的值。
22.(本小题满分6分)
如图所示,在△ABD和△ACE中,F、G分别是AC和DB、AB和CE的交点,给出以下4个论断:①AB=AC;②AD=AE;③AF=AG;④AD⊥BD,AE⊥CE,以其中3个论断为题设,填入下面的“已知”栏中,1个论断为结论,填入下面的“求证”栏中,使之组成一个真命题,并写出证明过程。
已知: ;
求证:

23.(本小题满分8分)
据

(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?
24.(本小题满分10分)
为调动销售人员的积极性,A、B两公司采取如下工资支付方式:A公司每月2000元基本工资,另加销售额的2%作为奖金;B公司每月1600元基本工资,另加销售额的4%作为奖金。已知A、B公司两位销售员小李、小张1―6月份的销售额如下表:
月份
销售额
销售额(单位:元)
1月
2月
3月
4月
5月
6月
小李(A公司)
11600
12800
14000
15200
16400
17600
小张(B公司)
7400
9200
11000
12800
14600
16400
(1)请问小李与小张3月份的工资各是多少?
(2)小李1~6月份的销售额 与月份
与月份 的函数关系式是
的函数关系式是 ,小张1~6月份的销售额
,小张1~6月份的销售额 也是月份
也是月份 的一次函数,请求出
的一次函数,请求出 与
与 的函数关系式;
的函数关系式;
(3)如果7~12月份两人的销售额也分别满足(2)中两个一次函数的关系,问几月份起小张的工资高于小李的工资。
25.(本小题满分10分)
在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明);
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
