2007-2008学年度滨州市滨城区第一学期教学质量检测
九年级数学试题
第Ⅰ卷(选择题 共30分)
一、选择题:本大题共10小题,每小题3分,计30分。下列各小题所给出的四个答案选项中只有一个是正确的,选对得3分,其它均得零分。
1.下列计算正确的是
A.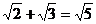 B.
B.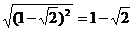
C.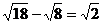 D.
D.
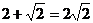
2.下列图案中,不能由一个图形通过旋转而形成的是
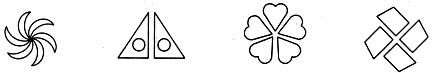
A B C D
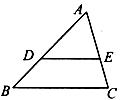
3.如下图,在△ABC中,DE//BC,且S△ABC =S四边形DBCE,若AD=1+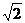 ,则DB=
,则DB=
A. 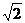 B.
B. 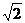 一
一
4.某种药品经过两次降价,从原来的每箱60元降为每箱38.4元,平均每次降价率为
A. 10% B. 15% C. 20% D. 30%
5.四张完全相同的卡片上,分别画有圆、矩形、等边三角形、等腰梯形,现从中随机抽取一张,卡片上画的恰好是中心对称图形的概率是
A. 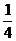 B.
B.
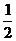 C.
C.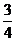 D. 1
D. 1
6.如图.在直径为
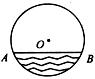
A.
7.如图,小正方形的边长均为1,则下列图中的阴影三角形与△ABC相似的是

A B C D
8.如图PA、PB切⊙O于点A、B,点C是⊙O上一点,且∠ACB=65°,则∠P的度数是
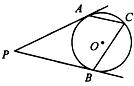
A. 50° B. 60° C. 65° D. 70°
9.函数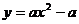 与
与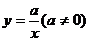 在同一直角坐标系中的图象可能是
在同一直角坐标系中的图象可能是

A B C D
10.如图,在直角梯形ABCD中,∠A=∠B=90°,AB=13,AD=2,BC=6,如果AB上的点P使得以P、A、D为顶点的三角形和以P、B、C为顶点的三角形相似,则这样的点P有
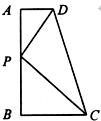
A. 1个 B. 2个 C. 3个 D. 4个
第Ⅱ卷 非选择题 共70分
二、本大题共l0个小题,每小题3分,计30分.只要求填写最后结果,不写中间过程.
11. 若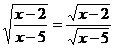 成立,则
成立,则 应满足的条件是_______________________.
应满足的条件是_______________________.
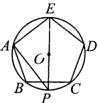
12. 如图,⊙O是正五边形ABCDE的外接圆,PE是⊙O的直径,则∠AEP= ___________.
13. 计算: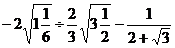 =_____________________________。
=_____________________________。
14.若关于 的方程
的方程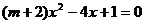 有两个实数根,则m应满足的条件是__________.
有两个实数根,则m应满足的条件是__________.
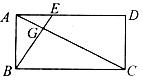
15. 如图,在矩形ABCD中,点E是AD上一点,县AE:ED=1:2,BE与AC相交于点G,则S△BCG:S四边形CDEG=______________.
16.若菱形的两条对角线长的和是
17.如图,半径为1的三个圆两两外切,阴影部分的面积为______________.结果保留根号.

18.把尺寸完全相同但画面不同的两张扑克牌都从中间剪断,再把4张相同的小图片混合在一起.从4张图片中随机地摸取一张,接着再随机地摸取一张.则两张小图片恰好能合成一张完整的扑克牌的概率是__________________.
19.开口向上的抛物线 经过点A(-2,0),B(1,0),则不等式
经过点A(-2,0),B(1,0),则不等式 的解集是_____________________.
的解集是_____________________.
20.手工课上小明遇到这样一个难题:要把一个无盖的单位正方体的展开图剪开拼成一个正方形图案,不准有缝隙也不能有剩余.请你在图①中帮他画出剪的方案,在右边方框中画出拼的方案.


(本小题满分6分)
三、本大题共5个小题,计40分.解答要求写出文字说明或推演过程.
21.用配方法解方程:
(本小题满分6分)
22.如图,在△ABC中,∠BAC=90°,BC的垂线交BC于点D,交AC于点E,交BA的延长线于点F
(1).写出图中与△AEF相似的所有三角形不必说明理由.
(2).求证:BD?DC=DE?DF

(本小题满分8分)
23.某工厂的大门是由上面的抛物线AED和下面的矩形ABCD构成,矩形的长BC为
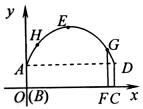
(1). 求矩形的宽AB.
(2). 抛物线上的点H处的灯泡己坏,点H到AB的水平距离为
(本小题满分10分)
24. 如图,在△AEF中,AG平分∠EAF,其延长线交△AEF的外接圆⊙O于点D,过点D作EF的平行线交AE,AF的延长线于B,C两点。
求证:1. BC为⊙O的切线.
2. 连结FD,若AG=9,FD=6,求DG的长.

(本小题满分l0分)
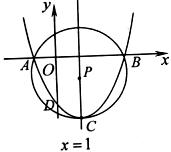
25.如图,对称轴为直线 =1的抛物线
=1的抛物线 与
与 轴交于A、B两点,与y轴交于点D(0,-2),点P在抛物线对称轴上并且位于
轴交于A、B两点,与y轴交于点D(0,-2),点P在抛物线对称轴上并且位于 轴的下方,以点P为圆心作过A、B两点的圆,恰好使得
轴的下方,以点P为圆心作过A、B两点的圆,恰好使得 的长为⊙P周长的
的长为⊙P周长的 .
.
1. 求该抛物线的解析式.
2. 求⊙P的半径和圆心P的坐标,并判断抛物线的顶点C与⊙P的位置关系.
3. 在抛物线上是否存在一点M使得S△ABM= ?若存在,求出所有符合条件的点M的坐标.若不存在,请说明理由.
?若存在,求出所有符合条件的点M的坐标.若不存在,请说明理由.