2007-2008学年度德州市陵县第一学期期中考试
九年级数学试题
一、选择题(每小题3分,共24分)
1.小明的作业本上有以下四题:①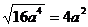 ,②
,② ,③
,③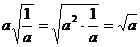 ,④
,④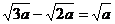 ,做错的题是( )
,做错的题是( )
A.① B.② C.③ D.④
2.方程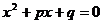 的根是
的根是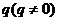 ,则
,则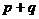 的值等于(
)
的值等于(
)
A.-1 B.
3.图中所列图形中,是中心对称图形的是( )
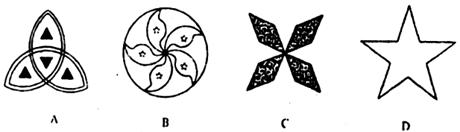
4.在一个暗箱里放入除颜色外,其他都相同的3个红球和11个黄球,搅拌均匀后随机任取一个球,取到红球的概率是( )
A.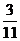 B.
B. C.
C. D.
D.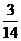
5.若两圆圆心距为4,两圆半径长分别为方程 的两根。则这两圆的位置关系是( )
的两根。则这两圆的位置关系是( )
A.相离 B.外切 C.相交 D.内切
6.某校计划在校园内修建一座周长为l
A.正三角形 B.正方形 C.圆 D.不能确定
7.如下图(1),在正方形铁板上剪下一个圆形和扇形,使之恰好围成图(2)所示的一个圆锥模型,设圆的半径为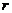 ,扇形半径为
,扇形半径为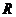 ,则圆的半径与扇形半径之间的关系为( )
,则圆的半径与扇形半径之间的关系为( )

A.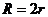 B.
B. C.
C.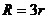 D.
D.
8.如图,半圆O的直径AB=4,与半圆O内切的动圈O1与AB切于点M,设⊙O1的半径为 , AM=
, AM= ,则
,则 关于
关于 的函数关系式是(
)
的函数关系式是(
)

A.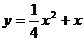 B.
B.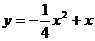
C.  D.
D.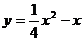
二、填空题(每题3分,共24分)
9.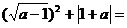 _________。
_________。
10.已知关于 的一元二次方程
的一元二次方程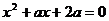 的一个根是2, 则另一根为_________。
的一个根是2, 则另一根为_________。
11.如果方程 有实数根,那么
有实数根,那么 的取值范围是_________。
的取值范围是_________。
12.若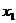 、
、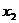 是一元二次方程
是一元二次方程 的两根,则
的两根,则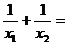 _________。
_________。
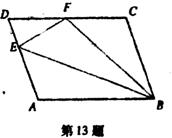
13.如图平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为8,△FCB的周长为22,则FC的长为_________。
14.已知M(1,2),以M为圆心作圆,与坐标轴相交有且只有三个交点,则⊙M的半径为_________。
15.在Rt△ABC中,∠C=90°,AC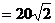 ,BC=10,以AC为轴旋转一周得到一个圆锥,则这个圆锥侧面展开图的圆心角等于_________度。
,BC=10,以AC为轴旋转一周得到一个圆锥,则这个圆锥侧面展开图的圆心角等于_________度。
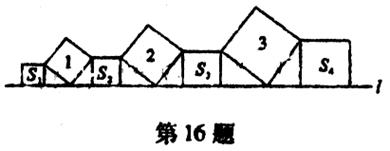
16.在直线 上依次摆放着七个正方形(如图),已知斜放置的三个正方形的面积分别是1、2、3.正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_________。
上依次摆放着七个正方形(如图),已知斜放置的三个正方形的面积分别是1、2、3.正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_________。
三、解答题(共72分)
17.计算(7分)
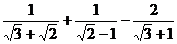
18.用配方法解方程(7分)
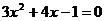
19.当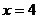 时,求
时,求 的值。(8分)
的值。(8分)
20.(10分)
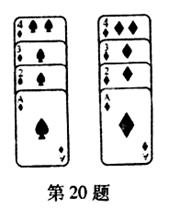
如图是从一副扑克牌中取出的两组牌,分别是黑桃A(表示字1),2,3,4和方块A(表示数字l),2,3,4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌的牌面数字之和等于5的概率是多少?请你用列举法(列表或画树形图)加以分析说明。
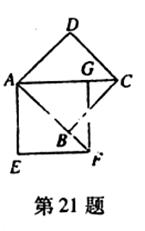
21.(8分)如图,正方形ABCD经旋转后能与正方形AEFG重合,哪一点是旋转中心?旋转的角度是多少度?点D、C、B的对应点分别是哪个点?线段BC和线段AC的对应线段分别是哪条线段?
22.(10分)是否存在一个非负整数 ,使关于
,使关于 的一元二次方程
的一元二次方程 有两个实数根?若存在,请写出
有两个实数根?若存在,请写出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
23.(10分)如图所示,AB是⊙O的直径,点D在AB的延长线上,且DB=BO,过点A作弦AC,使∠CAB=30°,连结DC,DC是⊙O的切线吗?为什么?

24.(12分)圆心角都是90°的扇形OAB与扇形OCD,如图所示叠放在一起,连结AC、BD。
(1)求证:△AOC≌△BOD
(2)若OA=
