2006-2007年滨州市博兴区第二学期期末考试
八年级数学试题
(I卷,此卷不交)
一、选择题(每小题3分,共45分。选出唯一正确答案的代号填在II卷的答题栏内)
1.化简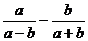 等于
等于
A、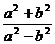 B、
B、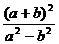
C、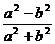 D、
D、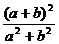
2.某件工作,甲单独做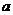 小时完成,乙单独做
小时完成,乙单独做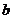 小时完成,则甲、乙两人合作完成需要小时数为
小时完成,则甲、乙两人合作完成需要小时数为
A、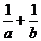 B、
B、 C、
C、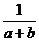 D、
D、
3.下列命题中不成立是
A、三个角的度数之比为l:3:4的三角形是直角三角形
B、三个角的度数之比为1: :2的三角形是直角三角形
:2的三角形是直角三角形
C、二三边长度之比为l: :2的三角形是直角三角形
:2的三角形是直角三角形
D、三边长度之比为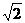 :
: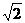 :2的三角形是直角三角形
:2的三角形是直角三角形
4.如图,点A是反比例函数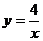 的图像上一点,AB⊥
的图像上一点,AB⊥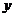 轴于点B,则△AOB的面积是
轴于点B,则△AOB的面积是

A、1 B、2 C、3 D、4
5.用配方法解下列方程,其中应在左右两边同时加上4的方程是
A、 B、
B、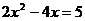
C、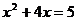 D、
D、
6.一组对边平行,并且对角线互相垂直且相等的四边形是
A、菱形或矩形 B、正方形或等腰梯形
C、矩形或等腰梯形 D、菱形或直角梯形
7.观察图形,判断 与
与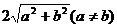 的大小
的大小

A.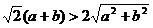 B.
B.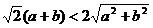
C. D.
D. 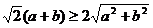
8.如图,E、F、G、H分别是四边形ABCD四条边的中点,要使四边形EFGH为矩形,四边形ABCD应具备的条件是
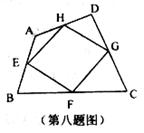
A、一组对边平行而另一组对边不平行 B、对角线相等
C、对角线互相垂直 D、对角线互相平分
9.如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是
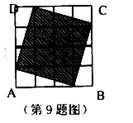
A、3∶4 B、5∶8 C、9∶16 D、1∶2
10.四边形ABCD的对角线相交于点O,给出下列条件:
①AB∥CD ② AD∥BC ③ AB=CD ④∠BAD=∠DCB
从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有
A、6组 B、5组 C、4组 D、3组
11.若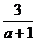 表示一个整数,则整数
表示一个整数,则整数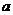 可以值有
可以值有
A、1个 B、2个 C、3个 D、4个
12.如图,正方形硬纸片ABCD的边长是4,点E、F分别是AB、BC的中点,若沿左图中的虚线剪开,拼成如下右图的一座“小别墅”,则图中阴影部分的面积是
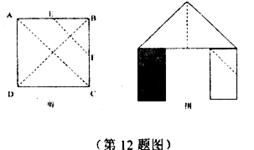
A、2 B、4 C、8 D、10
13.若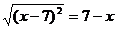 ,则
,则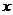 的取值范围是
的取值范围是
A、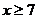 B、
B、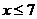 C、
C、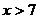 D、
D、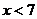
14.当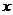 取某一范围的实数时,
取某一范围的实数时, 的值是一个常数,则该常数是
的值是一个常数,则该常数是
A、29 B、16 C、13 D、3
15.若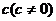 为关于
为关于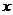 的一元二次方程
的一元二次方程 的根,则
的根,则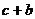 的值为
的值为
A、1 B、-1 C、2 D、-2
二、填空题(每小题4分,共20分,把正确答案填在II卷的答题栏内)
16.使式子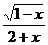 有意义的
有意义的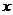 的取值范围是_____________。
的取值范围是_____________。
17.一个两位数,个位数字比十位数字大3,个位数字的平方刚好等于这个两位数,则这个两位数为_____________。
18.已知正比例函数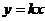 的图像与函数
的图像与函数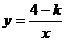 的图像有一个交点的横坐标是-1,那么它们的交点坐标分别为_____________。
的图像有一个交点的横坐标是-1,那么它们的交点坐标分别为_____________。
19.矩形的顶点A、B、C、D按顺时针方向排列,若在平面直角坐标系内B、D两点对应的坐标分别是(2,0),(0,0),且A、C两点关于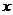 轴对称,则C点对应的坐标是_____________。
轴对称,则C点对应的坐标是_____________。
20.不改变分式的值,将分式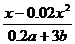 中各项系数均化为整数,则最简结果为_____________。
中各项系数均化为整数,则最简结果为_____________。
(II卷,答题卷)
三、解答题(共55分)
21.(5分)计算: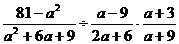
22.(5分)计算: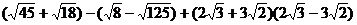
23.(5分)解方程: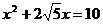
24.(6分)在平面直角坐标系中,点A到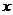 轴的距离为AB=2,且OA与
轴的距离为AB=2,且OA与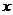 轴的正方向为
轴的正方向为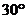 ,若反比例函数经过点A,且在每一个象限内
,若反比例函数经过点A,且在每一个象限内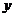 随
随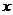 的增大而减小。试求反比例函数的解析式。
的增大而减小。试求反比例函数的解析式。
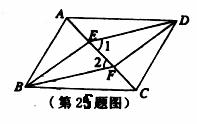
25.(8分)如图,ABCD是平行四边形,BE∥DF,分别交对角线AC于E、F,连接ED、BF。求证∠l=∠2。
26、(8分)两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月才全部完成。哪个队的施工速度快?
27.(8分)有一人患了流感,经过两轮传染后共有l21人患了流感。
(1)每轮传染中平均一个人传染了几个人?
(2)三轮传染后有多少人患流感?
28.(10分)如图,四边形ABCD是直角梯形,∠B=90°,AB=
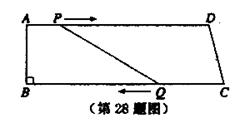
(1)四边形PQCD成为平行四边形?
(2)四边形PQCD成为等腰梯形?
(3)四边形BAPQ与CDPQ的面积相等?