2006-2007学年度德州市陵县第二学期八年级期末考试
数学试题
一、选择题:(每小题3分,共30分)
1.如果分式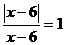 的值为l,则
的值为l,则 的值为( )
的值为( )
A. ≥0 B.
≥0 B. >6
C.
>6
C. ≥0且
≥0且 ≠6 D.
≠6 D. ≠6
≠6
2.若 =1是分式方程
=1是分式方程 的解,则
的解,则 的值为( )
的值为( )
A.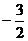 B.1 C.
B.1 C.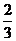 D.
D.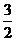
3.在函数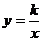 的图象上有三点A(-2,
的图象上有三点A(-2,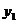 ),B(-l,
),B(-l,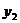 ),C(2,
),C(2,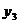 )则
)则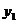 、
、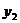 、
、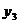 的大小关系是( )
的大小关系是( )
A.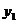 >
>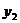 >
>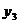 B.
B.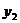 >
>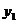 >
>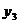 C.
C.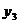 >
>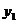 >
>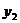 D.以上都不正确
D.以上都不正确
4.下列命题正确的个数为( )
①两条对角线互相垂直的矩形是正方形
②正方形是特殊的矩形
③正方形有4条对称轴
④对角线相互垂直的四边形是菱形
⑤矩形的两条对角线相互垂直平分
A.1个 B.2个 C.3个 D.4个
5.已知三角形的三边分别为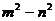 ,
, ,
,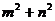 (
(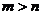 ,
, 、
、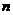 是正整数),则此三角形为( )
是正整数),则此三角形为( )
A.直角三角形 B.等腰直角三角形 C.锐角三角形 D.钝角三角形
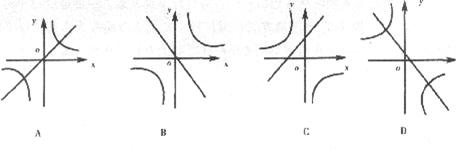
6.若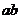 <0,则函数
<0,则函数 与
与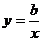 在同一平面直角坐标系中的图象大致是( )
在同一平面直角坐标系中的图象大致是( )
7.如图1□ABCD的周长为l6cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
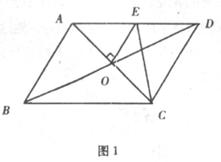
A.4cm B.6cm C.8cm D.10cm
8.已知一组数据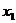 、
、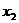 、
、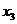 、
、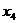 、
、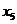 的平均数为2,方差为
的平均数为2,方差为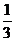 ,那么另一组数据
,那么另一组数据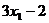 ,
,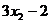 ,
,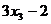 ,
,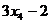 ,
, 的平均数和方差是( )
的平均数和方差是( )
A.2,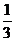 B.2,l C.4,
B.2,l C.4,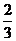 D.4,3
D.4,3
9.如图2正比例函数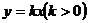 与反比例函数
与反比例函数 的图象相交于A、C两点,过A作
的图象相交于A、C两点,过A作 轴的垂线交
轴的垂线交 轴于B,连结
轴于B,连结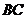 若
若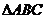 的面积为S。那么( )
的面积为S。那么( )
A.S=1 B.S=2 C.S=3 D.不能确定

10.如图3,先对折矩形得折痕MN,再折纸使折线过点B,且使得A在MN上,这时折线EB与BC所成的角为( )
A.30° B.45° C.60° D.75°
二、填空题(每小题3分,共30分)
11.已知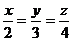 ,那么
,那么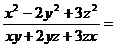 ____________
____________
12.若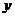 与
与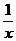 成反比例,
成反比例, 与
与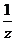 成正比例,则
成正比例,则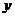 是
是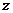 的__________函数。
的__________函数。
13.已知甲、乙、丙、丁四支足球队在世界杯预选赛中进球数分别为:9,9, ,7,若这组数据的众数与平均数恰好相等。则这组数据的中位数是__________。
,7,若这组数据的众数与平均数恰好相等。则这组数据的中位数是__________。
14.已知 为整数,且分式
为整数,且分式 的值为整数,则
的值为整数,则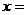 __________。
__________。
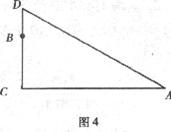
15.如图4.在一棵树的10米高的B处有两只猴子,一只猴子爬下树走到离树20米处的A处,另一只爬到树顶D后顺绳子滑到A处,如果两只猴子所经过的距离相等,则这棵树高____米。
16.已知△ABC的a、b两边分别为9,40,另一边c为奇数,且a+b+c是3的倍数,则c应为__________。
17.若等腰梯形的三边长分别为3,4,11,则这个等腰梯形的周长是__________。
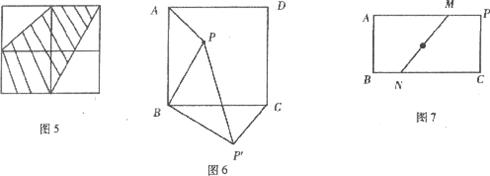
18.如图5,大正方形是由四个边长为1的相同的小正方形组成的,则图中阴影部分的面积为__________。
19.如图6,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转,能与△CBP′重合,若PB=3,则PP′=__________。
20.如图7,ABCD是一张矩形纸片,点O为矩形对角线的交点,直线MN经过点O交AD于M,交BC于N,操作先沿直线MN剪开,并将直角梯形MNCD绕点O旋转__________度后(填入一个你认为正确的序号;①90°②l80°③270°④360°),恰与直角梯形NMAB完全重合,再将重合后的直角梯形MNCD以直线MN为轴翻转l80°后所得到的图形是下列中的____(填写正确图形的代号)

三、解答题(60分)
21.(8分)已知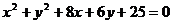
求: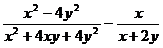 的值.
的值.
22.(8分)某市举行一次少年滑冰比赛,各年龄组的参赛人数如下表所示:
年龄组
13岁
14岁
15岁
16岁
参赛人数
5
19
12
14
(1)求全体参赛选手年龄的众数、中位数;
(2)小明说他所在年龄组的参赛人数占全体参赛人数的28%.你认为小明是哪个年龄组的选手?请说明理由.
23.(10分)如图8,在口ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点
求证:(1)BE⊥AC
(2)EG=EF

24.(10分)甲乙二人同时从A地出发,各骑自行车到B地,甲的速度每小时比乙快2千米,甲到达距A地36千米的地方时,因自行车发生故障而改为步行,每小时速度比原来减少8千米,结果两人恰好都用4小时同时到达8地,求两人骑车的速度各为多少?
25.(12分)已知一次函数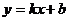 的图象与反比例函数
的图象与反比例函数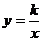 的图象相交于点P(2,1),与
的图象相交于点P(2,1),与 轴交于点E,与y轴交于点F,O为坐标原点.
轴交于点E,与y轴交于点F,O为坐标原点.
(1)求k,b的值;
(2)在同一坐标系中画出这两个函数的图象;
(3)△EOF的面积是△EOP的面积的多少倍?
(4)能不能在反比例函数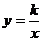 的图象上找到一点Q,使△QOE的面积和△EOF面积相等.如果能,请写出Q点的坐标;如果不能,请说明理由.
的图象上找到一点Q,使△QOE的面积和△EOF面积相等.如果能,请写出Q点的坐标;如果不能,请说明理由.
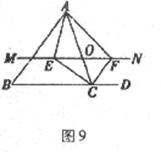
26.(12分)如图9所示,△ABC中,点O是AC边上的一个动点,过点O作直线MN//BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)在(2)的条件下,再添加一个什么条件,四边形AECF是正方形?(不需证明)