2007年滨州市阳信县第二学期期末质量检测
初二数学试卷
一.选择题(每小题3分.共30分)
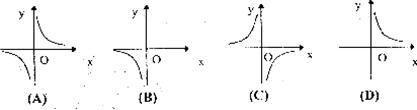
1.下列函数中,属于反比函数的是( )
(A)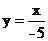 (B)
(B) 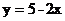 (C)
(C) (D)
(D)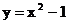
2、某鞋店试销一种新款式女鞋,试销期间的销量情况如下表所示.
尺码(厘米)
22
23
24
25
销售量(双)
3
12
8
2
对这个鞋店的经理来说,他关心哪种尺码鞋最畅销,则下列统计量对鞋店经理来说最重要的是( )
(A)平均数 (B)中位数
(C)众数 (D)以上说法均不对
3.下列几组数中,不能作为直角三角形三边长度的是( )
(A)a=7,b=24,c=25 (B)a= 1.5,b=2,c=2.5
(C)a=2/3,b=2,c=5/4 (D)a=l5,b=8,c=17
4.下列各式: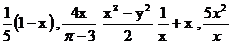 等,其中分式共有( )个。
等,其中分式共有( )个。
(A)2 (B) 3 (C)4 (D)5
5.若等腰三角形中,相等的两边长为lOcm,第三边长为l
(A)
6.如图(1),平行四边形ABCD中,∠A的平分线AF交DC于E,AB=5,BC=3,则EC的长( )
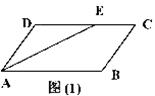
(A)1 (B)1.5 (C)2 (D)3
7.已知一个矩形的面积为
8.如果把分式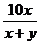 中的x、y都扩大l0倍,则分式的值是( )
中的x、y都扩大l0倍,则分式的值是( )
(A)扩大l00倍 (B)扩大l0倍
(C)不变 (D)缩小到原来的1/10
9.如图(3),点A是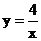 图象上一点,
图象上一点, 轴于点B则△AOB的面积是( )
轴于点B则△AOB的面积是( )
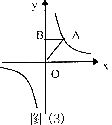
(A)1 (B)2 (C)3 (D)4
10.如图(4),在平行四边形ABCD中,∠B=l10°,延长AD至F,延长CD至E连结EF,则∠E+∠F=( )
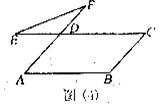
(A) 110° (B)30° (C)50° (D)70°
二.填空(每小题:3分,共36分)
11.当x 时,分式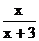 有意义.
有意义.
12.将方程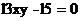 改写成y是x的函数关系是______________.
改写成y是x的函数关系是______________.
13.一组同学身高的极差为
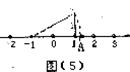
14.如图(5),数轴上点A所表示的数为a,则a的值是 .
15.若分式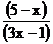 的值是2,则x=______________.
的值是2,则x=______________.
16.若反比例函数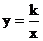 的图象经过点(-2,1),则在x>0,或 x<0.时,y随x的增大而______________.
的图象经过点(-2,1),则在x>0,或 x<0.时,y随x的增大而______________.
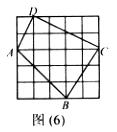
17.如图(6),小方格都是边长为1的正方形,则四边形ABCD面积是 _________.
18.矩形的两条对角线的夹角为60°,较短的边长为
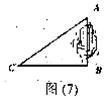
19.如图(7),隔湖有两点A、B,从BA方向成直角的BC方向上的点C ,测得:CA=
20.已知一组数据1,-2,-l,0,2,l,0,-l这组数据的方差为______.
21.已知菱形的一条对角线长为
22.在实数范围内定义一种运算“※",其规则为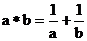 ,根据这个规则方程
,根据这个规则方程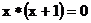 的解为____________.
的解为____________.
三.解答题:本大题共7小题,共54分.解答应写出文字说明、证明过程或演算步骤.
23.先化简代数式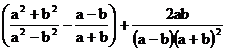 ,然后请选择一组你喜欢的a,b的值代入求值。(6分)
,然后请选择一组你喜欢的a,b的值代入求值。(6分)
24.我县自来水厂为了了解某小区居民的用水情况;随机抽查了该小区l0户家庭的月用水量,结果如下:
月用水量(立方米)
17
lO
14
13
18
户 数
2
2
3
2
1
(1)计算这10户家庭该月的平均用水量;
(2)如果该小区有450户家庭,根据上面的计算结果,估计该小区居民每月共用水多少立方米? (8分)
25.已知变量y与x成反比例,并且当x=2时,y=-3
(1)求y与x的函数表达式;
(2)求y=2时,x的值;
(3)画出函数图象的草图. (6分)
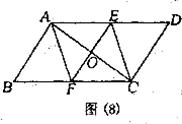
26.如图(8),在平行四边形ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F.
试猜想:四边形AFCE形状,并证明你的猜想. (8分)
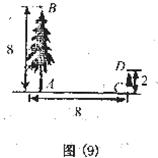
27.如图(9),有两棵树,一棵高
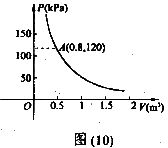
28.某气球内充满了一定质量的气体,当温度不变时.气球随气体的气压p(kPa)是体积V(m3)的反比例函数:其图象如图(10)所示.
(1)写出这一函数表达式:
(2)当气体体积为lm3时,气压为多少?
(3)当气球内得气压大于140 kPa时,气球将会爆炸.为了安全起见,气体的体积应不少于多少? (9分)
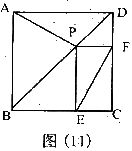
29.如图(11),在正方形ABCD中,P为对角线BD上一_点,PE⊥BC垂足为E,PF⊥CD, 垂足为 F 求证:EF=AP (9分)