2007年丰台区初三统一练习(一)
数 学 试 卷
考生须知
1.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共10页。
2.认真填写密封线内的学校、姓名和报名号。
第 Ⅰ 卷 (选择题 32分)
注意事项
1.考生要按要求在机读答题卡上作答,题号要对应,填涂要规范。
2.考试结束,将试卷和机读答题卡一并交回。
一、选择题(共8个小题,每小题4分,共32分)在每个小题给出的四个备选答案中,只有一个是符合题目要求的.
1. -5的绝对值是
A. 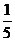 B.
-
B.
-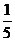 C. 5
D. -5
C. 5
D. -5
2. 废电池是一种危害严重的污染源,一粒纽扣电池可以污染600
A. 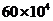 升 B.
升 B. 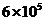 升 C.
升 C. 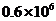 升
D.
升
D. 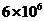 升
升
3. 在函数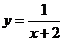 中,自变量x的取值范围是
中,自变量x的取值范围是
A.  B.
B. 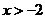 C.
C.
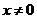 D.
D.

4. 如图,是一个物体的三视图,则该物体的形状是

A. 圆锥 B.圆柱 C. 三棱锥 D. 三棱柱
5. 某鞋店试销一种新款运动鞋,试销期间销售情况如下表:
型 号
22
22.5
23
23.5
24
24.5
25
数量(双)
3
5
10
15
8
3
2
对于这个鞋店的经理来说最关心的是哪种型号的鞋畅销,则下列统计量对鞋店经理来说最有意义的是
A. 平均数 B. 众数 C. 中位数 D. 标准差
 6. 小明用作函数图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数图象l1、l2 如图所示,他解的这个方程组是
6. 小明用作函数图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数图象l1、l2 如图所示,他解的这个方程组是
A. 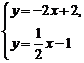 B.
B.
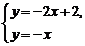
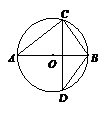 C.
C. 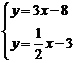 D.
D.
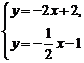
7. 如图, AB是⊙O的直径, CD是弦, 且CD⊥AB, 若BC=6,
AC=8, 则sin∠ABD的值为
A. 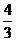 B.
B.
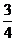 C.
C.
 D.
D.

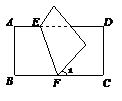 8. 如图,把矩形ABCD沿EF对折,若∠1=
8. 如图,把矩形ABCD沿EF对折,若∠1= ,则∠AEF等于
,则∠AEF等于
A.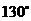 B.
B.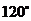
C.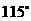 D.
D.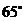
第Ⅱ卷 (非选择题 88分)
注意事项
1.第Ⅱ卷包括七道大题,考生一律用蓝色或黑色钢笔、圆珠笔在试卷上按题意和要求作答。
2.字迹要工整,卷面要整洁。
题 号
二
三
四
五
六
七
八
总 分
分 数
阅卷人
复查人
得分
阅卷人
二、填空题(共4个小题 , 每小题4分,共16分)
9. 点A(-1,y1),B(-2,y2)在双曲线 上, 则y1与y2的大小关系是____________.
上, 则y1与y2的大小关系是____________.
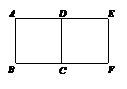 10. 有四张不透明的卡片,正面分别写有:
10. 有四张不透明的卡片,正面分别写有: ,
,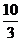 , -2,
, -2, 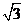 . 除正面的数不同外,其余都相同.将它们背面朝上洗匀后.从中随机抽取一张卡片,抽到写有无理数的卡片的概率是__________.
. 除正面的数不同外,其余都相同.将它们背面朝上洗匀后.从中随机抽取一张卡片,抽到写有无理数的卡片的概率是__________.
11. 如图,若正方形DCFE旋转后能与正方形ABCD重合,那么
图形所在平面上可以作为旋转中心的点有_______个.
12. 对于整数a、b、c、d规定符号 ,若
,若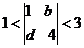 ,则b+d=_______.
,则b+d=_______.
得分
阅卷人
三、(共3个小题,其中13小题4分,14、15小题每小题5分,共14分)
13.
分解因式: . 14. 计算:
. 14. 计算: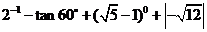 .
.
解: 解:
15.
解方程: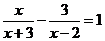 .
.
解:
得分
阅卷人
四、(共4个小题, 每小题5分,共20分)
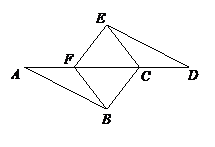 16. 已知:如图,AB∥DE,
AB=DE,
AF=DC.
16. 已知:如图,AB∥DE,
AB=DE,
AF=DC.
(1) 写出图中你认为全等的三角形(不再添加辅助线);
(2)选择你在(1)中写出的全等三角形中的任意一对进行证明.
(1)全等三角形有_______________________________;
(2) 求证:________________________.
证明:
17.已知关于x的一元二次方程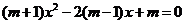 有实数根,求m的取值范围.
有实数根,求m的取值范围.
解:
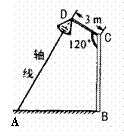 18. 如图,要在宽为
18. 如图,要在宽为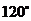 角,路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直.当灯罩的轴线通过公路路面的中线时,照明效果最理想.问:应设计多高的灯柱,才能取得最理想的照明效果(精确到0.01).
角,路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直.当灯罩的轴线通过公路路面的中线时,照明效果最理想.问:应设计多高的灯柱,才能取得最理想的照明效果(精确到0.01).
解:
19. 已知:如图,AB是⊙O的直径, ⊙O过BC的中点D,且DE⊥AC于点E.
 (1)求证:DE是⊙O的切线;
(1)求证:DE是⊙O的切线;
(2)若∠C=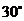 , CD=
, CD=
(1)证明:
(2)解:
得分
阅卷人
五、(共3个小题,每小题5分,共15分)
20. 如图,矩形纸片ABCD是由24个边长为1的正方形排列而成, M是AD的中点.
(1)沿虚线MB剪开,分成两块纸片进行拼图.
要求: ①拼成直角三角形; ②拼成平行四边形; ③拼成等腰梯形.
将所拼图形画在相应的网格中.
 |
① 拼成直角三角形
 |
|||
 |
|||
② 拼成平行四边形 ③ 拼成等腰梯形
(2) 能否将矩形ABCD剪 (限剪两刀) 拼成菱形?若能,请利用下面的网格设计剪拼图案(画出分割线即可)并写出相应的菱形的边长;若不能,请简要说明理由.
 |
21. 为了了解学生参加体育活动的情况,某中学对学生进行了随机抽样调查,其中一个问题是 “你平均每天参加体育活动的时间是多少?”,共有4个选项:
下图是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)在图①中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
 |
|||
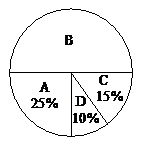 |
|||
图① 图②
解:
22.已知直线l1 :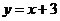 与 l2 :
与 l2 :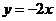 交于点B, 直线l1 与x轴交于点A, 动点P在线段OA上移动(不与点A、O重合) .
交于点B, 直线l1 与x轴交于点A, 动点P在线段OA上移动(不与点A、O重合) .
(1) 求点B的坐标;
(2) 过点P作直线l与x轴垂直, 设P点的横坐标为x, △ABO中位于直线l左侧部分的面积为S, 求S与x之间的函数关系式.
解:
得分
阅卷人
六、(本题满分7分)
23.如图,某学校要建一个中间有两道篱笆隔断的长方形花圃,花圃的一边靠墙(墙的最大可利用长度为
(1)求S与x之间的函数关系式;
(2)如果要围成面积为
(3)能围成面积比
 如果不能,请说明理由.
如果不能,请说明理由.
解:
得分
阅卷人
七、(本题满分8分)
24. 如图,在平面直角坐标系中,Rt△AOB的顶点坐标分别为A(-2,0),O(0,0),B(0,4),
把△AOB绕点O按顺时针方向旋转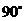 ,得到△COD.
,得到△COD.
(1)求C、D两点的坐标;
(2)求经过A、B、D三点的抛物线的解析式;
 (3)在(2)中的抛物线的对称轴上取两点E、F(点E在点F的上方),且EF=1,使四边形ACEF 的周长最小,求出E、F两点的坐标.
(3)在(2)中的抛物线的对称轴上取两点E、F(点E在点F的上方),且EF=1,使四边形ACEF 的周长最小,求出E、F两点的坐标.
解:
得分
阅卷人
八、(本题满分8分)
 25.在△ABC中,∠A、∠B、∠C所对的边分别用a、b、c表示。
25.在△ABC中,∠A、∠B、∠C所对的边分别用a、b、c表示。
(1)如图,在△ABC中,∠A=2∠B,且∠A=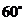 .
.
求证:a2=b(b+c).
证明:
(2)如果一个三角形的一个内角等于另一个内角的2 倍,我们称这样的三角形为“倍角三角形”.(1)中的三角形是一个特殊的倍角三角形,那么对于任意的倍角三角形ABC,其中∠A=2∠B,关系式a2=b(b+c)是否仍然成立?若成立,证明你的结论;若不成立,请说明理由.
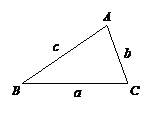 解:
解:
(3)试求出一个倍角三角形的三条边的长,使这三条边长恰为三个连续的正整数.
解: